初中数学3 探究三角形全等的条件说课ppt课件

这是一份初中数学3 探究三角形全等的条件说课ppt课件，共20页。PPT课件主要包含了“两边及夹角”，5cm，几何语言，必须是夹角，找相等边的方法，SAS，∵ADBC，∴∠A∠C，∵AECF，ADCB等内容，欢迎下载使用。
1. 探索并正确理解三角形全等的判定方法“SAS”，了解“SSA”不能作为两个三角形全等的条件；（重点）2. 会用“SAS”判定方法证明两个三角形全等及进行简单的应用.（难点）
对应相等的两个三角形全等，简写为 .
1.三角形全等的判定方法一（SSS）
“边边边”或“SSS”
两角及其 分别相等的两个三角形全等,简写成 .
2.三角形全等的判定方法二 （ASA）
两角分别相等且其中一组等角的 相等的两个三角形全等，简写成 .
3.三角形全等的判定方法三（AAS）
“角边角”或“ASA”
“角角边”或“AAS”
可以利用“ASA”画出.
还有没有其他方法呢？下面让我们一起继续探索三角形全等的条件吧！
小伟作业本上画的三角形被墨迹污染了，他想画一个与原来完全一样的三角形，他该怎么办？请你帮助小伟想一个办法，并说明你的理由．
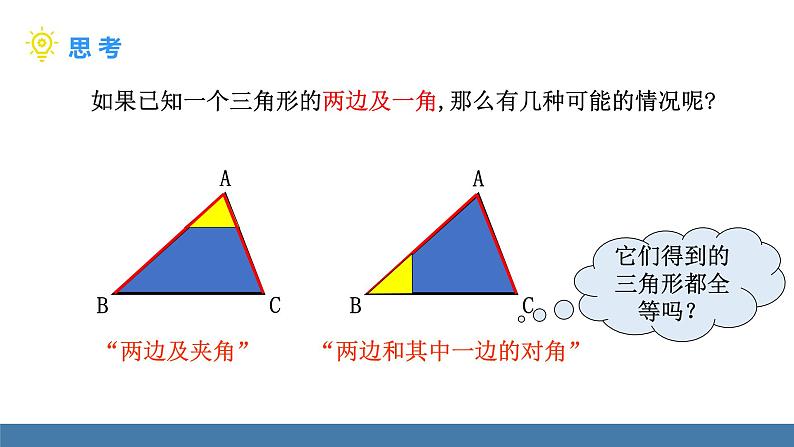
如果已知一个三角形的两边及一角,那么有几种可能的情况呢?
“两边和其中一边的对角”
它们得到的三角形都全等吗？
解:画的三角形都全等.改变条件中的角度和边长,画出的三角形也全等.
如果“两边及一角”条件中的角是两边的夹角,情况会怎样呢？小组合作，选择两条线段和一个角作为三角形的两边及其夹角，比如三角形两条边分别为2.5cm,3.5cm,它们所夹的角为40°,用尺规作出这个三角形.你作的三角形与同伴作的一定全等吗?
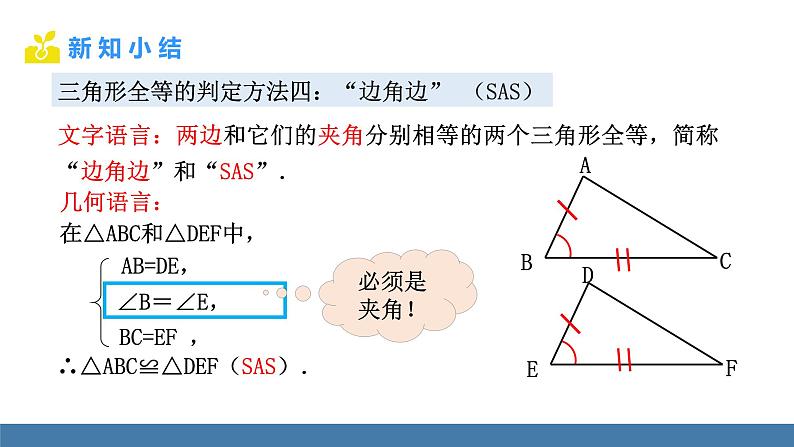
文字语言：两边和它们的夹角分别相等的两个三角形全等，简称“边角边”和“SAS”．
在△ABC和△DEF中，
∴△ABC≌△DEF（SAS）．
三角形全等的判定方法四：“边角边” （SAS）
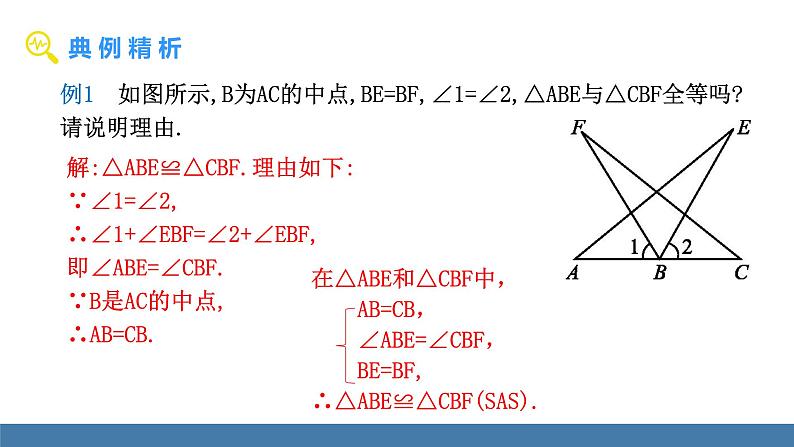
解:△ABE≌△CBF.理由如下:∵∠1=∠2,∴∠1+∠EBF=∠2+∠EBF,即∠ABE=∠CBF.∵B是AC的中点,∴AB=CB.
例1 如图所示,B为AC的中点,BE=BF,∠1=∠2,△ABE与△CBF全等吗?请说明理由.
在△ABE和△CBF中， AB=CB， ∠ABE=∠CBF， BE=BF,∴△ABE≌△CBF(SAS).
解析：要判断能不能使△ABC≌△DEF，应看所给出的条件是不是两边和这两边的夹角，只有选项C的条件不符合，故选C.
1.下列条件中，不能证明△ABC≌△DEF的是(　　)
A．AB＝DE，∠B＝∠E，BC＝EFB．AB＝DE，∠A＝∠D，AC＝DFC．BC＝EF，∠B＝∠E，AC＝DFD．BC＝EF，∠C＝∠F，AC＝DF
如图，已知线段a，c，∠α，用尺规作△ABC，使BC=a，AB=c，∠ABC=∠α．
回顾上述作图过程，请你总结“已知三角形的两边及其夹角，用尺规作这个三角形”的方法和步骤.
（1）作一条线段BC=a.
（2）以点B为顶点，以BC为一边，作角∠DBC=∠α.
（3）在射线BD上截取线段BA=c；
（4）连接AC.△ABC就是所要作的三角形．
如果“两边及一角”条件中的角是其中一边的对角，情况会怎样呢? 如图，已知△ABC的AB边和边长为 l 的AC边，以及AC边的对角∠B，你能用尺规确定顶点C的位置吗?把你作的三角形与同伴作的进行比较，由此你发现了什么？与同伴进行交流.
结论：两边分别相等且其中一组等边的对角相等的两个三角形不一定全等.
△ABC与△A1B1C1均符合条件，但不全等.
解：在△ODC和△OBA中，
∴△ODC≌△OBA(SAS)．∴∠C＝∠A(全等三角形的对应角相等)，∴DC∥AB(内错角相等，两直线平行)．
2.如图，AC和BD相交于点O，OA＝OC，OB＝OD.试说明：DC∥AB.
OD=OB(已知)∠DOC=∠BOA(对顶角相等)OC=OA(已知)
1.公共边；2.等线段加(减)同线段其和(差)相等（等式的性质）；3.由中点得到线段相等；4.全等三角形的对应边相等.
1.下列与图1三角形全等的是（    ）A．①②B．②③C．①③D．只有①
2.如图所示，有以下4个等式:(1)∠BCA=∠DCA;(2)AB=AD；(3)∠BAC=∠DAC;(4)BC=DC.以其中的2个等式为依据不能判定△ABC≌△ADC的是(　　)A.(1)(2) B.(1)(3) C.(1)(4) D.(2)(3)
答案不唯一,如∠ACB=∠DCE或AB=DE
3.如图，AB⊥CF,垂足为B,AB∥DE,点E在CF上,CE=FB, AB=DE,依据以上条件可以判定△ABC≌△DEF,这种判定三角形全等的方法可以简写为　　　. 
4.如图所示，已知AC=DC,BC=EC,请你添加一个适当的条件:　　　　 ,使得△ABC≌ △DEC. 
5.如图，点E、F在AC上，AD//BC，AD=CB，AE=CF.试说明：△AFD≌△CEB.
∴AE+EF=CF+EF， 即 AF=CE.
在△AFD和△CEB中，
∴△AFD≌△CEB（SAS）.