




所属成套资源:北师大版(2024)数学七年级下册同步教学课件
初中数学北师大版(2024)七年级下册(2024)4 利用三角形全等测距离课文内容ppt课件
展开
这是一份初中数学北师大版(2024)七年级下册(2024)4 利用三角形全等测距离课文内容ppt课件,共21页。PPT课件主要包含了方便测量的线段,方案一,方案二,所以ACBD等内容,欢迎下载使用。
判定三角形全等有哪些方法?
①“SSS”:三边对应相等的两个三角形全等。
②“ASA”:两角和它们的夹边对应相等的两个三角形全等。
③“AAS”:两角和其中一角的对边对应相等的两个三角形全等。
④“SAS”:两边和它们的夹角对应相等的两个三角形全等。
“调整帽子”“保持刚才的姿态”的数学意义是什么?
“调整帽子”即可改变视角的大小。帽檐向上移动,视角变大,观察到的范围变大;帽檐向下移动,视角变小,观察到的范围变小。
“保持刚才的姿态”即保持视角不变。
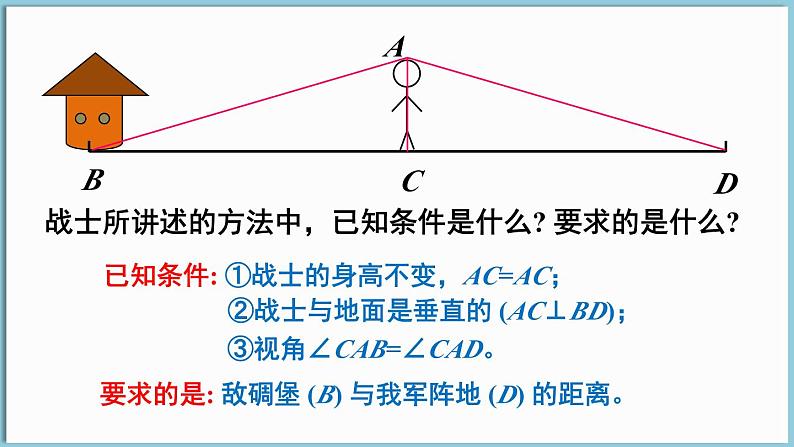
战士所讲述的方法中,已知条件是什么? 要求的是什么?
已知条件: ①战士的身高不变,AC=AC;
②战士与地面是垂直的 (AC⊥BD);
③视角∠CAB=∠CAD。
要求的是: 敌碉堡 (B) 与我军阵地 (D) 的距离。
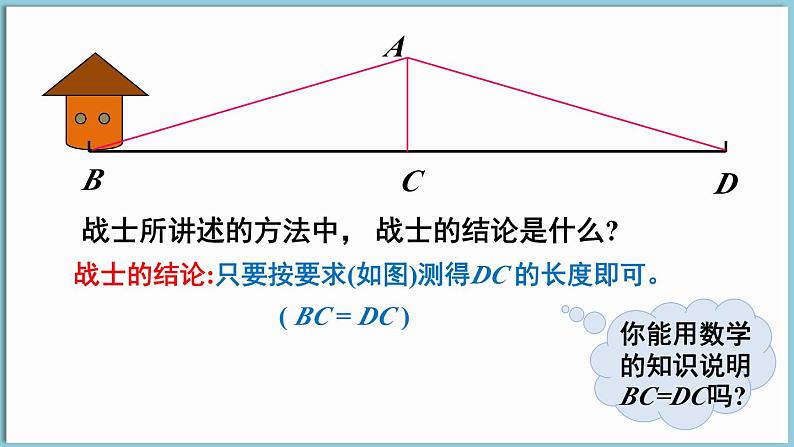
战士所讲述的方法中, 战士的结论是什么?
战士的结论:只要按要求(如图)测得DC 的长度即可。 ( BC = DC )
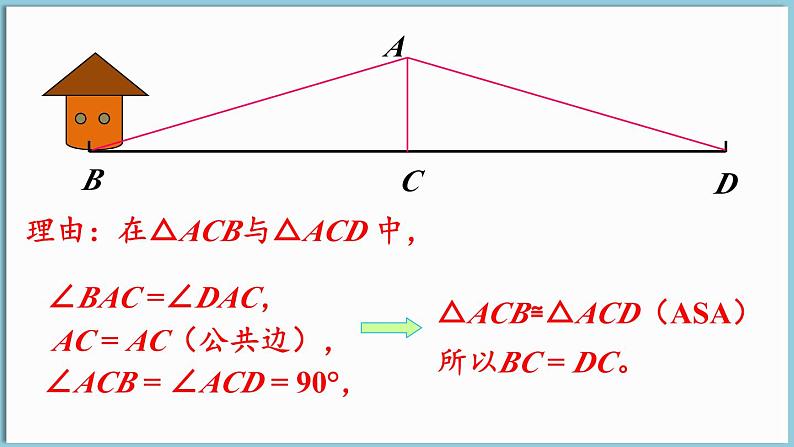
理由:在△ACB与△ACD 中,
△ACB≌△ACD(ASA)
所以BC = DC。
利用三角形全等可以测量两点之间的距离。
不可测量或不方便测量的线段
利用全等三角形的性质转移线段。
如图,A,B两点分别位于一个池塘的两端,小丽想用绳子测量A,B间的距离,但绳子不够长,你能帮小丽设计一个方案,解决问题吗?
先在地上取一个可以直接到达 A 和 B 点的点 C;
连接 AC 并延长到 D,使CD = CA;连接 BC 并延长到E,使 CE = CB,
连接 DE 并测量出它的长度即为AB 之间的距离.
理由: 在△ACB与△DCE 中,
所以△ACB ≌ △DCE(SAS)
所以 AB = DE
(全等三角形的对应边相等)
理由: 在△DAC与△BCA 中,
所以△DAC ≌ △BCA(SAS)
所以 AB = CD
1.如图,把两根钢条 AB,CD的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳 )。 只要量得 AC 的长度,就可知工件的内径 BD 是否符合标准。你明白其中的道理吗?与同伴进行交流。
【课本P111 随堂练习 第1题】
解:因为点O是AB,CD的中点,
所以点AO=BO,CO=DO。
又因为在△AOC和△BOD中,
所以 △AOC≌△BOD (SAS)
AO = BO,∠AOC =∠BOC,CO=DO ,
1. 如图所示小明设计了一种测工件内径AB的卡钳, 问:在卡钳的设计中,AO、BO、CO、DO 应 满足下列的哪个条件?( ) A. AO = CO B. BO = DO C. AC = BD D. AO = CO 且 BO = DO
2.如图要测量河两岸相对的两点 A、B 的距离,先在AB 的垂线 BF 上取两点 C、D,使CD = BC,再定出 BF 的垂线 DE,可以证明△EDC ≌ △ABC,得ED = AB,因此,测得 ED 的长就是 AB 的长. 判定 △EDC ≌ △ABC 的理由是 ( ) A. SSS B. ASA C. AAS D. SAS
3. 池塘两边有 A,B 两点,想知道 A,B 两点间 的距离,但又无法直接测量,于是有人想出办 法,利用三角形全等解决这个问题,但是在三 角形全等的判断方法中,不能采用的是( ). A. SAS B. ASA C. AAS D. SSS
4.如图,在新修的小区中,有一条“Z”字形绿色长廊ABCD,其中AB//CD,在AB,BC,CD 三段绿色长廊上各修一小凉亭E,M,F,且BE=CF,M是 BC 的中点,在凉亭M与F之间有一池塘,不能直接到达,如何测出凉亭M与F之间的距离?请说明理由。
解:如图,连接 ME,MF。因为 AB//CD,所以∠B=∠C。因为M是BC 的中点,所以BM=CM。又因为在△MEB和△MFC 中,BE=CF,∠B=∠C,BM=CM,所以△MEB≌△MFC (SAS),所以 ME=MF。所以测出凉亭M与E之间的距离,便可得到凉亭M与F之间的距离。
相关课件
这是一份数学第四章 三角形4 利用三角形全等测距离背景图ppt课件,共30页。PPT课件主要包含了所以DEAB,说一说其中的道理,所以APCD,利用全等三角形测距离,数学思想,请完成第1~2题,基础题,测量池塘的宽度,拓展提升等内容,欢迎下载使用。
这是一份初中数学北师大版(2024)七年级下册(2024)第四章 三角形4 利用三角形全等测距离说课ppt课件,共14页。PPT课件主要包含了学习目标,新课导入,新知探究,方便测量的线段,构造全等三角形,课堂小结,课堂训练,SAS等内容,欢迎下载使用。
这是一份北师大版(2024)七年级下册(2024)4 利用三角形全等测距离教案配套课件ppt,共16页。PPT课件主要包含了探索三角形全等的条件,边角边角角边,边角边,利用三角形全等测距离,延长法构造全等三角形,垂直法构造全等三角形,数学思想等内容,欢迎下载使用。










