初中数学北师大版（2024）七年级下册（2024）3 探究三角形全等的条件教学演示课件ppt

这是一份初中数学北师大版（2024）七年级下册（2024）3 探究三角形全等的条件教学演示课件ppt，共22页。PPT课件主要包含了学习目标，新课导入，新知探究，不一定全等，做一做，课堂小结，课堂训练，ABDC，三角形具有稳定性等内容，欢迎下载使用。
1．了解三角形的稳定性，会应用“边边边”判定两个三角形全等。【重点】2．经历探索“边边边”判定三角形全等的过程，体会利用操作、归纳获得数学结论的过程。【重点】3．在复杂的图形中进行三角形全等条件的分析和探索。【难点】4．已知三边会作三角形。【重点，难点】
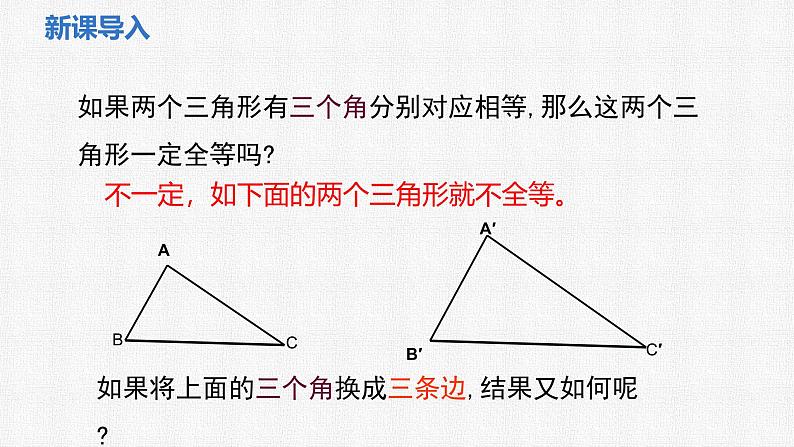
如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
不一定，如下面的两个三角形就不全等。
如果将上面的三个角换成三条边,结果又如何呢?
知识点 三角形全等的判定“SSS”
1.只给一个条件(一条边或一个角)画三角形时，大家画出的三角形一定全等吗？
2.给出两个条件画三角形时，有几种可能的情况？每种情况下作出的三角形一定全等吗？分别按照下面的条件做一做。（1）三角形的一个内角为30°，一条边为3cm；（2）三角形的两个内角分别为30°和50°；（3）三角形的两条边分别为4cm，6cm。
发现：只给出一个或两个条件时，都不能保证所画的三角形一定全等。
已知一个三角形的三条边分别为4cm，5cm和7cm，你能画出这个三角形吗？把你画的三角形与同伴画出的进行比较，它们一定全等吗？
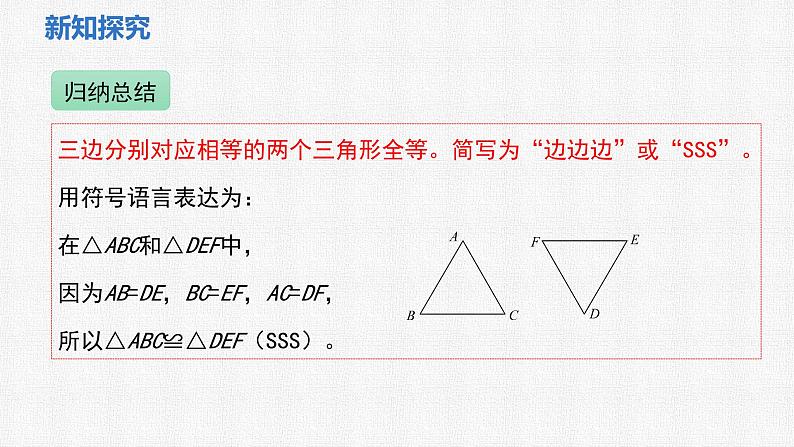
三边分别对应相等的两个三角形全等。简写为“边边边”或“SSS”。用符号语言表达为：在△ABC和△DEF中，因为AB=DE，BC=EF，AC=DF，所以△ABC≌△DEF（SSS）。
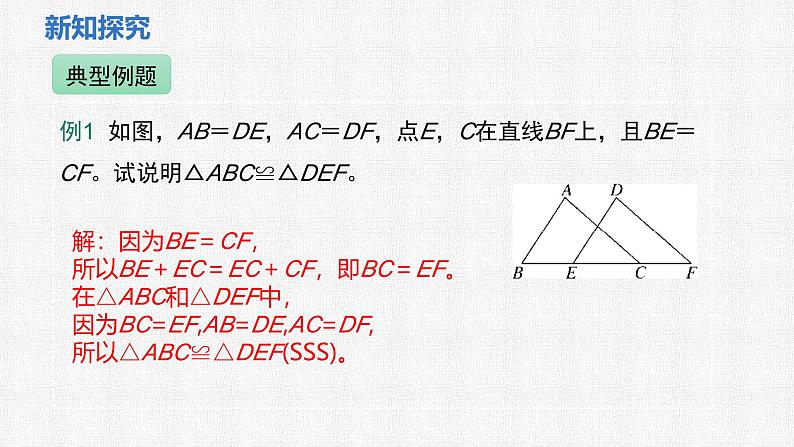
例1 如图，AB＝DE，AC＝DF，点E，C在直线BF上，且BE＝CF。试说明△ABC≌△DEF。　
解：因为BE＝CF，所以BE＋EC＝EC＋CF，即BC＝EF。在△ABC和△DEF中，因为BC=EF,AB=DE,AC=DF,所以△ABC≌△DEF(SSS)。
方法总结：常见的隐含的等边有：①公共边相等；②等边加（减）等边，其和（或差）仍相等；③由三角形中线的定义得出线段相等；④全等三角形的对应边相等。
如图所示，△ABC是一个风筝架，AB＝AC，AD是连接点A与BC中点D的支架。试说明AD⊥BC。
解：因为D是BC的中点，所以BD＝CD。在△ABD和△ACD中，因为AB=AC,BD=CD,AD=AD,所以△ABD≌△ACD(SSS)，所以∠1＝∠2。因为∠1＋∠2＝180°，所以∠1＝∠2＝90°，所以AD⊥BC。
知识点 已知三边用尺规作三角形
例2 已知三条线段a,b,c，用尺规作出△ABC，使BC＝a，AC＝b，AB＝c。
解：作法：(1)作线段BC＝a； (2)以点C为圆心，以b的长为半径画弧，再以点B为圆心，以c的长为半径画弧，两弧相交于点A； (3)连接AC和AB，则△ABC即为所求作的三角形，如图所示。
方法总结：已知三角形三边的长，根据全等三角形的判定“SSS”，所作三角形的形状和大小也就确定了。
知识点 三角形的稳定性
三角形具有稳定性，四边形具有不稳定性。
取三根长度适当的木条，用钉子钉成一个三角形的框架，你所得到的框架的形状固定吗？用四根木条钉成的框架的形状固定吗？
例3 生活中，我们经常看到在电线杆上拉两根钢缆来对其加固，如图所示，这是利用了三角形的 (　 　) A．稳定性 B．全等性 C．灵活性 D．对称性
1.三边分别对应相等的两个三角形全等。简写为“边边边”或“SSS”。2.已知三边作三角形。3.三角形具有稳定性。
1．如图，已知AC＝BD，要使得△ABC≌△DCB，只需增加的一个与边有关的条件是 。2. 如图，在△ABC中，AB＝BE，AD＝DE，∠A＝80°，则∠CED＝ 。
3.一扇窗户打开后，用窗钩将其固定，运用的原理是： ；要使四边形木架不变形，至少要再钉上 根木条，要使六边形木架不变形，至少再钉下 根木条。
4.已知，如图，在四边形ABCD中，AB＝CB，AD＝CD。试说明∠C＝∠A。
解：连接DB，在△DCB和△DAB中，因为AB＝CB，AD＝CD，DB＝DB，所以△DCB≌△DAB(SSS)，所以∠C＝∠A。
5.如图，AD＝CB，E，F是AC上两动点，且有DE＝BF。(1)若点E，F运动至图①所示的位置，且有AF＝CE。试说明△ADE≌△CBF。
解：因为AF＝CE，所以AF＋EF＝CE＋EF，所以AE＝CF。在△ADE和△CBF中，因为AD=CB,DE=BF,AE=CF。所以△ADE≌△CBF(SSS)。
(2)若点E，F运动至图②所示的位置，仍有AF＝CE，那么△ADE≌△CBF还成立吗？为什么？
解：成立。因为AF＝CE，所以AF－EF＝CE－EF，所以AE＝CF。在△ADE和△CBF中，因为AD=CB,DE=BF,AE=CF,所以△ADE≌△CBF(SSS)。