初中3 探究三角形全等的条件图片ppt课件

这是一份初中3 探究三角形全等的条件图片ppt课件，共27页。PPT课件主要包含了学习目标，新课导入，新知探究，“两边及夹角”，做一做，几何语言，课堂小结，课堂训练，20°，第四章三角形等内容，欢迎下载使用。
1.理解并掌握三角形全等的判定方法——“边角边”。【重点】2.已知两边及其夹角会作三角形。【难点】
小伟作业本上画的三角形被墨迹污染了，他想画一个与原来完全一样的三角形，他该怎么办？请你帮助小伟想一个办法，并说明你的理由。
要画一个三角形与小伟画的三角形全等，需要几个与边或角的大小有关的条件？
知识点 三角形全等的条件——“SAS”
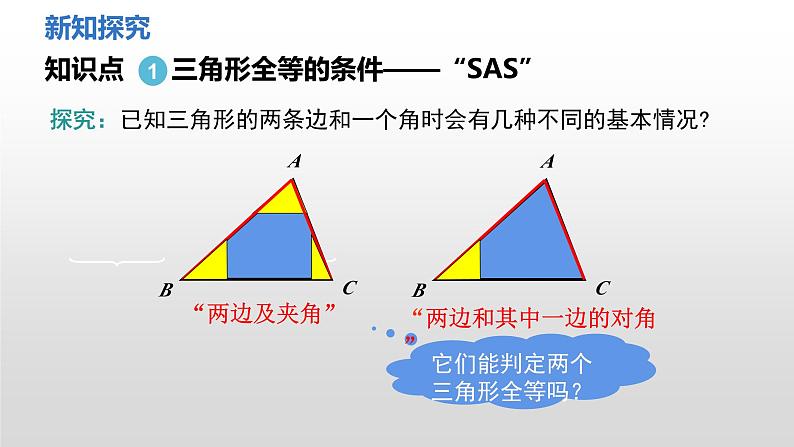
已知三角形的两条边和一个角时会有几种不同的基本情况?
它们能判定两个三角形全等吗？
“两边和其中一边的对角”
如果“两边及一角”条件中的角是两边的夹角，比如三角形两条边分别为 2cm，3 cm，它们所夹的角为 40°，你能画出这个三角形吗？
将你所画的三角形剪下来，和其他同学剪的三角形比较，它们能够重合吗？
三角形全等的条件——“SAS”
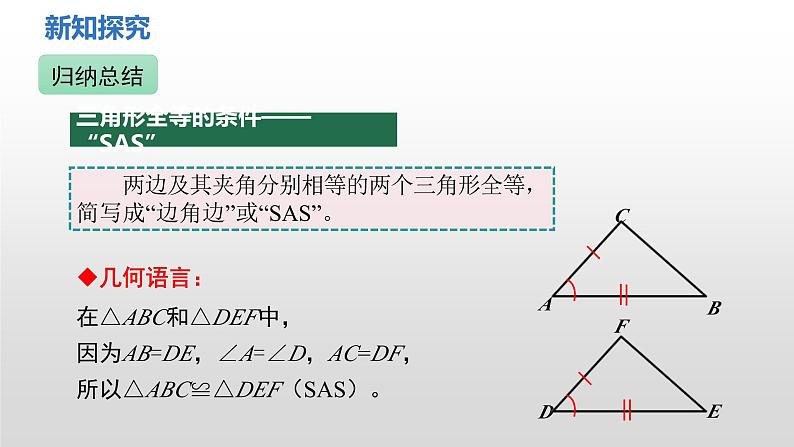
两边及其夹角分别相等的两个三角形全等，简写成“边角边”或“SAS”。
在△ABC和△DEF中，因为AB=DE，∠A=∠D，AC=DF，所以△ABC≌△DEF（SAS）。
例1 如图，A，D，F，B在同一直线上，AD＝BF，AE＝BC，且AE∥BC。试说明：△AEF≌△BCD。
解：因为AE∥BC，所以∠A＝∠B。因为AD＝BF，所以AF＝BD。在△AEF和△BCD中，因为AE=BC，∠A=∠B，AF=BD，所以△AEF≌△BCD(SAS)。
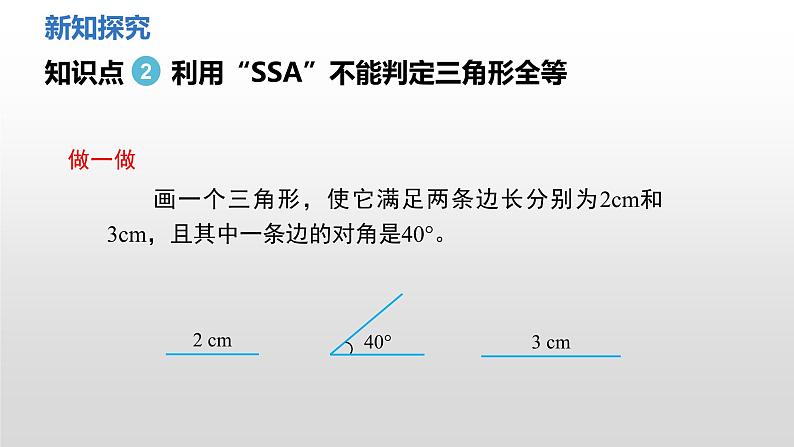
知识点 利用“SSA”不能判定三角形全等
画一个三角形，使它满足两条边长分别为2cm和3cm，且其中一条边的对角是40°。
两边分别相等且其中一组等边的对角分别相等的两个三角形不一定全等，即“SSA”不能判定两个三角形全等。
下列条件中，不能判定△ABC≌△DEF的是(　　)
A．AB＝DE，∠B＝∠E，BC＝EFB．AB＝DE，∠A＝∠D，AC＝DFC．BC＝EF，∠B＝∠E，AC＝DFD．BC＝EF，∠C＝∠F，AC＝DF
解析：要判断能不能使△ABC≌△DEF，应看所给出的条件是不是两边和这两边的夹角，只有选项C的条件不符合。故选C。
例2 如图，已知∠α和线段m，n。求作△ABC，使∠B＝∠α，BA＝n，BC＝m。
知识点 已知两边及其夹角用尺规作三角形
解：作法：(1)作一条线段BC＝m；(2)以B为顶点，以BC为一边，作∠DBC＝∠α；(3)在射线BD上截取线段BA＝n；(4)连接AC，△ABC就是所求作的三角形。
有两边及夹角对应相等的两个三角形全等（简写成 “SAS”)
为证明线段和角相等提供了新的证法
1.已知两边，必须找“夹角”2. 已知一角和这角的一夹边，必须找这角的另一夹边
已知两边及其夹角作三角形
1.如图，在△ABC和△DEF中，已知AB=DE，BC=EF，根据SAS 判 定△ABC≌△DEF，还需的条件是（ ）    
A.∠A=∠D       B.∠B=∠E       C.∠C=∠F       D.以上三个均可以
2.如图，AD=AE，BE=CD，∠1=∠2=110°,∠BAE=60°,则∠CAE= 。
3.如图，已知在△ABC中，AB=AC，∠1=∠2。试判断AD与BC，BD 与DC的关系并说明理由。
解：在△ABD和△ACD中，因为AB=AC，∠1=∠2，AD=AD，所以△ABD≌△ACD（SAS）。所以BD=CD，∠3=∠4。又因为∠3+∠4=180°，即2∠3=180°，所以∠3=90°。所以AD⊥BC。 
4. 如图，BC∥EF，BC＝BE，AB＝FB，∠1＝∠2，若∠1＝60°，求 ∠C的度数。
解：因为∠1＝∠2，所以∠ABC＝∠FBE。在△ABC和△FBE中，因为BC=BE，∠ABC=∠FBE，AB=FB，所以△ABC≌△FBE(SAS)。所以∠C＝∠BEF。又因为BC∥EF，所以∠C＝∠BEF＝∠1＝60°。
3　探索三角形全等的条件
北师大版-数学-七年级下册
第4课时　灵活选择方法判定三角形全等
1.能够灵活选择合适的三角形全等的判定方法判定三角形全等。【重点】2.能够运用三角形的判定和全等三角形的性质进行合情推理。【难点】
到目前为止，我们学过的可以作为判定两个三角形全等的方法有几种？
1. 三角形全等的定义2. SSS——三边分别相等3. ASA——两角及其夹边分别相等4. AAS——两角分别相等且其中一组等角的对边相等5. SAS——两边及其夹角分别相等
知识点 灵活选择方法判定三角形全等
例1 如图，∠B＝∠DEF，BC＝EF,补充条件说明：△ABC≌△DEF。(1)若要以“SAS”为依据，还缺条件 ；(2)若要以“ASA”为依据，还缺条件 ； (3)若要以“AAS”为依据，还缺条件 ；(4)若要以“SSS” 为依据，还缺条件 。
AB=DE，AC=DF
找另一个邻角(ASA)
找角的另一个边(SAS)
找这边的对角(AAS)
找另外一个角(AAS)
找夹边外的任意边(AAS)
1.如图，已知AD＝AE，下列条件中，不能使△ADB≌△AEC的是(　　)
2.如图，△ABC的两条高AD，BE相交于点F，请添加 一个条件，使得 △ADC≌△BEC(不添加其他字母 及辅助线)，你添加的条件是　 　 。
A.∠B＝∠C B.∠AEC＝∠ADB   C.AB＝AC D.CE＝BD
例2 已知：如图，AB＝ CD，BC ＝ DA，E，F是 AC 上的两点，且 AE ＝ CF。试说明：BF ＝ DE。
解：在△ABC和△CDA中，因为AB=CD，BC=DA，CA=AC，所以△ABC≌△CDA。(SSS)所以∠1＝∠2。在△BCF与△DAE中，因为BC=DA，∠1=∠2，CF=AE，所以△BCF≌△DAE。(SAS)所以BF＝DE。
所要说明的边或角所在的两个三角形不能直接判定全等时，需要先根据条件判定另外两个三角形全等后，得出条件再说明它们全等。
如图，在四边形ABCD中，AB＝AD，BC＝DC，E为AC上的一动点(不与A重合)，在点E移动过程中BE和DE是否相等？若相等，请写出说明过程；若不相等，请说明理由。
解：相等。理由如下：在△ABC和△ADC中，因为AB＝AD，AC＝AC，BC＝DC，所以△ABC≌△ADC(SSS)。所以∠DAE＝∠BAE。在△ADE和△ABE中，因为AB＝AD，∠DAE＝∠BAE，AE＝AE，所以△ADE≌△ABE(SAS)。所以BE＝DE。
1.如图，已知AB＝DC，下列所给的条件不能证明△ABC≌△DCB的是(　　)A．AC＝BD  B．∠ABC＝∠DCB      C．∠A＝∠D  D．∠ACB＝∠DBC2.根据下列条件，能作出唯一的△ABC的是(　　)A．AB＝3，BC＝4，AC＝8B．AB＝4，BC＝3，∠A＝30°C．∠A＝60°，∠B＝45°，AB＝4D．∠C＝90°，AB＝6