北师大版（2024）七年级下册（2024）第四章 三角形3 探究三角形全等的条件教案配套课件ppt

这是一份北师大版（2024）七年级下册（2024）第四章 三角形3 探究三角形全等的条件教案配套课件ppt，共19页。PPT课件主要包含了几何语言，SSS，①两角及夹边，解全等理由，第1块，所以∠C的度数可求，∠A∠B以及AC，∠A∠C以及AC，ASA，△DCO等内容，欢迎下载使用。
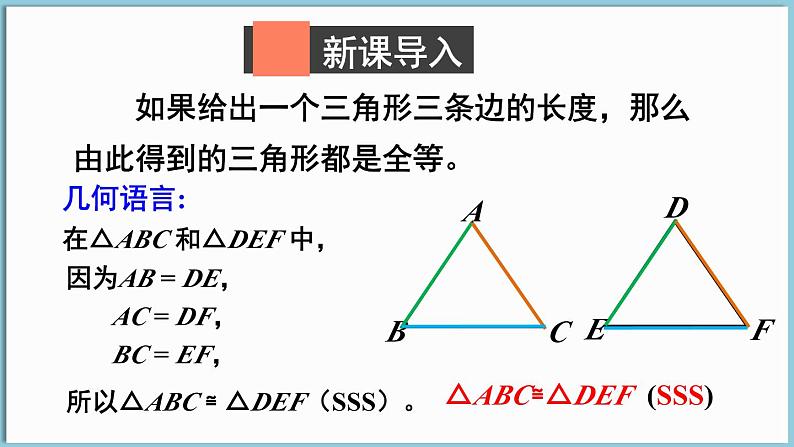
如果给出一个三角形三条边的长度，那么由此得到的三角形都是全等。
△ABC≌△DEF (SSS)
在△ABC 和△DEF 中，
因为AB = DE， AC = DF， BC = EF，
所以△ABC ≌ △DEF（SSS）。
当两个三角形满足六个条件中的三个时，有四种情况:
探究点1：“角边角”判定三角形全等
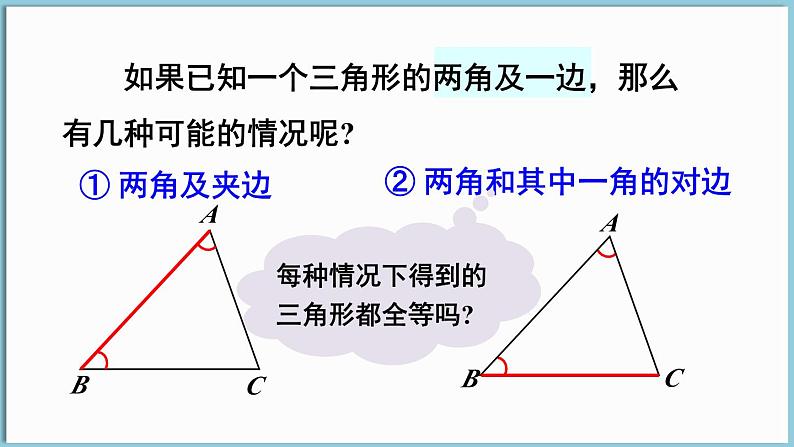
如果已知一个三角形的两角及一边，那么有几种可能的情况呢?
② 两角和其中一角的对边
如果“两角及一边”条件中的边是两角所夹的边，情况会怎样呢？
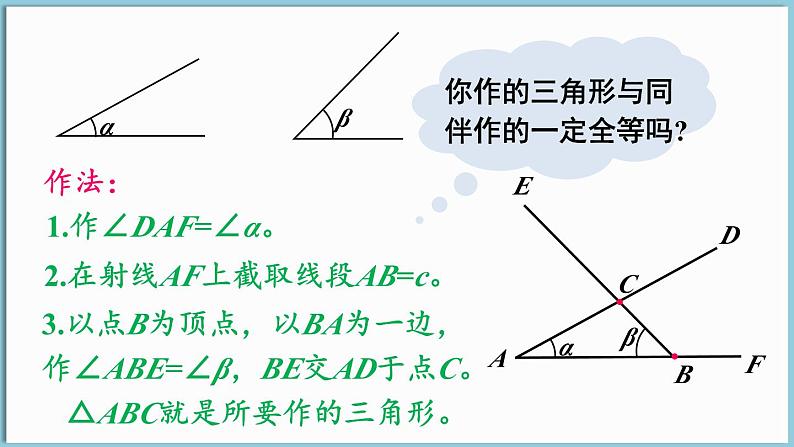
如图，已知∠α，∠β，线段c，用尺规作△ABC，使∠A=∠α，∠B=∠β，AB=c。
1.作∠DAF=∠α。
2.在射线AF上截取线段AB=c。
3.以点B为顶点，以BA为一边，作∠ABE=∠β，BE交AD于点C。
△ABC就是所要作的三角形。
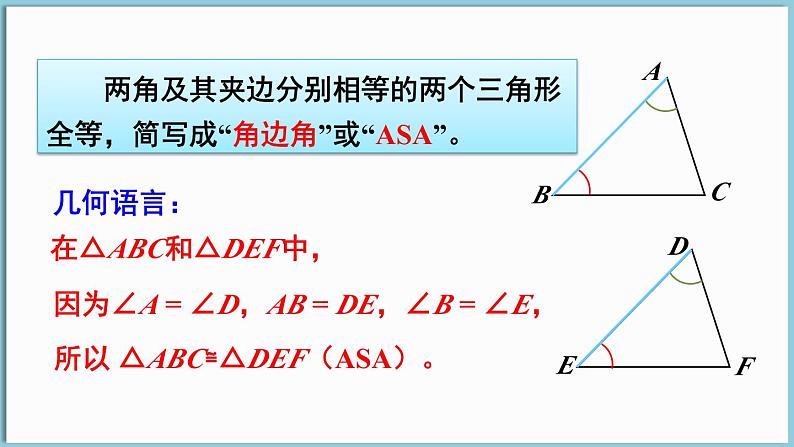
在△ABC和△DEF中，
因为∠A = ∠D，AB = DE，∠B = ∠E，
所以 △ABC≌△DEF（ASA）。
两角及其夹边分别相等的两个三角形全等，简写成“角边角”或“ASA”。
注意：书写两个三角形全等的条件“ASA”时，一定要把夹边相等写在中间，以突出角边角的位置以及对应关系.
1.如图，AB与CD相交于点O，O是AB的中点，∠A=∠B，△AOC与△BOD全等吗? 为什么?
所以 △AOC ≌ △BOD（ASA）。
因为 O是 AB 中点，所以 OA = OB。又因为∠A = ∠B，∠AOC = ∠BOD，
【课本P102 随堂练习 第1题】
2. 莉莉不慎将一块三角形玻璃打碎为三块，她是否可以只带其中的一块碎片到商店去，就能配一块与原来一样的三角形玻璃吗?如果可以，带哪块去合适?
如果“两角及一边”条件中的边是其中一角的对边，情况会怎样呢?
如图所示，已知∠A，∠B以及AC。
因为三角形内角和为180°，
探究点2：利用“角角边”判定三角形全等
因为∠B = ∠E，∠A = ∠D，AC = DF，
所以△ABC≌△DEF（AAS）。
两角分别相等且其中一组等角的对边相等的两个三角形全等，简写成“角角边”或“AAS”。
如图，已知∠A =∠D，AB = CD，可得△ABO≌_______，理由是______。
1. 如图，已知∠A =∠D，∠1 = ∠2，那么要得到△ABC ≌ △DEF，还应给出的条件是（ ） A.∠E =∠B B.ED = BC C.AB = EF D.AF = CD
2. 如图，D 是 AB 上一点，DF 交 AC 于点E，DE=FE ，FC∥AB。若AB=4，CF=3，则 BD的长是( )
3. 如图，点 A，B，C，D 在同一条直线上，BE//DF，∠A=∠F，AB=FD。 试说明：AE=FC。
解：因为BE // DF，所以∠ABE = ∠D。
又因为 AB = FD，∠A = ∠F，
所以 △ABE ≌ △FDC（ASA）
所以 AE = FC。
4. 如图，AB=AE，∠1=∠2，∠C=∠D.试说明：△ABC ≌ △AED。
解：理由如下：因为∠1=∠2，所以∠1+∠EAC =∠2+∠EAC，即∠BAC = ∠EAD。
又因为∠C = ∠D，AB = AE，
所以 △ABC ≌ △AED （AAS）.
5.如图，∠E=∠F=90°， ∠ B= ∠ C，AE=AF。请你判断△ACN≌△ABM 是否成立，并说明理由。
解：成立。理由如下：在△AEB和△AFC中，因为∠B=∠C，∠E=∠F，AE=AF，所以△AEB≌△AFC (AAS)。所以AB=AC。在△ACN和△ABM中，因为∠CAN=∠BAM，AC=AB，∠C=∠B，所以△ ACN≌△ABM (ASA)。