北师大版（2024）七年级下册（2024）3 探究三角形全等的条件教课内容课件ppt

这是一份北师大版（2024）七年级下册（2024）3 探究三角形全等的条件教课内容课件ppt，共40页。
1. 掌握三角形全等的“边边边”判定条件，了解三角形的稳定性.2. 会根据三边长作三角形，初步运用“边边边”条件有条理地思考并进行简单推理.
要画一个三角形，使它与小明画的三角形全等，你会怎么画呢?
想一想，动手画一画吧！
要画一个与已知三角形全等的三角形，至少需要几个与边或角的大小有关的条件?
我猜测至少需要三个与边或角的大小有关的条件.
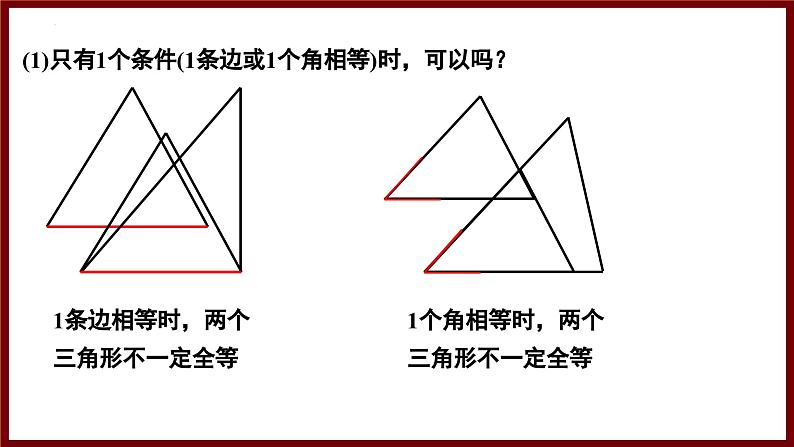
(1)只有1个条件(1条边或1个角相等)时，可以吗？
1条边相等时，两个三角形不一定全等
1个角相等时，两个三角形不一定全等
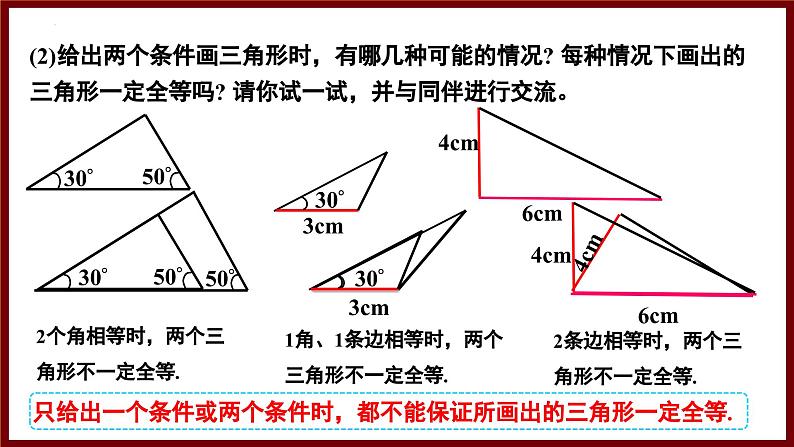
(2)给出两个条件画三角形时，有哪几种可能的情况? 每种情况下画出的三角形一定全等吗? 请你试一试，并与同伴进行交流。
2个角相等时，两个三角形不一定全等.
1角、1条边相等时，两个三角形不一定全等.
2条边相等时，两个三角形不一定全等.
给出三个条件画三角形，有哪几种可能的情况？与同伴进行交流.
(3)两边和一角相等；
(4)两角和一边相等.
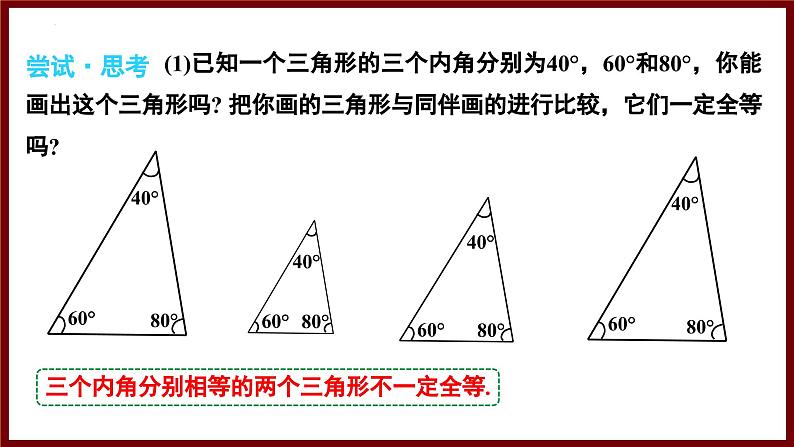
(1)已知一个三角形的三个内角分别为40°，60°和80°，你能画出这个三角形吗? 把你画的三角形与同伴画的进行比较，它们一定全等吗?
(2)已知一个三角形的三条边分别为4 cm，5cm和7cm，你能画出这个三角形吗? 把你画的三角形与同伴画的进行比较，它们一定全等吗?
情况(3)两边和一角相等和情况(4)两角和一边相等，下节课讨论！
(3)小组合作，选择三条线段作为三角形的三条边，并用尺规作出这个三角形. 把你作的三角形与同伴作的进行比较，它们一定全等吗?
如图，已知线段a，b，c，用尺规作△ABC，使AB=c，AC=b，BC=a.
②分别以点B，C为圆心，以c，b的长为半径作弧，两弧交于点A.
①作一条线段BC=a.
③连接AB，AC.△ABC就是所要作的三角形.
在△ABC和△ DEF中，
所以 △ABC ≌△ DEF (SSS).
因为AB=DE，BC=EF，CA=FD，
三边分别相等的两个三角形全等，简写为“边边边”或“SSS”.
例 如图， C是BF的中点，AB =DC，AC=DF. 试说明: △ABC ≌△DCF.
解：因为C是BF中点， 所以BC=CF. 在△ABC 和△DCF中， 因为AB = DC，AC = DF，BC = CF， 所以 △ABC ≌ △DCF(SSS).
用小木条分别钉成一个三角形和四边形的框架，用力转动某一个支点，框架的形状会发生改变吗？
三角形的大小和形状是固定不变的，这个性质叫作三角形的稳定性；四边形的形状是可以改变的，四边形具有不稳定性.
小明在钉成四边形框架的基础上，把对角又用一根木条钉起来了(如图)，此时这个四边形是否具有稳定性？
此时的框架相当于两个三角形拼在一起，同样具有稳定性.
三角形的稳定性(1)如果三角形的三边长确定，这个三角形的形状、大小就完全确定了，三角形的这种性质叫作三角形的稳定性.(2)四边形及四边以上的图形，形状是可以改变的，因此具有不稳定性.
在生活中，我们经常会看到应用三角形稳定性的例子.
你还能举出其他例子吗？
1. 如图，桥梁的斜拉钢索是三角形的结构，主要是为了 ( )
A.节省材料，节约成本 B.保持对称 C.利用三角形的稳定性 D.美观漂亮
2. 如图，AB＝CD，AD＝BC，则下列结论： ①△ABC≌△CDB；②△ABC≌△CDA；③△ABD ≌△CDB；④ BA∥DC. 正确的个数是 ( ) A. 1 B. 2 C. 3 D. 4
解：(1)因为AD＝BE，所以AD＋DB＝BE＋DB，即AB＝DE，因为AC＝DF，BC＝EF，所以△ABC≌△DEF；
3.(2024内江)如图，点A、D、B、E在同一条直线上，AD＝BE，AC＝DF，BC＝EF. (1)试说明：△ABC≌△DEF；
(2)因为△ABC≌△DEF，∠A＝55°，所以∠A＝∠FDE＝55°，因为∠E＝45°，所以∠F＝180°－∠FDE－∠E＝80°.
3.(2024内江)如图，点A、D、B、E在同一条直线上，AD＝BE，AC＝DF，BC＝EF (2)若∠A＝55°，∠E＝45°，求∠F的度数．
4.如图，仪器ABCD可以用来平分一个角，其中AB=AD，BC=DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们落在角的两边上，沿AC画一条射线AE，AE就是∠PRQ的平分线. 你能说明其中的道理吗？
解：在△ABC和△ADC中，因为AB=AD，BC=DC，AC=AC，所以△ABC≌△ADC(SSS).所以∠BAC=∠DAC，即∠QRE=∠PRE故AE就是∠PRQ的平分线.
(全等三角形的对应角相等)
利用“边边边”判定三角形全等
如果三角形的三边长确定，这个三角形的形状、大小就完全确定了，三角形的这种性质叫作三角形的稳定性.
知识点1　用“SSS”判定三角形全等
1. 如图，已知△ABC，则甲、乙、丙三个三角形中与△ABC全等的是 (　B　)
2. 如图，AB＝AD，BE＝DE，BC＝DC，则图中全等三角形有 (　B　)
第2题图
3. (教材复习题第6题改编)3．1　根据全等添加条件如图，AB＝ED，C是BD边的中点，若添加一个条件，可用“SSS”判定 △ABC≌△EDC，这个条件是 ___________.
3．2　改变图形位置说明全等如图，AE＝BF，AC＝DE，BC＝DF，试说明：△ABC≌△EFD.
知识点2　已知三边用尺规作三角形
4. (教材复习题第13题改编)数学课上，小明用直尺和圆规作一个角等于已 知角，如图，可得到△OCD≌△O′C′D′，则小明得到全等的依据是 ____________________________________．
SSS（三边分别相等的两个三角形全等）
5. (教材习题第1题改编)如图，已知线段a，利用尺规作△ABC，使得AB＝ 2a，AC＝3a，BC＝4a(不写作法，保留作图痕迹)．
知识点3　三角形的稳定性
6. 下列生活实物中，没．有．运用三角形的稳定性的是 (　C　)
7. 如图，墙上置物架的底侧一般会各设计一根斜杆，与水平和竖直方向的 支架构成三角形，其中蕴含的数学道理是_______________.
8. 如图是由五根木条钉成的木架，要使该木架不变形，则至少需要钉上木 条的根数为(　B　)
9. 如图，已知∠AOB，用尺规作图如下：①以点O为圆心，任意长为半径 画弧，交OA于点M，交OB于点N；②以点N为圆心，MN为半径画弧，交 已画的弧于点C；③作射线OC；④连接MN，NC. 那么下列结论不．正．确．的 是(　D　)
10. 如图，在△ABC中，AB＝AC，AM＝AN，BN＝CM，若∠AMB＝ 126°，则∠MAN的度数为 ____．
第10题图
11. 如图，已知AB＝CD，BC＝DA，下列结论：①△ABC≌△CDA；② ∠BAC＝∠DCA；③AB∥CD；④∠BAD＋∠BCD＝180°，其中正确的 结论有 ___________(填序号)．
12. 如图，在△ABC中，∠ABC＝90°，点D，E分别为边AC，BC上一 点，连接BD，DE. 已知AB＝BE，AD＝DE.
(1)试说明：BD平分∠ABC；
(2) 若∠CDE＝20°，求∠A的度数．
解法二：因为∠BED＝180°－∠DEC，∠CDE＋∠C＝180°－∠DEC，所以∠BED＝∠CDE＋∠C，因为∠CDE＝20°，所以∠C＝∠BED－20°，因为△ABD≌△EBD，所以∠A＝∠BED，所以∠C＝∠A－20°，因为∠ABC＝90°，所以∠A＋∠C＝∠A＋∠A－20°＝90°，解得∠A＝55°.
13. (结论开放)如图，已知AB＝AC，AD＝AE，BD＝CE，B，D，E三点 共线，AC与BE相交于点F，请从结论①∠ADE＝∠CAE＋∠ACE；② ∠BAC＝∠BEC中任选一个进行说明．