数学九年级上册1.4 二次函数的应用一等奖课件ppt

这是一份数学九年级上册1.4 二次函数的应用一等奖课件ppt，共20页。PPT课件主要包含了齐声朗读，新知引入，t10t22，t10，t22，t²-2t0，tt-20，t2－t12s，新知讲解，一分钟背诵等内容，欢迎下载使用。
二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴的交点的横坐标x1，x2就是一元二次方程ax2＋bx＋c＝0(a≠0)的两个根。因此我们可以通过解方程ax2＋bx＋c＝0来求抛物线y＝ax2＋bx＋c与x轴交点的坐标；反过来，也可以由y＝ax2＋bx＋c的图象来求一元二次方程ax2＋bx＋c＝0的根。
从函数视角看，方程是什么？
从函数视角看，方程ax2＋bx＋c＝0(a≠0)是函数y＝ax2＋bx＋c(a≠0)的0点位置
函数值为0
0点位置
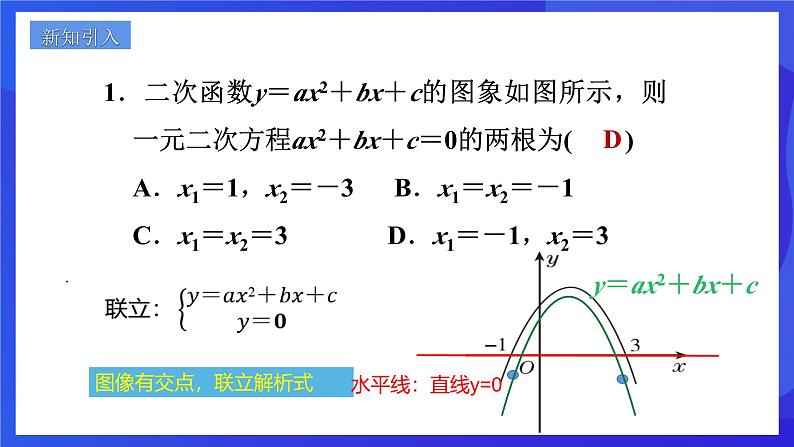
1．二次函数y＝ax2＋bx＋c的图象如图所示，则一元二次方程ax2＋bx＋c＝0的两根为(　　)A．x1＝1，x2＝－3 B．x1＝x2＝－1C．x1＝x2＝3 D．x1＝－1，x2＝3
图像有交点，联立解析式
解：h=10t-5t²
取h=0，－5t²+10t=0
球从弹起至回到地面需要时间:
取h=3.75，10t－5t²=3.75
，t1=0.5；t2=1.5
经过0.5s或1.5s球的高度达到3.75m。
就是球回到地面的时刻，
就是球从地面弹起的时刻，
从函数视角看，方程是函数的特殊位置
－5t²+10t-3.75=0
t²-2t+0.75=0
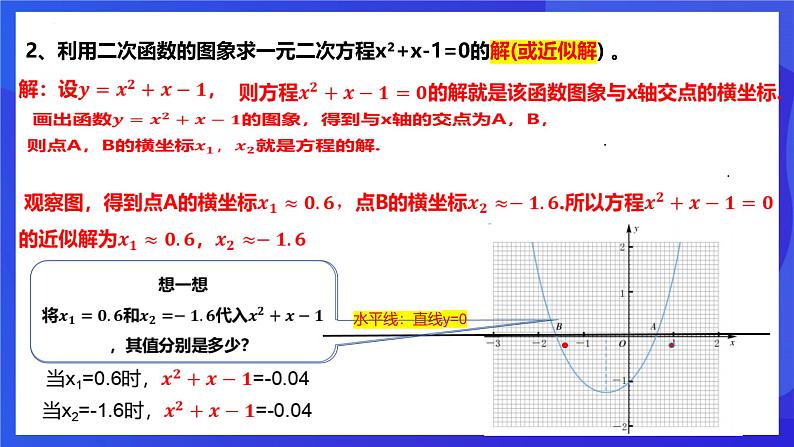
2、利用二次函数的图象求一元二次方程x²+x-1=0的解(或近似解) 。
解一元二次方程x²+x-1=0
a=1,b=1,c=-1
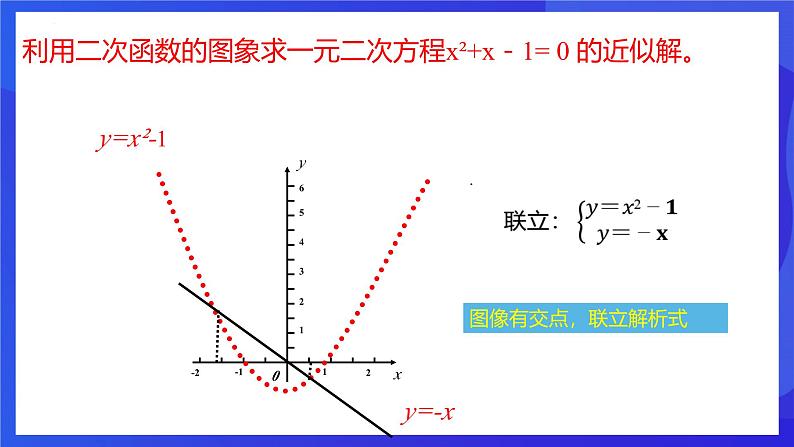
利用二次函数的图象求一元二次方程x²+x－1= 0 的近似解。
行到水穷处，坐看云起时
处绝境不要失望，因为那正是希望的开始
1．如图，是二次函数y＝ax2＋bx＋c的图象，图象上有两点分别为A(2.18，－0.61)，B(2.68，0.44)，则方程ax2＋bx＋c＝0的一个解只可能是(　　)A．2.18 B．2.68C．－0.51 D．2.55
自变量x 从 2.18增大到2.68，
函数值y 从 -0.61增大到0.44
2．根据下面表格的对应值，判断方程ax2＋bx＋c＝0(a≠0，a，b，c为常数)的一个解的范围是(　　)A. 3＜x＜3.23 B．3.23＜x＜3.24C． 3.24＜x＜3.25 D．3.25＜x＜3.26
函数值y 从 负变正--------
2.一元二次方程ax2+bx+c=m的根就是二次函数y=ax2+bx+c 与直线y=m（m是实数）图象交点的横坐标 .
2x2-2x-10=0,x2-x-5=0
4.62=(4.5+0.1)2
=20.25+0.9+0.01
知识点:　利用二次函数的图象求一元二次方程的近似根
(3)列表，在两个整数之间取值，并用计算器算出对应的y 值，当x 由x1变到x2，对应的y 值出现y1＞0，y2＜0(或y1＜0，y2＞0)且|y1|≠|y2|时，x1，x2中必有一个是方程的近似根，再比较|y1|和|y2|，若|y1|＜|y2|，则x1是方程的近似根；若|y1|＞|y2|，则x2是方程的近似根．
6、一球从地面抛出的运动路线呈抛物线， 如图，当球离抛出地的水平距离为 30m 时，达到最 大高度10m.⑴ 求球运动路线的函数解析式和自变量的取值范围；
⑶ 当球的高度为5m时,球离抛出地面的水平距离是多少m？
7.已知一个二次函数的图象与x轴的交点为（－2，0），（4 ，0 ）， 且顶点在函数y＝2x的图象上.求这个二次函数的表达式.
顶点的横坐标为x=1，则顶点的纵坐标为y=2.
把顶点坐标（1，2）代入上述表达式，得2=-9a，∴