初中数学浙教版九年级上册1.4 二次函数的应用完美版课件ppt

这是一份初中数学浙教版九年级上册1.4 二次函数的应用完美版课件ppt，文件包含浙教版9年级上册数学14二次函数的应用3课件pptx、浙教版9年级上册数学14二次函数的应用3教案doc、浙教版9年级上册数学14二次函数的应用3学案doc等3份课件配套教学资源，其中PPT共25页， 欢迎下载使用。

由b²-4ac的符号决定
b²-4ac﹥0，有两个交点
b²-4ac=0，只有一个交点
b²-4ac﹤0，没有交点
如何求二次函数图象的顶点坐标，与x轴的交点坐标，与y轴的交点坐标？
二次数函的图象与x轴有没有交点，由什么决定?
探究：求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标.
解：∵A、B在x轴上，∴它们的纵坐标为0， ∴令y=0，则x2-3x+2=0 解得：x1=1，x2=2； ∴A（1，0） ， B（2，0）
你发现方程 的解x1、x2与A、B的坐标有什么联系？
方程的解是函数图象与x轴的交点的横坐标.
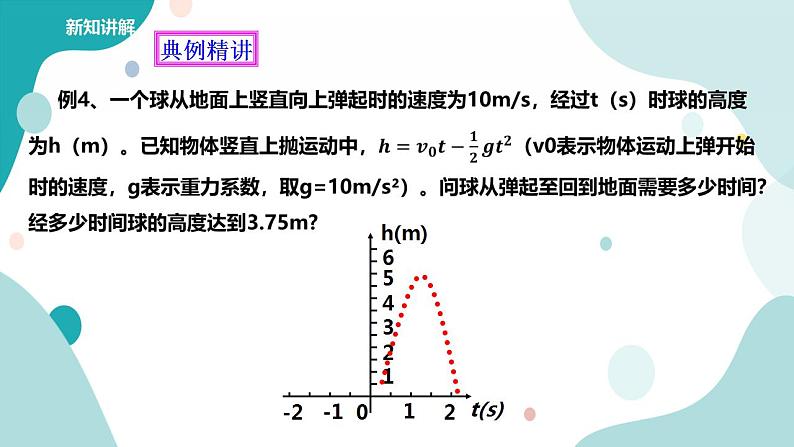
解：由题意，得h关于t的二次函数解析式为h=10t-5t²
取h=0，得一元二次方程10t－5t²=0
解方程得t1=0；t2=2
球从弹起至回到地面需要时间为t2－t1=2（s）
取h=3.75，得一元二次方程10t－5t²=3.75
解方程得t1=0.5；t2=1.5
答：球从弹起至回到地面需要时间为2（s）； 经过圆心的0.5s或1.5s球的高度达到3.75m。
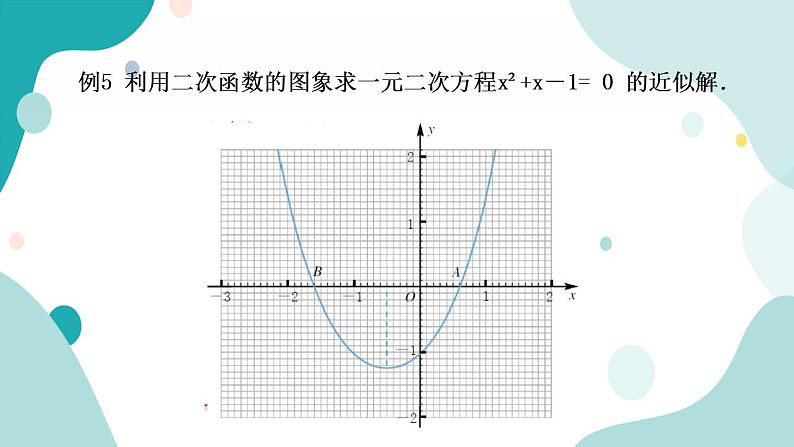
例5 利用二次函数的图象求一元二次方程x²+x－1= 0 的近似解．
在例5中，我们把一元二次方程 x²+x-1= 0 的解看做是抛物线 y=x²+x-1 与x轴交点的横坐标，利用图象求出了方程的近似解．如果把方程x²+x-1 = 0变形成 x² = -x+1，那么方程的解也可以看成怎样的两个函数的交点的横坐标？用不同图象解法试一试，结果相同吗？在不使用计算机画图象的情况下，你认为哪一种方法较为方便？
利用二次函数的图象求一元二次方程 x²+x-1= 0 的近似解．
反过来，也可利用二次函数的图象求一元二次方程的解.
二次函数y=ax²+bx+c
一元二次方程ax²+bx+c=0
两根为x1=m；x2=n
函数与x轴交点坐标为：（m，0）；（n，0）
1．在平面直角坐标系中，抛物线y＝x2－1与x轴的交点的 个数是(　 　) A．3　　　　　　　 B．2 C．1 D．0
2．根据下表的对应值：
判断方程ax2＋bx＋c＝0(a≠0，b，c为常数)一个解x的范围是 (　 　)
A．3　3.利用函数图象判断方程2x2－x－1＝0有没有实数解，若有，求出它的解(精确到十分位)．【解析】 用函数图象解方程有两种方法：一是求函数y＝2x2－x－1与x轴交点的横坐标；二是求函数y＝2x2与y＝x＋1的图象的交点的横坐标．
解：方法一：设y＝2x2－x－1，则方程2x2－x－1＝0的解就是该函数图象与x轴交点的横坐标．在平面直角坐标系内画出函数y＝2x2－x－1的图象如图(1)所示，得到与x轴交点为A，B，则A，B的横坐标x1，x2就是方程的解．由图象可知方程2x2－x－1＝0的解为x1＝－0.5，x2＝1.0.
方法二：设y＝2x2与y＝x＋1，则方程2x2－x－1＝0的解就是函数y＝2x2与y＝x＋1的图象交点的横坐标．在同一平面直角坐标系中画出函数y＝2x2与y＝x＋1的图象，如图(2)所示，得到两函数图象有两个交点A，B，即方程2x2－x－1＝0有两个实数解，且A，B两点的横坐标x1，x2就是方程的解．由图象可得方程2x2－x－1＝0的解为x1＝－0.5，x2＝1.0.
【点悟】 用函数图象解方程有两种方法：(1)求二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴的交点的横坐标；(2)求二次函数y＝ax2与一次函数y＝－bx－c的图象的交点的横坐标．
4.二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，根据图象解答下列问题：(1)求方程ax2＋bx＋c＝0的两个根．(2)求不等式ax2＋bx＋c>0的解集．(3)求y随x的增大而减小的自变量x的取值范围．(4)若方程ax2＋bx＋c＝k有两个不相等的实数根，求k的取值范围．
【解析】(1)方程ax2＋bx＋c＝0的两个根，即抛物线y＝ax2＋bx＋c(a≠0)与x轴交点的横坐标．(2)不等式ax2＋bx＋c>0的解集即为抛物线y＝ax2＋bx＋c>0所对应的x的值．(3)抛物线的对称轴是直线x＝2.当x>2时，y随x的增大而减小．(4)方程ax2＋bx＋c＝k的根，可以看作抛物线y＝ax2＋bx＋c与直线y＝k的交点情况．因为抛物线的最大值为y＝2，所以方程ax2＋bx＋c＝k有两个不相等的实数根对应的是抛物线y＝ax2＋bx＋c与直线y＝k有两个交点．故k<2.
解：(1)x1＝1，x2＝3；(2)12； (4)k<2.
【点悟】(1)当抛物线y＝ax2＋bx＋c(a≠0)与x轴相交时，交点的横坐标就是一元二次方程ax2＋bx＋c＝0的根．(2)不等式ax2＋bx＋c>0(或ax2＋bx＋c<0)的解集就是抛物线y＝ax2＋bx＋c(a≠0)>0(或y＝ax2＋bx＋c(a≠0)<0)所对应的x的取值范围．(3)方程ax2＋bx＋c＝k的解可以看作求抛物线y＝ax2＋bx＋c与直线y＝k的交点的横坐标．这样，我们就可以把方程、函数、不等式这三大块代数知识有机地联系起来了．
1．用一元二次方程求二次函数的图象与x轴(或平行于x轴的直线)的交点坐标二次函数图象与x轴交点坐标：二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴的交点的横坐标x1，x2就是一元二次方程ax2＋bx＋c＝0(a≠0)的两个根．因此可以用方程ax2＋bx＋c＝0(a≠0)来求抛物线y＝ax2＋bx＋c(a≠0)与x轴的交点坐标．二次函数图象与平行于x轴的直线的交点坐标：二次函数y＝ax2＋bx＋c(a≠0)与平行于x轴的直线y＝n的交点横坐标就是一元二次方程ax2＋bx＋c＝n(a≠0)的两个根．
2．利用二次函数的图象求一元二次方程的解或近似解步骤：(1)画出二次函数y＝ax2＋bx＋c(a≠0)的图象．(2)确定一元二次方程ax2＋bx＋c＝0(a≠0)的根的取值范围，即确定抛物线y＝ax2＋bx＋c(a≠0)与x轴的交点的横坐标的大致范围．(3)在(2)确定的范围内，用计算器进行探索，即在(2)范围内，从大到小或从小到大依次取值，用表格的形式求出相应的y值．(4)确定一元二次方程ax2＋bx＋c＝0(a≠0)的解(或近似解)．在(3)中最接近0的y值所对应的x值即是一元二次方程ax2＋bx＋c＝0(a≠0)的解或近似解．