数学八年级下册18.2.1 矩形完整版课件ppt

这是一份数学八年级下册18.2.1 矩形完整版课件ppt，文件包含人教版数学八年级下册18211《矩形的性质》同步课件pptx、人教版数学八年级下册18211《矩形的性质》分层练习原卷版docx、人教版数学八年级下册18211《矩形的性质》分层练习解析版docx等3份课件配套教学资源，其中PPT共30页， 欢迎下载使用。
观察生活中的生活中的矩形，你还能举出哪些例子？
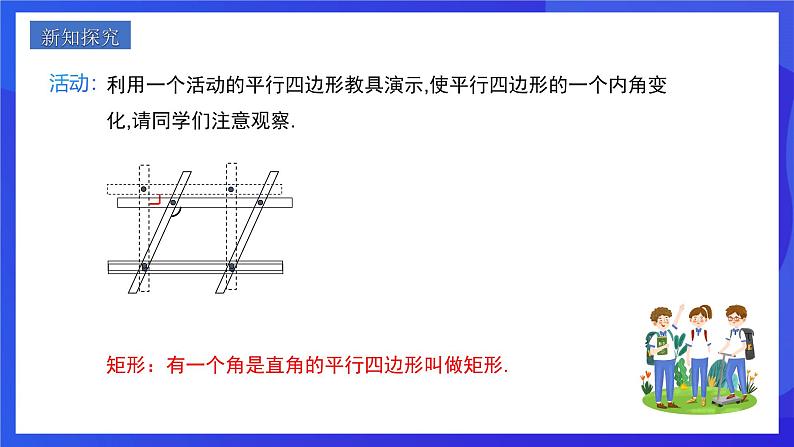
利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请同学们注意观察.
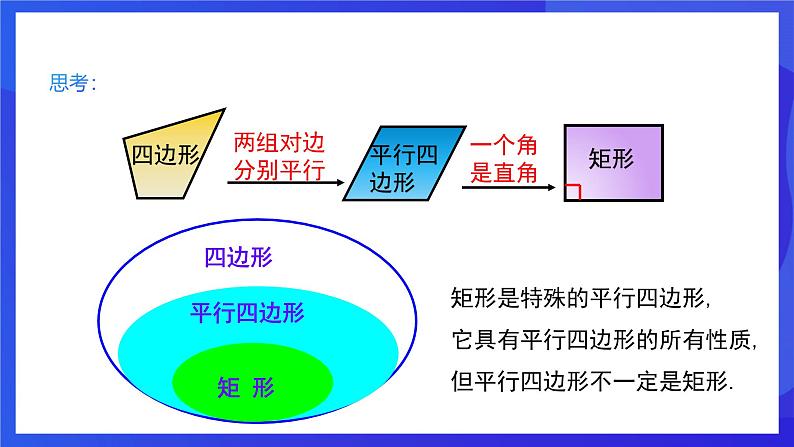
矩形：有一个角是直角的平行四边形叫做矩形.
矩形是特殊的平行四边形, 它具有平行四边形的所有性质, 但平行四边形不一定是矩形.
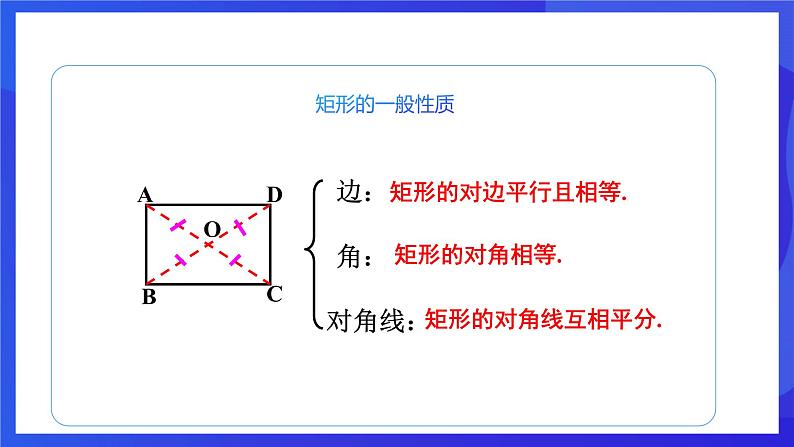
矩形的对边平行且相等.
矩形的对角线互相平分.
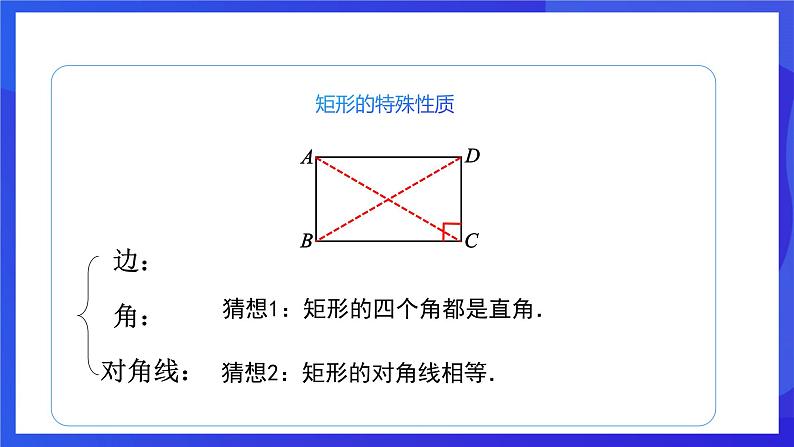
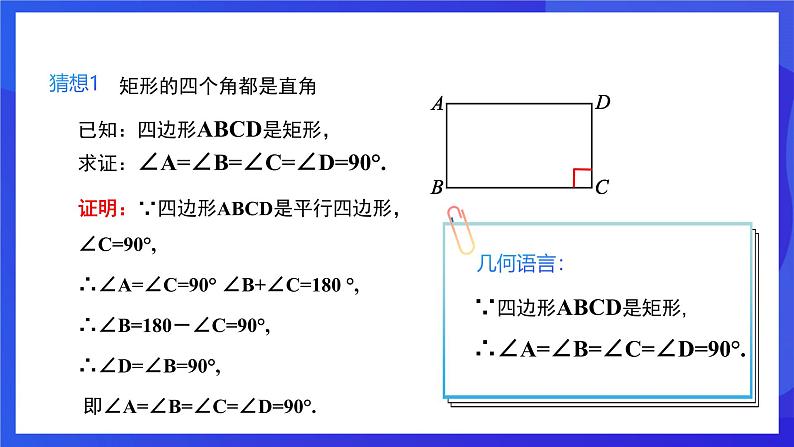
猜想1：矩形的四个角都是直角．
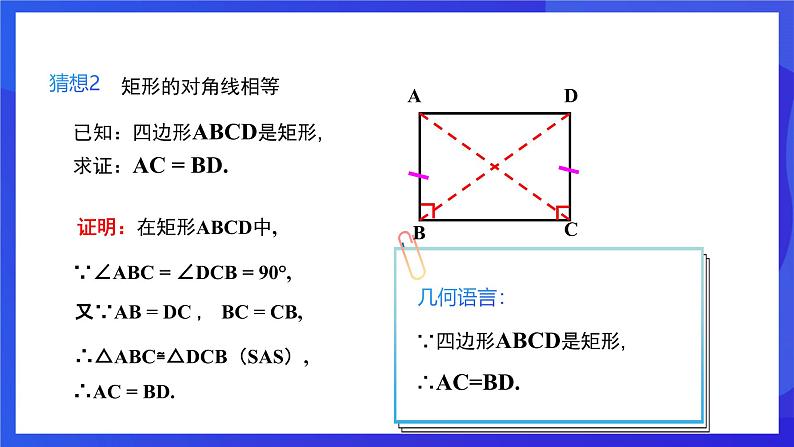
猜想2：矩形的对角线相等．
证明：∵四边形ABCD是平行四边形， ∠C=90°,∴∠A=∠C=90° ∠B+∠C=180 °,∴∠B=180－∠C=90°,∴∠D=∠B=90°, 即∠A=∠B=∠C=∠D=90°.
∵四边形ABCD是矩形,∴∠A=∠B=∠C=∠D=90°.
证明：在矩形ABCD中,
∵∠ABC = ∠DCB = 90°,
又∵AB = DC ， BC = CB,
∴△ABC≌△DCB（SAS）,
∵四边形ABCD是矩形,∴AC=BD.
矩形是轴对称图形，也是中心对称图形.
∠DAB=∠ABC=∠BCD=∠CDA=90° ∠AOB=∠DOC ∠AOD=∠BOC∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
△OAB △ OBC △OCD △OAD
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB△OAB≌△OCD △OAD≌△OCB
如图，矩形 ABCD 的两条对角线 AC ，BD 相交于点 O，AC = 4 cm， ∠AOB = 60°. 求 BC 的长.
∴ △AOB 是等边三角形.
∴ AB = OA = 2 cm.
又∠AOB = 60°，
∵ ∠ABC = 90°，
解 ∵ 四边形 ABCD 是矩形，
∴ 在 Rt△ABC 中，
如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.求证：DF=DC.
证明：连接DE.∵AD =AE,∴∠AED =∠ADE.∵四边形ABCD是矩形,∴AD∥BC,∠C=90°.∴∠ADE=∠DEC, ∴∠DEC=∠AED.又∵DF⊥AE, ∴∠DFE=∠C=90°.
又∵DE= DE,∴△DFE ≌△DCE,∴DF=DC.
如图，在矩形 ABCD 中， E 是 AB 上一点，F 是 AD 上一点，EF⊥FC，且 EF = FC，DF = 4 cm，求 AE 的长.
解: ∵ EF ⊥ FC，∴ ∠AFE+∠DFC=90°.又∠DCF+∠DFC=90°，∴ ∠DCF = ∠AFE ．又∠A=∠D=90°，EF=FC，∴Rt△FAE ≌ Rt△CDF．∴AE = DF = 4 cm.
如图，在矩形 ABCD 中，AB ＝ 3 cm， AD ＝ 4 cm，过对角线 BD 的中点 O 作 BD 的垂线 EF，分别交 AD，BC于点 E，F， 求 AE 的长.
解：连接 BE，易得Rt△EOB≌Rt△EOD，∴BE=DE.在Rt△AEB中，AB2+AE2=BE2=DE2，∴32+AE2=(4-AE)2，∴9+AE2=16-8AE+AE2，∴AE = cm.
如图：矩形ABCD的对角线AC与BD交于点O，那么BO是Rt△ABC中一条怎样的特殊线段？它与AC有什么大小关系呢？由此你能得到怎样的结论呢？
提示：大家可以通过测量初步猜测
直角三角形斜边上的中线等于斜边的一半.
证明: 延长BO至D, 使OD=BO, 连接AD、DC.
∵AO=OC, BO=OD，∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴平行四边形ABCD是矩形，
∵△ABC为直角三角形，BO为AC的中线,
如图，已知BD，CE是△ABC不同边上的高，点G，F分别是BC，DE的中点，试说明GF⊥DE.
解：连接EG，DG.∵BD，CE是△ABC的高，∴∠BDC＝∠BEC＝90°.∵点G是BC的中点，∴EG＝2(1)BC，DG＝2(1)BC.∴EG＝DG.又∵点F是DE的中点，∴GF⊥DE.
如图，在△ABC中，AD是高，E、F分别是AB、AC的中点．(1)若AB＝10，AC＝8，求四边形AEDF的周长；
解：（1）∵AD是△ABC的高， E、F分别是AB、AC的中点，∴DE＝AE＝ AB＝ ×10＝5， DF＝AF＝ AC＝ ×8＝4，∴四边形AEDF的周长＝ AE＋DE＋DF＋AF＝ 5＋5＋4＋4＝18 .
(2)求证：EF垂直平分AD.
（2）证明：∵DE＝AE，DF＝AF，∴E、F在线段AD的垂直平分线上， ∴EF垂直平分AD.
1.矩形是轴对称图形和中心对称图形
2.矩形四个角都是直角
3.矩形的对角线相等且相互平分
直角三角形斜边上的中线等于斜边的一半
4.具有平行四边形的一切性质
1.下列说法错误的是（ ）A. 矩形的对角线互相平分。 B. 矩形的对角线相等。C. 有一个角是直角的四边形是矩形。 D. 有一个角是直角的平行四边形叫做矩形。
2. 用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是( )A. 48 cm,12 cm B. 48 cm,16 cm; C. 44 cm,16 cm D. 45 cm,15 cm.
3. 填空：（1）矩形的定义中有两个条件：一是__________ ，二是_______________ .（2）已知矩形的一条对角线与一边的夹角为30°，则矩形两条对角线相交所得的四个角的度数分别为________、________ 、 ______ 、 _______ 。
（3）已知矩形的一条对角线长为10 cm，两条对角线的一个交角为120°，则矩形的边长分别为______ cm，______ cm， ______ cm，_______ cm.
4.如图，在矩形ABCD中，AD＝3AB，点G，H分别在AD，BC上，连接BG，DH，且BG∥DH，当等于多少时，四边形BHDG为菱形 ( 　　)A．　　　B．　　　C．　　　D．
5.如图，矩形ABCD沿着对角线BD折叠，使点C落在C′处，BC′交AD于点E，AD＝8，AB＝4，则DE的长为______.
6.如图，EF过矩形ABCD对角线的交点O，且分别交AB、CD于E、F，那么阴影部分的面积是矩形ABCD面积的_________.
　　　　　　　　　　　　　
6.一个矩形的两条对角线的一个夹角为60∘，对角线长15，求这个矩形较短边的长.
7.如图，在矩形ABCD中，两条对角线AC与BD相交于点O，AB=6，OA=4.求BD与AD的长.
解：∵OA＝4，∴BD＝AC＝2OA＝8，AD＝BC＝ ＝ ＝2 .
8.已知：如图，矩形ABCD中，AB长8cm，对角线比AD长4cm.求AD的长及点A到BD的距离AE的长．
解：设AD＝x cm，则对角线长(x＋4)cm， 在Rt△ABD中，由勾股定理：x2＋82＝(x＋4)2， 解得x＝6，则AD＝6 cm； 利用面积公式，可得到两直角边、 斜边及斜边上的高有一个基本关 系式：AE·DB＝AD·AB， 解得AE＝4.8 cm.