初中数学18.1 平行四边形精品课件ppt

这是一份初中数学18.1 平行四边形精品课件ppt，文件包含人教版数学八年级下册18123《三角形的中位线》同步课件pptx、人教版数学八年级下册18123《三角形的中位线》分层练习原卷版docx、人教版数学八年级下册18123《三角形的中位线》分层练习解析版docx等3份课件配套教学资源，其中PPT共28页， 欢迎下载使用。
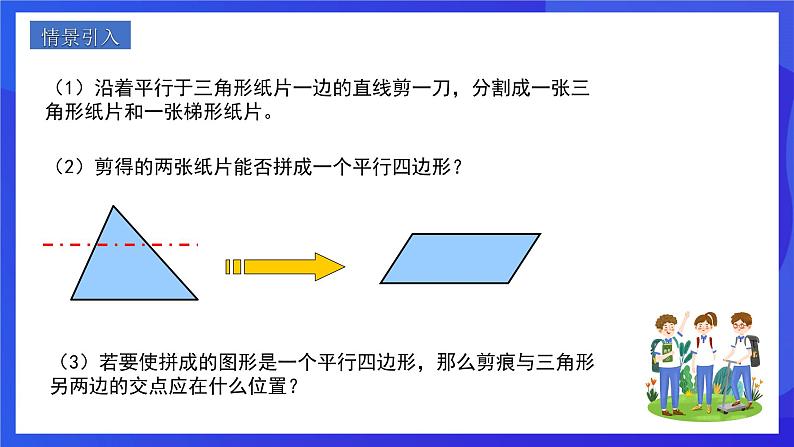
（1）沿着平行于三角形纸片一边的直线剪一刀，分割成一张三角形纸片和一张梯形纸片。
（2）剪得的两张纸片能否拼成一个平行四边形？
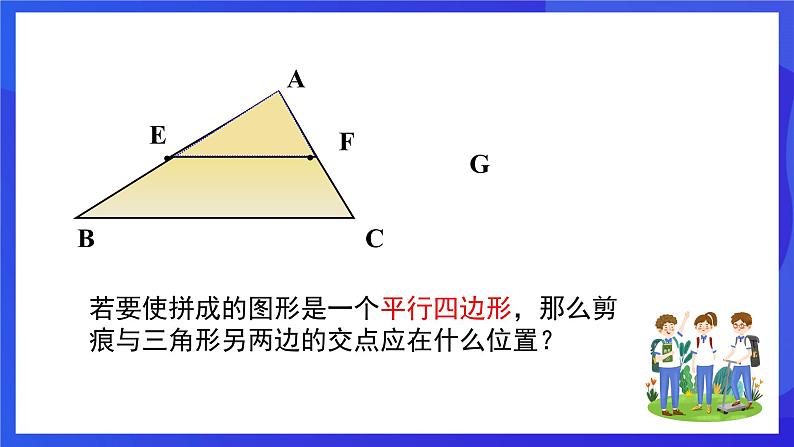
（3）若要使拼成的图形是一个平行四边形，那么剪痕与三角形另两边的交点应在什么位置？
若要使拼成的图形是一个平行四边形，那么剪痕与三角形另两边的交点应在什么位置？
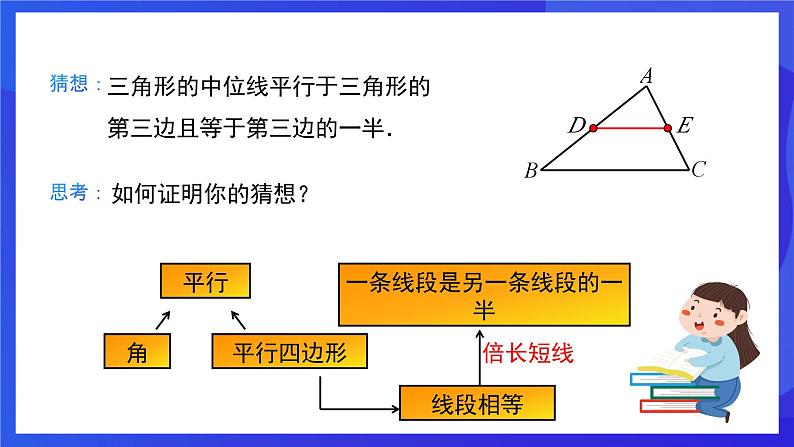
定义：连接三角形两边中点的线段叫做三角形的中位线.
如图，在△ABC中，D、E分别是AB、AC的中点，连接DE，则线段DE就称为△ABC的中位线.
如图，DE是△ABC的中位线，DE与BC有怎样的关系？
度量一下你手中的三角形，看看是否有同样的结论？并用文字表述这一结论．
一条线段是另一条线段的一半
三角形的中位线平行于三角形的第三边且等于第三边的一半．
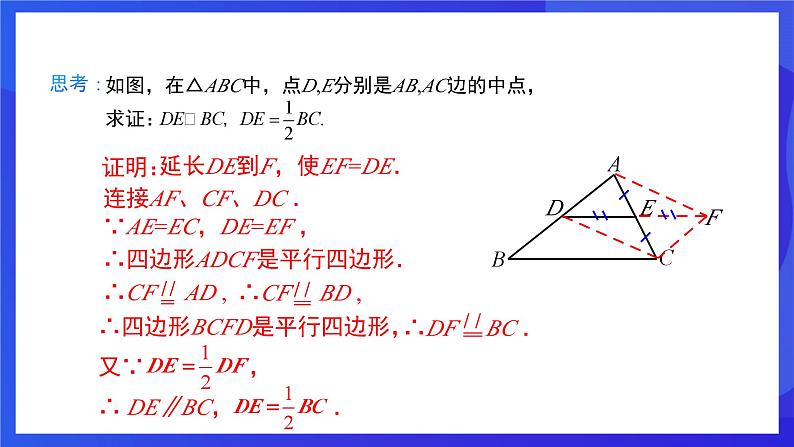
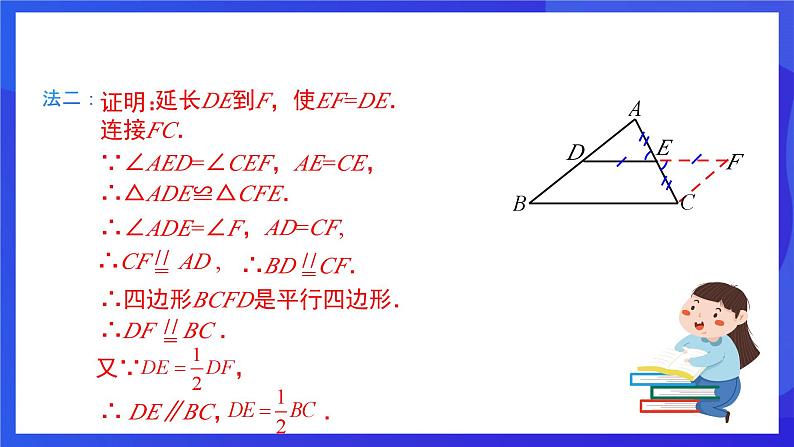
延长DE到F，使EF=DE．
连接AF、CF、DC ．
∵AE=EC，DE=EF ，
∴四边形ADCF是平行四边形．
∴四边形BCFD是平行四边形，
∴ DE∥BC， ．
如图，在△ABC中，点D,E分别是AB,AC边的中点，求证：
∴四边形BCFD是平行四边形．
∴△ADE≌△CFE．
∵∠AED=∠CEF，AE=CE，
∴ DE∥BC， ．
①中位线DE、EF、DF把△ABC分成四个全等的三角形；有三组共边的平行四边形，它们是四边形ADFE和BDEF，四边形BFED和CFDE，四边形ADFE和DFCE.
②顶点是中点的三角形，我们称之为中点三角形；中点三角形的周长是原三角形的周长的一半.面积等于原三角形面积的四分之一.
画出三角形的所有中线和中位线，并说出中位线和中线的区别.
如图，已知△ABC，D、E、F分别是BC、AB、AC边上的中点.
（1）若∠AEF=60°，则∠B= 度
（2）若BC=8cm，则EF= cm
（4）若△ABC的面积为S，则△DEF的面积_____；
（3）若△ABC的周长为18cm，则△DEF的周长是______；图中有_____个平行四边形；
如图, MN 为△ABC 的中位线,若∠ABC =59° 则∠AMN = ,若MN =13 ,则BC =_______.
如图,已知△ABC中,AB = 4㎝,BC=4.6 ㎝ AC=6㎝ 且D,E,F分别为 AB,BC,AC边的中点,则△DEF的周长是 ㎝.
4.在△ABC中，E、F、G、H分别为AC、CD、 BD、 AB的中点，若AD=3，BC=8，则四边形EFGH的周长是 .
(1) 若AC=BD，四边形EFGH是什么图形？
如图，顺次联结四边形ABCD四边的中点E、F、G、H，
(2) 若AC⊥BD，四边形EFGH是什么图形？
(3) 若AC=BD且 AC⊥BD，四边形EFGH是什么图形？
(1) 若AC=BD，四边形EFGH是菱形
(2) 若AC⊥BD，四边形EFGH是矩形
(3) 若AC=BD且 AC⊥BD，四边形EFGH是正方形
如右图，A、B两点被池塘隔开，现在要测量出A、B两点间的距离 ，但又无法直接去测量，怎么办？
这时，在A、B外选一点C，连结AC和BC，并分别找出AC和BC的中点D、E，如果能测量出DE的长度，也就能知道AB的距离了.这是什么道理呢？
证明：∵D、E分别为AB、AC的中点，∴DE为△ABC的中位线，∴DE∥ BC，DE= BC.∵CF= BC，∴DE=FC．
解：∵DE∥FC，DE=FC，∴四边形DEFC是平行四边形，∴DC=EF，∵D为AB的中点，等边△ABC的边长是2，∴AD=BD=1，CD⊥AB，BC=2，∴EF=DC= ．
如图，E为▱ABCD中DC边的延长线上一点，且CE＝DC，连接AE，分别交BC、BD于点F、G，连接AC交BD于O，连接OF，判断AB与OF的位置关系和大小关系，并证明你的结论．
解：AB∥OF，AB＝2OF.证明如下：∵四边形ABCD是平行四边形， ∴AB＝CD，AB∥CD，OA＝OC，∴∠BAF＝∠CEF，∠ABF＝∠ECF.∵CE＝DC，∴AB＝CE,∴△ABF≌△ECF(ASA)，∴BF＝CF.∵OA＝OC，∴OF是△ABC的中位线，∴AB∥OF，AB＝2OF.
如图，在△ABC中，AB=6cm，AC=10cm，AD平分∠BAC，BD⊥AD于点D，BD的延长线交AC于 点F，E为BC的中点，求DE的长．
解：∵AD平分∠BAC，BD⊥AD，∴AB=AF=6cm，BD=DF，∴CF=AC-AF=4cm，∵BD=DF，E为BC的中点，∴DE= CF=2cm．
三角形中位线平行于第三边，并且等于它的一半
三角形的中位线定理的应用
1.如图，在△ABC中，AB=6，AC=10，点D，E，F分别是AB，BC，AC的中点，则四边形ADEF的周长为（　　） A.8 B.10 C.12 D.16
2.如图，在▱ABCD中，AD=8，点E，F分别是BD，CD的中点，则EF等于 （　　）A.2 B.3 C.4 D.5
3. 如图，△ABC中，D、E分别是AB、AC中点．
（1） 若DE=5，则BC= ．
（2） 若∠B=65°，则∠ADE= °．
（3） 若DE+BC=12，则BC= ．
4.如图，A，B两点被池塘隔开，在A，B外选一点C，连接AC和BC，并分别找出AC和BC的中点M，N，如果测得MN=20m，那么A，B两点间的距离为______m．
5.如图，在△ABC中，D、E分别为AC、BC的中点，AF平分∠CAB，交DE于点F.若DF＝7，求AC的长
解：∵D、E分别为AC、BC的中点，∴DE∥AB，∴∠2＝∠3.又∵AF平分∠CAB，∴∠1＝∠3，∴∠1＝∠2，∴AD＝DF＝7，∴AC＝2AD＝2DF＝14.
6.如图，在四边形ABCD中，AB=CD，M、N、P分别是AD、BC、BD的中点，∠ABD=25°，∠BDC=75°，求∠PMN的度数．
解：∵M、N、P分别是AD、BC、BD的中点，∴PN，PM分别是△CDB与△DAB的中位线，∴PM= AB，PN= DC，PM∥AB，PN∥DC，∵AB= CD，∴PM=PN，∴△PMN是等腰三角形，∵PM∥AB，PN∥DC，∴∠MPD=∠ABD=25°，∠BPN=∠BDC=75°，∴∠MPN=∠MPD+(180°−∠NPB)=130°，∴∠PMN=(180°−130°)÷ 2 =25°．