初中数学人教版八年级下册18.2.1 矩形背景图课件ppt

这是一份初中数学人教版八年级下册18.2.1 矩形背景图课件ppt，共24页。PPT课件主要包含了教学目标，新课导入，新知探究，知识归纳，∴∠A90°，课堂小结，矩形的性质，课堂小测，B对边相等，A对角相等等内容，欢迎下载使用。
1.矩形性质定理的运用 ;（重点）2.利用矩形的性质定理进行证明和计算 .（难点）
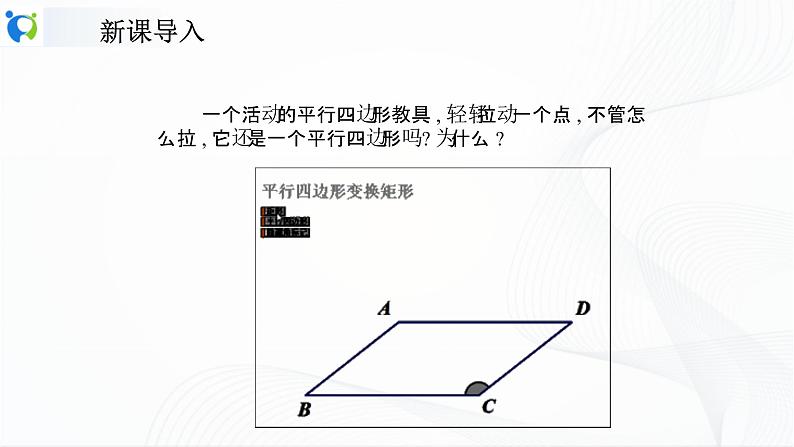
　 一个活动的平行四边形教具 , 轻轻拉动一个点 , 不管怎么拉 , 它还是一个平行四边形吗 ? 为什么 ?
下面我们先来看一些图片 , 考虑什么样的图形是矩形 .
请同学们观察上面的图片 , 思考下面的问题 :(1)这些图形有哪些共同特点 ?(2)什么样的图形是矩形 ? 你能给矩形下个定义吗 ?
有一个角是直角的平行四边形叫做矩形 .
矩形是特殊的平行四边形
猜想：猜想1: 矩形的四个角都是直角 ;　 猜想2: 矩形的对角线相等 .　 追问 : 你能证明这些猜想吗 ?
矩形是一个特殊的平行四边形 , 除了具有平行四边形的所有性质外 , 还有哪些特殊性质呢 ?
求证 : 矩形的四个角都是直角 .
已知 : 如图 , 四边形ABCD是矩形 ,
求证 : ∠A=∠B=∠C=∠D=90°.
证明 : ∵四边形ABCD是矩形 ,
又∵矩形ABCD是平行四边形,
∴ ∠A=∠C , ∠B = ∠D , ∠A +∠B = 180° ,
∴ ∠A=∠B=∠C=∠D=90° .即矩形的四个角都是直角 .
已知 : 如图 , 四边形ABCD是矩形 , 求证 : AC = BD .
证明 : ∵ 四边形ABCD是矩形 ,
∴ ∠ABC = ∠DCB = 90° ,
AB = DC , ∠ABC = ∠DCB , BC = CB ,
∴ △ABC ≌△DCB ,
∴ AC = BD .
求证 : 矩形的对角线相等 .
在△ABC和△DCB中 ,
即矩形的对角线相等 .
矩形性质1 : 矩形的四个角都是直角 .
用符号语言表述为 :∵ 四边形ABCD是矩形 ,∴ ∠A=∠B=∠C=∠D=90° .
矩形性质2 : 矩形的对角线相等 .
用符号语言表述为 :∵ AC和BD是矩形ABCD的对角线 ,∴ AC=BD .
如图 , 在矩形ABCD中 , AC , BD相交于点O .根据矩形的性质 ,AO= = = = AC= .
直角三角形斜边上的中线等于斜边的一半 .
用符号语言表述为 :在Rt△ABC中 , BO是斜边AC上的中线 ,∴BO= AC .　
(1)直角三角形中 , 斜边上的中线把直角三角形 分成两个等腰三角形 , 这两个等腰三角形的 面积相等 .
(2)在直角三角形中 , 如果遇到斜边的中点 , 可以 考虑利用这一性质 .
(3)直角三角形斜边上的中线的性质一般可以 用来证明线段相等或线段的倍分问题 .
例1：如图 , 矩形ABCD的对角线AC , BD相交于点O , ∠AOB=60° , AB=4 . 求矩形对角线的长 .
解 : ∵四边形ABCD是矩形 ,　 ∴ AC与BD相等且互相平分,　 ∴ OA=OB .　 又∠AOB=60° ,　 ∴ △AOB是等边三角形 .　 ∴ OA=AB=4 .　 ∴ AC=BD=2OA=8 .
例2：如图 , 在矩形ABCD中 , 对角线AC , BD相交于点O , 点E , F分别 在边AD , BC上 , 且DE=CF , 连接OE , OF . 求证OE=OF .
证明:∵ 四边形ABCD为矩形 , ∴ ∠ADC=∠BCD=90°, AC=BD , OD= BD , OC= AC . ∴ OD=OC . ∴ ∠ODC=∠OCD . ∴ ∠ADC-∠ODC=∠BCD-∠OCD , 即∠EDO=∠FCO . 又∵ DE=CF , ∴△ODE ≌△OCF . ∴ OE=OF .
有一个角是直角的平行四边形叫做矩形
矩形性质1 : 矩形的四个角都是直角
矩形性质2 : 矩形的对角线相等
直角三角形斜边上的中线等于斜边的一半
1.矩形具有而一般平行四边形不具有的性质是 ( )
D.对角线互相平分
2.如图,一个矩形纸片,剪去部分后得到一个三角形,则图中 ∠1+∠2的度数是　 (　　)　A.30°　　 B.60° C.90°　 D.120°
3.如图 , 把矩形纸片沿对角线BD折叠 , 重叠部分为△EBD , 则下列 说法错误的是　 　(　　) A. AB=CD B. ∠BAE=∠DCE 　 C. EB=ED D. ∠ABE一定等于30°
4.如图 , O是矩形ABCD的对角线AC的中点 , M是AD的中点 , 若AB=5 , AD=12 , 则四边形ABOM的周长为　　. 
5.矩形ABCD的周长为 40cm , O是它的对角线交点 , 若△AOB的周长比 △AOD的周长多 4cm , 则矩形ABCD的最长边的长为　　　　. 
6.如图 , 用8块相同的长方形地砖拼成一个矩形地面 , 则每块长方形 地砖的长和宽分别是 .
45cm , 15cm
7.如图 , 已知矩形ABCD , 点E为矩形外一点 , 且AE=DE . 求证BE=CE .
证明 : ∵AE=DE , ∴∠EAD=∠EDA , 由四边形ABCD是矩形得 , AB=CD , ∠BAD=∠CDA=90° , ∴∠EAD+∠BAD=∠EDA+∠CDA , 即∠BAE=∠CDE , 在△ABE和△DCE中 , ∴△ABE ≌△DCE , ∴BE=CE .
8.如图 , 矩形 ABCD中 , AB长 8cm , 对角线比AD边长 4cm . 求AD的长及点A到BD的距离(即AE的长) .
解 : 设AD为 x cm , 则对角线BD的长为 (x+4)cm . 在Rt△ABD中 , 由勾股定理得x2+82=(x+4)2 , 解得x=6, 则AD=6cm . 由三角形的面积公式得AE·DB=AD·AB , 代入解得 AE=4.8cm .