数学八年级下册17.1 勾股定理完美版课件ppt

这是一份数学八年级下册17.1 勾股定理完美版课件ppt，文件包含人教版数学八年级下册1711《勾股定理》同步课件pptx、人教版数学八年级下册1711《勾股定理》分层练习原卷版docx、人教版数学八年级下册1711《勾股定理》分层练习解析版docx等3份课件配套教学资源，其中PPT共27页， 欢迎下载使用。
相传2500年前，一次，毕达哥拉斯去朋友家作客．在宴席上他看着朋友家的方砖地面发起呆来．主人觉得非常奇怪，就想过去问他．谁知毕达哥拉斯突然恍然大悟的样子，站起来，大笑着跑回家去了.后来知道是因为他从中发现了直角三角形三边的数量关系，赶着回家证明去了． 那么，他朋友家的地板到底是怎样呢？我们也观察一下看看能发现什么？
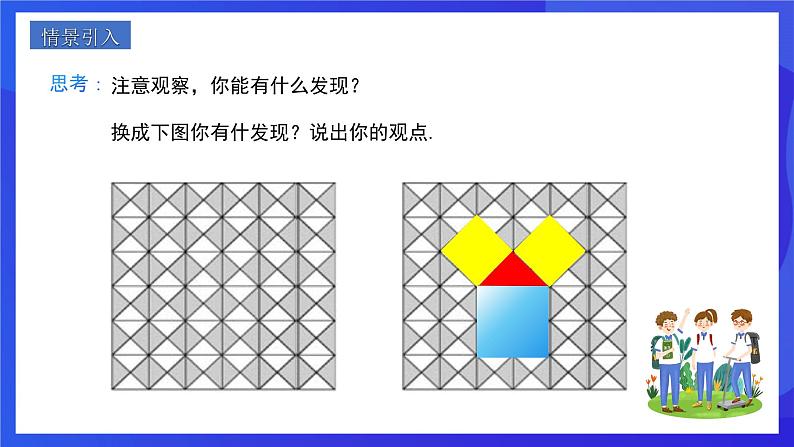
注意观察，你能有什么发现？
换成下图你有什发现？说出你的观点.
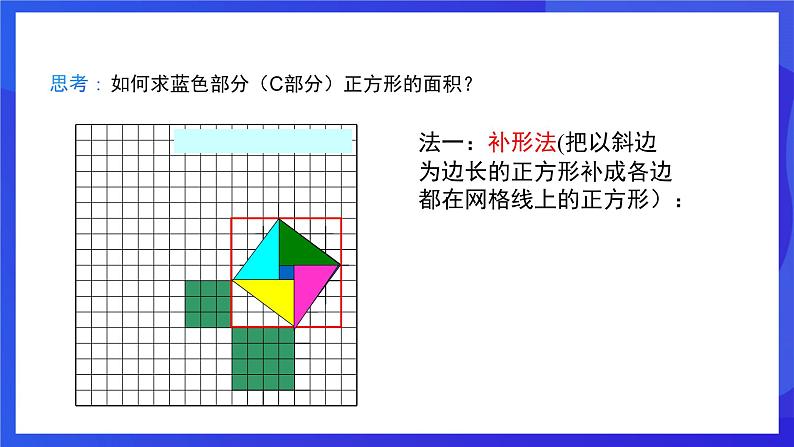
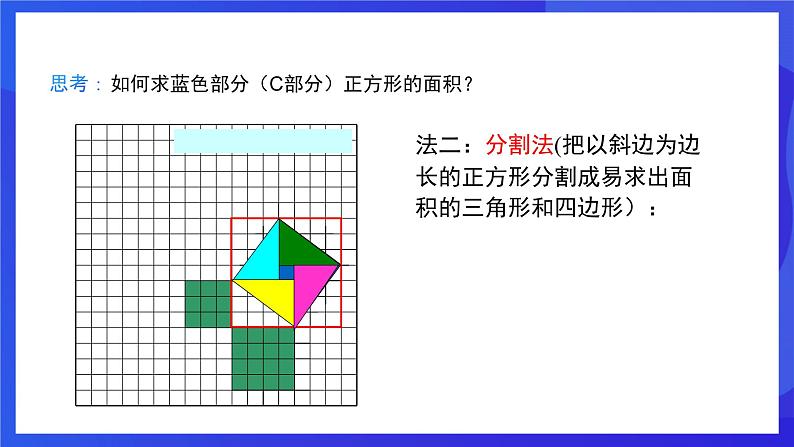
如何求蓝色部分（C部分）正方形的面积？
每个小方格的面积均为1
法一：补形法(把以斜边为边长的正方形补成各边都在网格线上的正方形）：
法二：分割法(把以斜边为边长的正方形分割成易求出面积的三角形和四边形）：
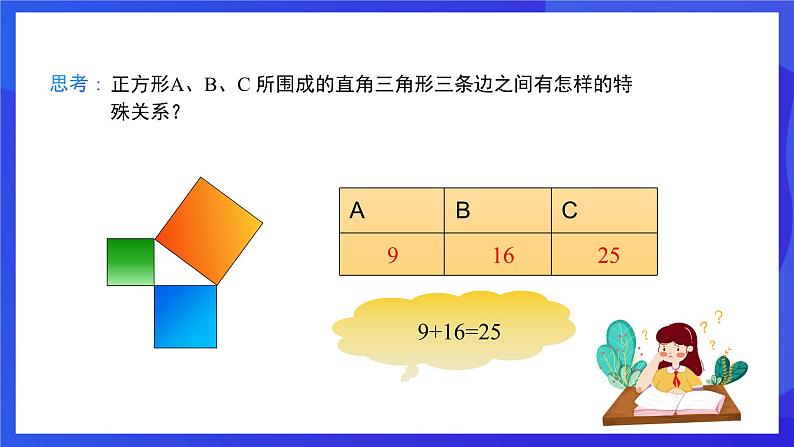
正方形A、B、C 所围成的直角三角形三条边之间有怎样的特殊关系？
三个正方形面积之间的关系能用直角三角形 的边来表示吗？
通过上面的研究，你能发现直角三角形三边的长之间有怎样的关系吗？
准备四个全等的直角三角形（设两条直角边分别为a，b， 斜边c）；
你能用这四个直角三角形拼成一个正方形吗？
你拼的正方形中是否含有以斜边c为边 的正方形？
你能否就你拼出的图说明a2+b2=c2？
大正方形的面积可以表示为 ；也可以表示为 .
S小正方形＝(b-a)2,
∴S大正方形＝4·S三角形＋S小正方形，
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智，它是我国古代数学的骄傲.因此，这个图案被选为2002年在北京召开的国际数学家大会的会徽.
∴a2+b2+2ab=c2+2ab，
∴a2 +b2 =c2.
∵S大正方形=(a+b)2=a2+b2+2ab,
∴a2 + b2 = c2.
美国第二十任总统伽菲尔德的“总统证法”.
在我国又称商高定理，在外国则叫毕达哥拉斯定理，或百牛定理.
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
在中国古代，人们把弯曲成直角的手臂的上半部分称为“勾”，下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.
1. 勾股定理揭示了直角三角形 之间的关系.
2. 根据勾股定理,已知直角三角形 边，可求 边.
在△ ABC中， ∠C =90°.⑴ 若a=3 , b=4 , 则 c= ⑵ 若b=7 , c=9 , 则 a=⑶ 若a=40 , c=41 , 则 b=
已知：在Rt △ ABC中，两直角边AC=5 , BC=12.求斜边上的高CD的长.
解：在Rt △ ABC中
求下列直角三角形中未知边的长.
求下列图中表示边的未知数x、y、z的值.
小明想知道旗杆的高度，他发现旗杆上的绳子垂到地面还多了2米，当他把绳子的下端拉开距旗杆底部8米时，发现绳子的末端刚好接触地面，求旗杆的高度.
解：如图所示，AB即为绳子的长度，AC为旗杆的高度.设旗杆高度为x米，在指教三角形ABC中，由勾股定理可得
答：旗杆高度为15米.
在Rt△ABC中， ∠C=90°,a,b为直角边，c为斜边，则有a2+b2=c2.
已知两边没有指明是直角边还是斜边时一定要分类讨论
1.Rt△ABC中，∠C=90°，若a=6，c=10，则b=____.
2.Rt△ABC中，∠C=90°，若a:b=3:4,c=10,则a=___，b=___.
3.Rt△ABC中，∠C=90°，若a=12，b=5，则斜边c上的高h= .
4.若直角三角形中，有两边长是5和7，则第三边长的平方为_________.
5.下列说法中,正确的是 （ ）A.已知a,b,c是三角形的三边，则a2+b2=c2B.在直角三角形中两边和的平方等于第三边的平方C.在Rt△ABC中，∠C=90°,所以a2+b2=c2D.在Rt△ABC中，∠B=90°,所以a2+b2=c2
6.图中阴影部分是一个正方形，则此正方形的面积为 .
7.在Rt△ABC中，AB＝4，AC＝3，求BC的长.
解：本题斜边不确定，需分类讨论：当AB为斜边时，如图，当BC为斜边时，如图，
8.如图，在△ABC中，AD⊥BC，∠B=45°，∠C=30°，AD=1，求△ABC的周长．
解：∵AD⊥BC，∴∠ADB=∠ADC=90°．在Rt△ADB中，∵∠B+∠BAD=90°，∠B=45°，∴∠B=∠BAD=45°，∴BD=AD=1，∴AB= ．在Rt△ADC中，∵∠C=30°，∴AC=2AD=2，∴CD= ，∴BC=BD+CD=1+ ，∴△ABC的周长=AB+AC+BC= ．