初中数学人教版（2024）七年级上册4.3.3 余角和补角同步练习题

这是一份初中数学人教版（2024）七年级上册4.3.3 余角和补角同步练习题，共40页。试卷主要包含了解答题等内容，欢迎下载使用。
1．已知：点O是直线AB上一点，过点O分别画射线OC，OE，使得．
（1）如图，OD平分．若，求的度数．请补全下面的解题过程（括号中填写推理的依据）．
解：∵点O是直线AB上一点，
∴．
∵，
∴．
∵OD平分．
∴（ ）．
∴ °．
∵，
∴（ ）．
∵ ，
∴ °．
（2）在平面内有一点D，满足．探究：当时，是否存在的值，使得．若存在，请直接写出的值；若不存在，请说明理由．
2．已知，与互余，与互补．
(1) 如图，当点B在的内，且点B、D在的同侧时．
①若，则________．
②若是的角平分线，则_______．（用含的式子表示）
直接写出所有可能的度数是_________．
3．如图，直线AB，CD相交于点O，OE平分，，
图中的余角是______把符合条件的角都填出来；
如果，那么根据______可得______度；
如果，求和的度数．
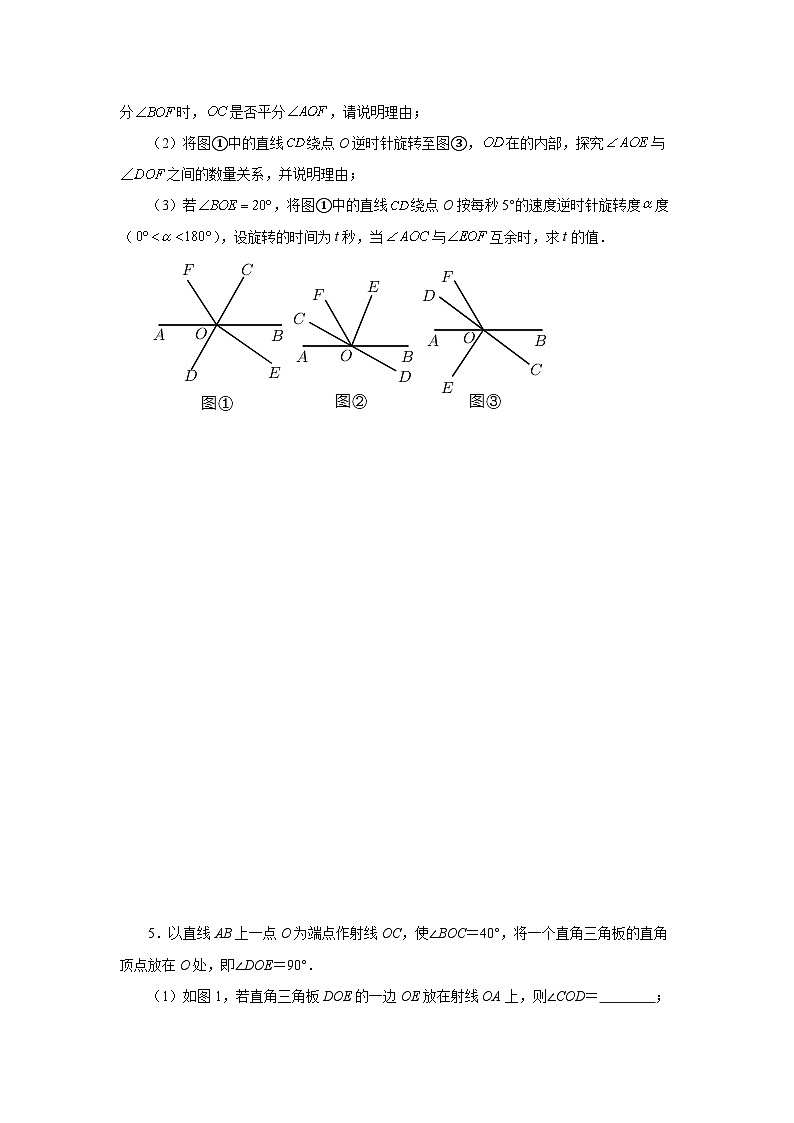
4．如图①，直线､相交于点O，射线，垂足为点O，过点O作射线使．
（1）将图①中的直线绕点O逆时针旋转至图②，在的内部，当平分时，是否平分，请说明理由；
（2）将图①中的直线绕点O逆时针旋转至图③，在的内部，探究与之间的数量关系，并说明理由；
（3）若，将图①中的直线绕点O按每秒5°的速度逆时针旋转度度（），设旋转的时间为t秒，当与互余时，求t的值．
5．以直线AB上一点O为端点作射线OC，使∠BOC＝40°，将一个直角三角板的直角顶点放在O处，即∠DOE＝90°．
（1）如图1，若直角三角板DOE的一边OE放在射线OA上，则∠COD＝ ；
（2）如图2，将直角三角板DOE绕点O顺时针转动到某个位置，若OE恰好平分∠AOC，则∠COD＝ ；
（3）将直角三角板DOE绕点O顺时针转动（OD与OB重合时为停止）的过程中，恰好有∠COD＝∠AOE，求此时∠BOD的度数．
6．若A、O、B三点共线，，将一个三角板的直角顶点放在点O处（注：，）．
(1) 如图1，使三角板的长直角边OD在射线OB上，则____________°；
(2) 将图1中的三角板DOE绕点O以每秒2°的速度按逆时针方向旋转到图2位置，此时，求运动时间的值；
(3) 将图2中的三角板DOE再绕点O以每秒5°的速度按顺时针转方向旋转一周，经过秒后，直线OC恰好平分，求的值．
7．阅读下面材料
小聪遇到这样一个问题：如图1，∠AOB＝α，请画一个∠AOC，使∠AOC与∠BOC互补．
小聪是这样思考的：首先通过分析明确射线OC在∠AOB的外部，画出示意图，如图2所示：然后通过构造平角找到∠AOC的补角∠COD．
如图3所示：进而分析要使∠AOC与∠BOC互补，则需∠BOC＝∠COD．
因此，小聪找到了解决问题的方法：反向延长射线OA得到射线OD，利用量角器画出∠BOD的平分线OC，这样就得到了∠BOC与∠AOC互补．
根据小聪的画法可知，如图3，点O在直线AD上，射线OC平分∠BOD．请说明∠AOC与∠BOC互补的理由；
参考小聪的画法，请在图4中画出一个∠AOH，使∠AOH与∠BOH互余（保留画图痕迹）；
已知∠EPQ和∠FPQ互余，射线PM平分∠EPQ，射线PN平分∠FPQ，若∠EPQ＝β（45°＜β＜90°），直接写出锐角∠MPN的度数是 ．
8．直观想象，逻辑推理
已知点O为直线AB上一点．
如图，过点O作射线OC，使，求与的度数；
如图，射线OC为内部任意一条射线，射线OD、OE分别是、的角平分线，求的度数，并写出简要的推理过程；
写出上图中所有互余的角和互补的角．
9．点O为直线AB上一点，将一直角三角板OMN的直角顶点放在点O处．射线OC平分∠MOB．
(1) 如图1，若∠AOM＝30°，求∠CON的度数；
(2) 在图1中，若∠AOM＝a，直接写出∠CON的度数（用含a的代数式表示）；
(3) 将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置，一边OM在射线OB上方，另一边ON在直线AB的下方．探究∠AOM和∠CON的度数之间的关系，写出你的结论，并说明理由．
10．将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起．
（1）若∠DCE=35°，则∠ACB的度数为_______；
（2）若∠ACB=144°42′，则∠DCE的度数为_______；
（3）猜想∠ACB与∠DCE的大小关系，并说明理由；
（4）三角尺ACD不动，将三角尺BCE的CE边与CA边重合，然后绕点C按顺时针或逆时针．方向任意转动一个角度，当∠ACE（0°＜∠ACE＜90°）等于多少度时，这两块三角尺各有一条边互相垂直，直接写出∠ACE角度所有可能的值是_______．(不用说明理由)
11．如图1，已知点为直线上一点，将一个直角三角板的直角顶点放在点处，并使边、边始终在直线的上方，平分．
（1）若，则__________°；
（2）若，求的度数（用含的代数式表示）；
（3）若在的内部有一条射线（如图2），满足，试确定与之间的数量关系，并说明理由．
12．如图，点O在直线AB上，．
（1）如图①，当的一边射线OC在直线AB上（即OC与OA重合），另一边射线OD在直线AB上方时，OF是的平分线，则的度数为_______．
（2）在图①的基础上，将绕着点O顺时针方向旋转（旋转角度小于），OE是的平分线，OF是的平分线，试探究的大小．
①如图②，当的两边射线OC、OD都在直线AB的上方时，求的度数．
小红、小英对该问题进行了讨论：
小红：先求出与的和，从而求出与的和，就能求出的度数．
小英：可设为x度，用含x的代数式表示、的度数，也能求出的度数．请你根据她们的讨论内容，求出的度数．
②如图③，当的一边射线OC在直线AB的上方，另一边射线OD在直线AB的下方时，小红和小英认为也能求出的度数．你同意她们的看法吗?若同意，请求出的度数；若不同意，请说明理由．
③如图④，当的两边射线OC、OD都在直线AB的下方时，能否求出的度数?若不能求出，请说明理由；若能求出，请直接写出的度数．
13．已知∠AOD=150°．
（1）如图1，∠AOC=∠BOD=90°，①∠BOC的余角是 ，比较∠AOB ∠COD（填＞，=或＜），理由： ；②∠BOC= 度；
（2）如图2，已知∠AOB与∠BOC互为余角，①若OB平分∠AOD，求∠BOC的度数；②若∠DOC是∠BOC的4倍，求∠BOC的度数．
14．点O在直线AB上，射线OC上的点C在直线AB上，．
（1）如图1，求∠AOC的度数；
（2）如图2，点D在直线AB上方，∠AOD与∠BOC互余，OE平分∠COD，求∠BOE的度数；
（3）在（2）的条件下，点F，G在直线AB下方，OG平分∠FOB，若∠FOD与∠BOG互补，求∠EOF的度数．
15．如图（1），将两块直角三角尺的直角顶点叠放在一起，
（1）若，则______；若，则______；
（2）①猜想与的大小有何特殊关系，并说明理由；
②应用：当的余角的4倍等于时，则是______度
拓展：如图（2），若是两个同样的直角三角尺锐角的顶点重合在一起，则与的大小又有何关系，直接写出结论不必证明．
16．已知：如图所示，OD平分∠BOC，OE平分∠AOC．若∠BOC=70°，∠AOC=50°．
（1）求出∠AOB及其补角的度数；
（2）求出∠DOC和∠AOE的度数，并判断∠DOE 与∠AOB是否互补，并说明理由；
（3）若∠BOC=α，∠AOC=β，则∠DOE 与∠AOB是否互补，并说明理由．
17．如图，直线AB与直线CD相交于点O，EO⊥AB，OF平分∠AOC，
（1）请写出∠EOC的余角 ；
（2）若∠BOC＝40°，求∠EOF的度数．
18．图（1）所示，点O是直线AB上一点，∠COD是直角，OE平分∠BOC．
(1) 若∠AOC＝30°，求∠DOE的度数；
(2) 将图（1）中的∠COD绕点O顺时针旋转至图（2）所示的位置，以（1）题思路探究∠AOC与∠DOE的度数之间的关系，并说明理由；
(3) 将图（1）中的∠COD绕点O顺时针旋转至图（3）所示的位置，直接写出∠AOC与∠DOE的度数之间的关系．
参考答案
1．（1）角平分线的定义；70；垂直的定义；DOC；EOC；160；（2）存在，的值为120°或144°或
【分析】（1）根据角平分线的定义和垂直定义，结合所给解题过程进行补充即可；
（2）分三种情况讨论：①点D，C，E在AB上方时，②当点D在AB的下方，C，E在AB上方时，③如图，当D在AB上方，E，C在AB下方时，用含有α的式子表示出和∠BOE，由列式求解即可．
解：（1）∵点O是直线AB上一点，
∴．
∵，
∴．
∵OD平分．
∴（ 角平分线的定义 ）．
∴ 70 °．
∵，
∴（ 垂直的定义 ）．
∵ DOC EOC ，
∴ 160 °．
故答案为：角平分线定义；70；垂直的定义；DOC；EOC；160；
（2）存在， 或144°或
①点D，C，E在AB上方时，如图，
∵，
∴
∵
∴
∵
∴
∴
②当点D在AB的下方，C，E在AB上方时，如图，
∵
∴
∵
∴
∴
∵
∴
∴
③如图，当D在AB上方，E，C在AB下方时，
同理可得：

，

解得：
综上，的值为120°或144°或
【点拨】本题主要考查角平分线和补角，熟练掌握角平分线的定义和补角的定义是解题的关键．
2．(1)①；②．(2)或．
【分析】（1）①根据与互余，得到，根据角的和差即可算出．②因为，与互补，所以根据角平分线的定义得到，根据角的和差即可求出的度数．
（2）注意分情况讨论：如图1：；如图2：；如图3：求出每种情况的角的度数，即为该题的答案．
(1)解：①
∵，与互余，
∴，
∵，
∴，
．
②∵，与互补
∴，
∵平分
∴，
∴
＝－
．
(2)解：如图1：
，，，
∴．
如图2：
如图3：
∴或．
【点拨】本题考查了余角和补角，角平分线的定义；解题的关键是利用了互余的定义，角平分线的定义以及角的和差进行计算．
3．（1）∠BOC、∠AOD（2）对顶角相等，160（3）26°
试题分析：（1）根据互余两角和为90°，结合图形找出即可；
（2）从图形中可知∠AOC和∠DOB为对顶角，直接可求解；
（3）根据角平分线可求∠AOD的度数，然后根据对顶角和邻补角可求解.
解：（1）图中∠AOF的余角是∠BOC、∠AOD（把符合条件的角都填出来）；
（2）如果∠AOC=160°，那么根据对顶角相等可得∠BOD=160度；
（3）∵OE平分∠AOD，
∴∠AOD=2∠1=64°，
∴∠2=∠AOD=64°，∠3=90°﹣64°=26°．
4．（1）平分，理由见解析；（2），理由见解析；（3）或时，与互余．
【分析】（1）根据平分线的定义可得，根据，可得，从而得到，所以可得结论；
（2）设为，根据可得，根据可得，从而得到与之间的数量关系；
（3）根据题意可知，因为，所以可得，可求出，根据“直线绕点O按每秒5°的速度逆时针旋转”可得出，，，，然后分情况进行讨论：①时，②时，③时，，从而得出结果．
解：（1）平分，理由如下：
∵且平分
∴
∵
∴
∴
∴
∴
即平分
（2），理由如下：
设为，则
∵
∴
∴
即
（3）∵且
∴
又∵
∴
∴
∵直线绕点O按每秒5°的速度逆时针旋转
∴①时，
若与互余，则
解得
②时，
若与互余，则
此时无解
③时，
若与互余，则
解得
综上所述，或时，与互余．
【点拨】本题考查了角的计算，角平分线有关的计算，余角相关计算．关键是认真审题并仔细观察图形，找到各个量之间的关系．
5．（1）50°；（2）20°；（3）15°或52.5°．
【分析】（1）利用余角的定义可求解；
（2）由平角的定义及角平分线的定义求解的度数，进而可求解；
（3）可分两种情况：①当在的内部时，②当在的外部时，根据角的和差可求解．
解：（1）由题意得，
，
，
故答案为；
（2），，
，
平分，
，
，
，
故答案为；
（3）①当在的内部时，
，而，
，
，，
，
又，
，
；
②当在的外部时，
，而，
，
，，
，
又，
，
，
综上所述：的度数为或．
【点拨】本题主要考查余角的定义，角的和差，角平分线的定义等知识的综合运用，分类讨论是解题的关键．
6．(1)50(2)25秒(3)11或47
【分析】（1）由余角的性质可求解；
（2）由角的数量关系列出等式可求解；
（3）分两种情况讨论即可.
（1）解：∵∠DOE＝90°，∠BOC＝40°，
∴∠COE=∠DOE-∠BOC＝90°-40°=50°，
故答案为：50；
（2）解：∵三角板DOE绕点O以每秒2°的速度按逆时针方向旋转，
∴经过t秒，∠COD=∠BOD-∠BOC=2t-40º，∠AOE=90º-2t，
∵，
∴2t-40º=（90º-2t），
解得t=25.
即运动时间为25秒.
（3）解：图2中∠AOE=90º-2t=40º，∠D1O E1=∠DOE=90º
∵三角板DOE再绕点O以每秒5°的速度按顺时针转方向旋转一周，
情况①如图：
经过秒后，∠EOE1=5t
∵直线OC恰好平分，
∴
∵∠BOC=40 º
∠AOC=∠AOE+∠EOE1+=140º
即40º+5t+45º=140º
解得：t=11；
情况②如图：
此时有：5t-10º-45º=180º，
解得t=47
故的值为11或47.
【点拨】本题考查了一元一次方程的应用，角平分线的定义，平角的性质等知识，熟练运用这些性质解决问题是本题的关键．
7．(1)理由见解析(2)见解析(3)45°或|β﹣45°|
【分析】（1）根据角平分线的定义可得∠BOC＝∠COD，根据等角的补角相等即可求得答案；
（2）先通过分析明确射线在的外部，作（或）的垂线，再利用量角器画出（或）的平分线即可得；
解：(1)如图3中，∵OC平分∠BOD，
∴∠BOC＝∠COD，
∵∠AOC+∠COD＝180°，
∴∠AOC+∠BOC＝180°，
即∠AOC与∠BOC互补；
(2)与互余，
，
，
射线在的外部，
先作（或）的垂线，再利用量角器画出（或）的平分线，如图所示：
或
(3)如图，
∵PM平分∠EPQ，PN平分∠FPQ，
∴∠MPQ＝∠EPQ，∠NPQ＝∠FPQ，
∵∠MPN＝∠MPQ+∠NPQ
＝∠EPQ+∠FPQ
＝∠EPF，
∵∠EPQ和∠FPQ互余，
∴∠EPQ+∠FPQ＝90°，
即∠EPF＝90°，
∴∠MPN＝45°；
如图：
∵PM平分∠EPQ，PN平分∠FPQ，
∴∠MPQ＝∠EPQ，∠NPQ＝∠FPQ，
∵∠MPN＝|∠MPQ﹣∠NPQ|＝|∠EPQ﹣∠FPQ|，
∵∠EPQ和∠FPQ互余，∠EPQ＝β，
∴∠FPQ＝90°﹣β，
∴∠MPN＝|β﹣∠（90°﹣β）|＝|β﹣45°|，
故答案为：45°或|β﹣45°|．
【点拨】本题考查了画垂线和角平分线、与角平分线有关的计算，较难的是题（3），正确分两种情况讨论是解题关键．
8．(1)∠AOC=108°，∠BOC=72°；(2)90°；过程见详解；(3)互余的角为：∠AOD和∠COE，∠AOD和∠EOB，∠DOC和∠COE，∠DOC和∠EOB；互补的角为：∠AOD和∠DOB，∠DOC和∠DOB，∠AOC和∠BOC，∠BOE和∠AOE，∠COE和∠AOE；
【分析】（1）设∠AOC=3x，∠BOC=2x，列方程求解即可；
（2）根据角平分线的定义，求∠DOC和∠COE的和即可；
（3）根据余角和补角的定义，等角的余角（补角）相等，结合图形解答；
(1)解：设∠AOC=3x，∠BOC=2x，由图可得：3x＋2x=180°，
5x=180°，
x=36°，
∴∠AOC=3×36°=108°，∠BOC=2×36°=72°；
(2)解：由题意可得：∠AOD=∠DOC=∠AOC，∠BOE=∠EOC=∠BOC，
∵∠AOC＋∠BOC=180°，
∴（∠AOC＋∠BOC）=90°，
∴∠DOC＋∠COE=90°，
∴∠DOE=90°；
(3)解：由（2）的条件和结论可得：
∵∠AOD＋∠COE=90°，∠AOD＋∠EOB=90°，∠DOC＋∠COE=90°，∠DOC＋∠EOB=90°，
∴互余的角为：∠AOD和∠COE，∠AOD和∠EOB，∠DOC和∠COE，∠DOC和∠EOB；
∵∠AOD＋∠DOB=180°，∠DOC＋∠DOB=180°，∠AOC＋∠BOC=180°，∠BOE＋∠AOE=180°，∠COE＋∠AOE=180°，
∴互补的角为：∠AOD和∠DOB，∠DOC和∠DOB，∠AOC和∠BOC，∠BOE和∠AOE，∠COE和∠AOE；
【点拨】此题考查了一元一次方程方程的应用，角平分线的定义（平分所在的角）；等角的余角（补角）；余角的定义：若两角和为90°则这两个角互余；补角的定义：若两角和为180°则这两个角互补；掌握定义结合图形是解题的关键．
9．(1)∠CON＝15°(2)∠CON＝a(3)∠CON＝∠AOM
【分析】（1）根据角平分线的定义和余角的性质即可得到结论；
（2）根据角平分线的定义和余角的性质即可得到结论；
（3）设∠AOM=a，则∠BOM=180°-a，根据角平分线的定义得到∠MOC=90°-α，根据余角的性质得到∠CON=α，于是得到结论．
（1）解：由已知得∠BOM=180°-∠AOM=150°，
又∠MON是直角，OC平分∠BOM，
所以∠CON=∠MON-∠BOM=90°-×150°=15°；
（2）解：由已知得∠BOM=180°-∠AOM=180°-α，
又∠MON是直角，OC平分∠BOM，
所以∠CON=∠MON-∠BOM=90°-×（180°-α）=α；
（3）解：∠AOM=2∠CON，
理由如下：
设∠AOM=，则∠BOM=180°-，
∵OC平分∠BOM，
∴∠MOC=∠BOM=（180°-）=90°-，
∵∠MON=90°，
∴∠CON=∠MON-∠MOC=90°-（90°-）=，
∴∠CON=∠AOM．
即∠AOM=2∠CON．
【点拨】本题主要考查了余角与补角，角的计算、角平分线的定义的运用，正确的理解题意是解题的关键．解题时注意方程思想的运用．
10．（1）145°；（2）35°18′；（3）∠ACB+∠DCE=180°；（4）30°、45°、60°、75°
【分析】（1）由于是两直角三角形板重叠，重叠的部分就比90°+90°减少的部分，所以若∠DCE=35°，则∠ACB的度数为180°-35°=145°．
（2）题与（1）正好相反，是已知重叠后的度数，因此若∠ACB=144°42′，则∠DCE的度数为180°-144°42′=35°18′．
（3）由于∠ACD=∠ECB=90°，重叠的度数就是∠ECD的度数，所以∠ACB+∠DCE=180°．
（4）分别利用CE⊥AD、EB⊥CD、BE⊥AD、CB⊥AD分别求出即可．
解：（1）∵∠ACD=∠ECB=90°，
∴∠ACB=180°-35°=145°．
（2）∵∠ACD=∠ECB=90°，
∴∠DCE=180°-144°42′=35°18′．
（3）∵∠ACE+∠ECD+∠DCB+∠ECD=180°，
∵∠ACE+∠ECD+∠DCB=∠ACB，
∴∠ACB+∠DCE=180°，即∠ACB与∠DCE互补．
（4）CE⊥AD时，
∠ACE=180°-90°-∠A=180°-90°-60°=30°；
EB⊥CD时，
∠E=∠ECD=45°，
∴∠ACE=∠ACD-∠ECD=45°，
BE⊥AD时，
∠CFB=∠DFE=180°-90°-30°=60°，
∴∠BCD=180°-∠B-∠CFB=75°，
∴∠ACE=∠BCD=75°；
CB⊥AD时，
∠ACB=180°-90°-∠A=30°，
∴∠ACE=90°-∠ACB=60°；
即∠ACE角度所有可能的值为：30°、45°、60°、75°．
【点拨】本题题主要考查了旋转的性质和互补、互余的定义等知识，解决本题的关键是理解重叠的部分实质是两个角的重叠．
11．（1）40；（2）2m°；（3）∠AOF+∠DOE=60°，理由见解析
【分析】（1）设∠AOC=x°，表示出∠BOD，∠COE，结合∠DOE列出方程，解之即可；
（2）同（1）的方法，将∠DOE=m°代入计算即可；
（3）根据OE平分∠BOC，得到∠COE=∠BOE，从而有2∠COE=3∠AOF+∠DOE，根据等量代换可得∠AOF+∠DOE=60°．
解：（1）由题意可得：∠COD=90°，
则∠AOC+∠BOD=90°，
设∠AOC=x°，则∠BOD=90°-x°，
∵OE平分∠BOC，
∴∠COE=∠BOE=∠BOC=（180°-x°）=90°-x°，
∵∠DOE=20°，
∴90°-x°-20°=90°-x°，
解得：x=40°，即∠AOC=40°；
（2）由题意可得：∠COD=90°，
则∠AOC+∠BOD=90°，
设∠AOC=x°，则∠BOD=90°-x°，
∵OE平分∠BOC，
∴∠COE=∠BOE=∠BOC=（180°-x°）=90°-x°，
∵∠DOE=m°，
∴90°-x°-m°=90°-x°，
解得：x=2m°，即∠AOC=2m°；
（3）∠AOF+∠DOE=60°．
∵OE平分∠BOC，
∴∠COE=∠BOE，
∵2∠BOE=3∠AOF+∠DOE，
∴2∠COE=3∠AOF+∠DOE，
∴2（∠COD-∠DOE）=3∠AOF+∠DOE，
2（90°-∠DOE）=3∠AOF+∠DOE，
180°-2∠DOE=3∠AOF+∠DOE，
3∠AOF+3∠DOE=180°，
∴∠AOF+∠DOE=60°．
【点拨】本题考查角平分线的意义，互为补角、互为余角的意义，牢固掌握相关性质并正确列式，是解题的关键．
12．（1）；（2）①；②同意，；③能求出，
【分析】（1）由得，再由角平分线的性质求出的度数，由即可求出结果；
（2）①根据小红和小英的方法，利用角的互补关系和角平分线的性质去求解角度；
②用同上的方法去求出结果；
③设，则，由角平分线的性质表示出和，根据即可求出结果．
解：（1）∵，
∴，
∵OF平分，
∴，
∴，
故答案是： ；
（2）①方法1：∵，
∴
∵OE平分，OF平分，
∴，，
∴，
∴，
方法2：设为x度，
∵OE平分，
∴，
∵，
∴，
∵OF平分，
∴，
∴；
②同意，
方法1：∵，OE平分，
∴，
∵，
∴，
∵OF平分，
∴，
∴，
方法2：设为x度，
∵OE平分，
∴，
∴，
∵，
∴，
∵OF平分，
∴，
∴，
③能求出，，理由：
设，则，
∴，
∵OE平分，OF平分，
∴，，
∴．
【点拨】本题考查角度求解，解题的关键是掌握角平分线的性质，角度互补和互余的性质．
13．（1）①∠AOB和∠COD，=，同角的余角相等；②30；（2）①15°；②∠BOC=15°
【分析】(1)①根据余角定义可得∠BOC的余角；利用同角的余角相等可得∠AOB=∠COD；
②首先计算出∠COD的度数，再根据余角定义可得∠BOC的度数；
(2)①根据余角定义可得∠AOC=90°， 然后根据角平分线定义可得∠ AOB的度数，再根据角的和差关系可得答案；
②首先计算出∠DOC的度数，然后再设∠BOC=，则∠DOC=4x°，进而可得4x=60，解方程即可.
解：（1）①∵∠AOC=∠BOD=90°，
∴∠BOC+∠AOB=90°，∠BOC+∠COD=90°，
∴∠BOC的余角是∠AOB和∠COD；
∴∠AOB=∠COD，
故答案为：∠AOB和∠COD，=，同角的余角相等；
②∵∠AOD=150°，∠AOC=90°，
∴∠COD=60°,
∵∠BOC+∠COD=90°，
∴∠BOC=30°，
故答案为：30；
（2）①∵∠AOB与∠BOC互为余角，
∠BOC+∠AOB=90°，
∵OB平分∠AOD，∠AOD=150°，
∴∠AOB=∠AOD=75°，
∴∠BOC=90°-∠AOB=15°；
②∵∠AOB与∠BOC互为余角，
∠BOC+∠AOB=90°，
∵∠AOD=150°，
∴∠COD=∠AOD-∠AOC=60°，
∵∠DOC是∠BOC的4倍，
∴设∠BOC=，则∠DOC=4x°，
∴4x=60，
解得x=15，
∴∠BOC=15°.
【点拨】此题考查余角和补角的定义，角平分线的定义，利用角平分线进行计算，角度的和差计算，正确掌握图形中各角度的关系是解题的关键.
14．（1）∠AOC=144°；（2）∠BOE =81°；（3）∠EOF =117°或171°
【分析】（1）设∠BOC=α，则∠AOC=4α，根据已知条件列方程即可得到结论；
（2）由余角的定义得到∠AOD=90°-∠BOC=90°-36°=54°，根据角平分线的定义得到∠COE=∠COD=×90°=45°，于是得到结论；
（3）①根据角平分线的定义得到∠FOG=∠BOG，设∠BOG=x°，∠BOF=2x°，∠BOD=∠DOC+∠BOC=36°+90°=126°，根据比较的定义列方程即可得到结论；
②根据角平分线的定义得到∠FOG=∠BOG，推出D，O，G共线，根据角的和差即可得到结论．
解：（1）设∠BOC=α，则∠AOC=4α，
∵∠BOC+∠AOC=180°，
∴α+4α=180°，
∴α=36°，
∴∠AOC=144°；
（2）∵∠AOD与∠BOC互余，
∴∠AOD=90°-∠BOC=90°-36°=54°，
∴∠COD=180°-∠AOD-∠BOC=180°-54°-36°=90°，
∵OE平分∠COD，
∴∠COE=∠COD＝×90°=45°，
∴∠BOE=∠COE+∠BOC=45°+36°=81°；
（3）①如图1，
∵OG平分∠FOB，
∴∠FOG=∠BOG，
∵∠FOD与∠BOG互补，
∴∠FOD+∠BOG=180°，
设∠BOG=x°，∠BOF=2x°，∠BOD=∠BOC+∠DOC =36°+90°=126°，
∵∠FOD=∠BOD+∠BOF，
∴126+2x+x=180，
解得：x=18，
∴∠EOF=∠BOE+∠BOF=81°+2×18°=117°；
②如图2，
∵OG平分∠FOB，
∴∠FOG=∠BOG，
∵∠FOD与∠BOG互补，
∴∠FOD+∠BOG=180°，
∴∠FOD+∠FOG=180°，
∴D，O，G共线，
∴∠BOG=∠AOD=54°，
∴∠AOF=180°-∠BOF=72°，
∴∠AOE=180°-∠BOE=180°-81°=99°，
∴∠EOF=∠AOF+∠AOE=72°+99°=171°．
【点拨】本题考查了余角和补角，角平分线的定义，补角的定义，正确的识别图形是解题的关键．
15．（1），；（2）①猜想得（或与互补），理由见解析；②30；（3）
【分析】（1）本题已知两块直角三角尺实际就是已知三角板的各个角的度数，根据角的和差就可以求出∠ACB，∠DCE的度数；
（2）①根据前两个小问题的结论猜想∠ACB与∠DCE的大小关系，结合前两问的解决思路得出证明；②根据①中的关系式以及的余角的4倍等于列出关于∠DCE的方程，求出∠DCE的度数，最后得出∠BCD的度数即可；
（3）根据（1）（2）解决思路确定∠DAB与∠CAE的大小并证明．
解：（1）∵∠ECB=90°，∠DCE=35°
∴∠DCB=90°-35°=55°
∵∠ACD=90°，
∴∠ACB=∠ACD+∠DCB=145°．
∵∠ACB=140°，
∴∠DCB=∠ACB-∠ACD=140°-90°=50°．
∴∠DCE=∠ECB-∠DCB=90°-50°=40°，
故答案为：145°，40°
（2）①猜想得∠ACB+∠DCE=180°（或∠ACB与∠DCE互补）
理由：∵∠ECB=90°，∠ACD=90°
∴∠ACB=∠ACD+∠DCB=90°+∠DCB
∠DCE=∠ECB-∠DCB=90°-∠DCB
∴∠ACB+∠DCE=180°．
②根据题意得，4（90°-∠DCE）=∠ACB，又由①得，∠ACB=180°-∠DCE，
∴4（90°-∠DCE）=180°-∠DCE，解得∠DCE=60°．
∴∠BCD=90°-∠DCE=30°．
故答案为：30°；
（3）∠DAB+∠CAE=120°．理由如下：
由于∠DAB=∠DAE+∠CAE+∠CAB，
故∠DAB+∠CAE=∠DAE+∠CAE+∠CAB+∠CAE=∠DAC+∠BAE=120°．
【点拨】此题考查了余角和补角、角的计算问题，解答本题的关键是仔细观察图形，根据图形得出各角之间的关系，难度一般．
16．（1）∠AOB=120°，其补角为60°；（2）∠DOE=60°，∠AOB=120°，∠DOE与∠AOB互补；（3）∠DOE与∠AOB不互补，理由见解析.
【分析】（1）由∠AOB=∠BOC+∠AOC，以及补角的定义，即可得到答案；
（2）根据角平分线的定义，即可求出∠DOE和∠AOE的度数，然后∠DOE+∠AOB=180°，即可得到答案；
（3）分别求出∠DOE与∠AOB的度数，然后进行判断，即可得到答案.
解：（1）∠AOB=∠BOC+∠AOC=70°+50°=120°，
其补角为：180°∠AOB=180°120°=60°．
（2）∠DOE与∠AOB互补；
理由如下：∵OD平分∠BOC，OE平分∠AOC，
∴∠DOC=∠BOC=×70°=35°，∠COE=∠AOC=×50°=25°．
∴∠DOE=∠DOC+∠COE =35°+25°=60°．
∴∠DOE+∠AOB=60°+120°=180°，
∴∠DOE与∠AOB互补．
（3）∠DOE与∠AOB不互补，
理由如下：∵OD平分∠BOC，OE平分∠AOC，
∴∠DOC=∠BOC=α，∠COE=∠AOC=β．
∴∠DOE=∠DOC+∠COE =α+β=（α+β）．
∴∠DOE+∠AOB=（α+β）+（α+β）=（α+β），
∴∠DOE与∠AOB不互补．
【点拨】本题考查了角平分线的定义，余角的定义，补角的定义，以及角的和差计算，解题的关键是熟练掌握几何图形中的角度的计算，熟练掌握所学的知识进行计算.
17．（1）∠BOC、∠AOD；（2）20°
【分析】（1）根据余角的定义、性质求得答案即可；
（2）根据补角的定义可计算出∠AOC＝180°﹣40°＝140°，再根据角平分线的定义可计算出∠FOC＝×140°＝70°，由垂直的定义得到∠EOB＝90°，则∠EOF＝90°﹣70°＝20°．
解：（1）∠EOC的余角有∠BOC、∠AOD；
（2）∵∠BOC＝40°，
∴∠AOC＝180°﹣40°＝140°，
∵OF平分∠AOC，
∴∠FOC＝×140°＝70°，
∵EO⊥AB，
∴∠EOB＝90°，
∴∠EOF＝90°﹣70°＝20°．
故答案为：∠BOC、∠AOD．
【点拨】本题考查了余角和补角：若两个角的和为90°，那么这两个互余；若两个角的和为180°，那么这两个互补．也考查了角平分线的定义．
18．(1)15°(2)(3)
【分析】（1）由已知可求出，再由是直角，平分求出的度数；
（2）由是直角，平分可得出，则得，从而得出和的度数之间的关系；
（3）根据（2）的解题思路，即可解答．
(1)解：由已知得∠AOC＝30°，则，
又是直角，平分，
，
故答案为：15°；
(2)解：；
理由：是直角，平分，
，
则得，
所以得：；
(3)解：；
理由：平分，
，
则得=，
所以得：．
【点拨】本题考查的知识点是角平分线的性质、几何图形中角的计算，解题的关键是正确运用有关性质准确计算角的和差倍分．