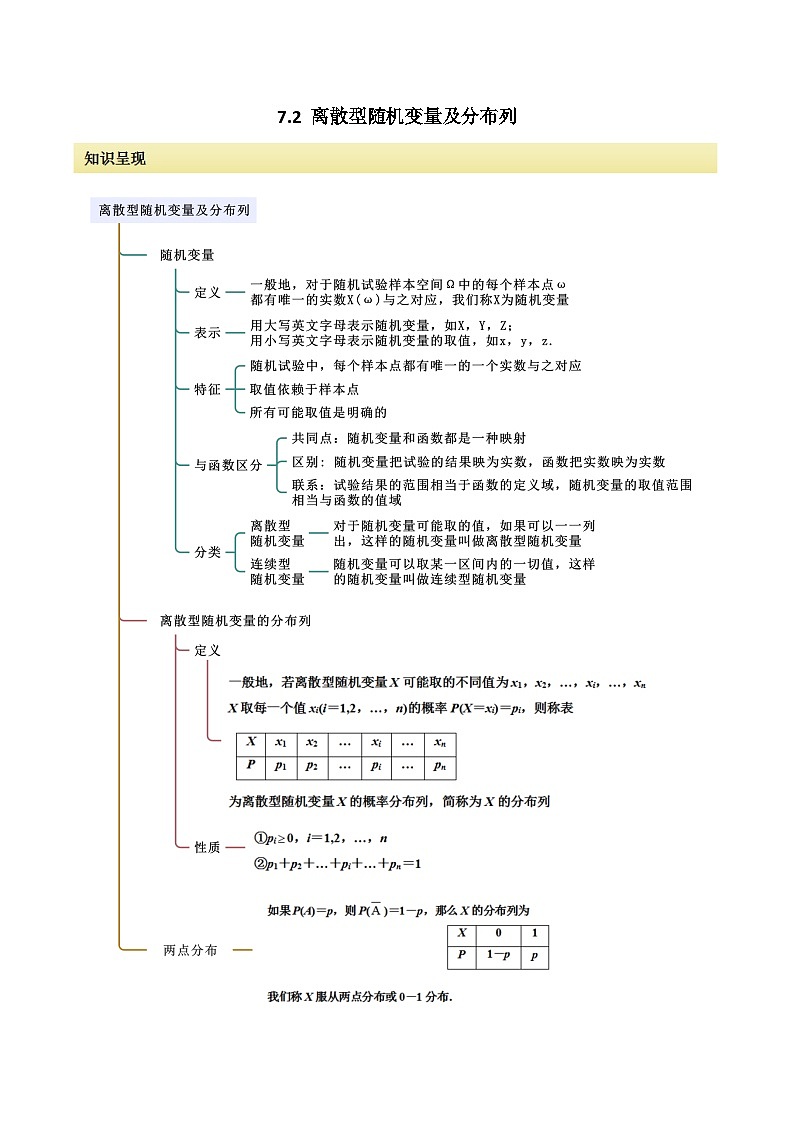
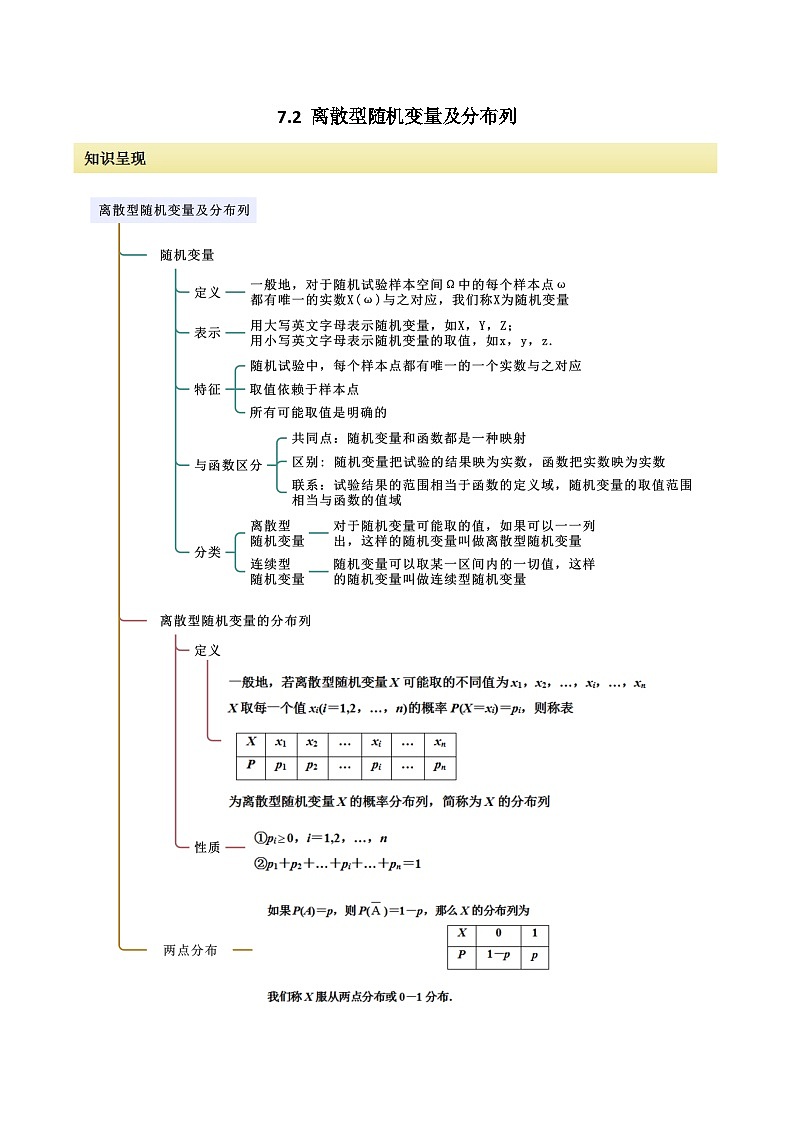
高中数学人教A版 (2019)选择性必修 第三册第七章 随机变量及其分布7.2 离散型随机变量及其分布列课时作业

这是一份高中数学人教A版 (2019)选择性必修 第三册第七章 随机变量及其分布7.2 离散型随机变量及其分布列课时作业，文件包含人教版高中数学选择性必修三精讲精练72离散型随机变量及分布列原卷版docx、人教版高中数学选择性必修三精讲精练72离散型随机变量及分布列解析版docx等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。


考法一 离散型随机变量的辨析
【例1】（2024安徽）（多选）下面给出四个随机变量，其中是离散型随机变量的为（ ）
A．高速公路某收费站在未来1小时内经过的车辆数X
B．一个沿直线进行随机运动的质点，它在该直线上的位置Y
C．某景点7月份每天接待的游客数量
D．某人一生中的身高X
【答案】AC
【解析】对于选项A：收费站在未来1小时内经过的车辆数X有限，且可一一列出，是离散型随机变量，故A正确
对于选项C：某景点7月份每天接待的游客数量有限，且可一一列出，是离散型随机变量，故C正确；
对于选项B、D，都是某一范围内的任意实数，无法一一列出，不符合离散型随机变量的定义，故B、D错误．
故选：AC.
【一隅三反】
1．（2023下·高二课时练习）（多选）下列随机变量中是离散型随机变量的是（ ）
A．一个袋中装有5个白球和5个黑球，从中任取3个，其中所含白球的个数
B．某林场的树木最高达30 m，则此林场中树木的高度
C．某加工厂加工的某种铜管的外径与规定的外径尺寸之差
D．某高中每年参加高考的人数
【答案】AD
【解析】对于A，从10个球中取3个球，所得的结果有以下几种：3个白球；2个白球和1个黑球；1个白球和2个黑球；3个黑球，即其结果可以一一列出，符合离散型随机变量的定义；
对于B，林场树木的高度是一个随机变量，它可以取（0，30]内的一切值，是连续型随机变量；
对于C，实际测量值与规定值之间的差值无法一一列出，是连续型随机变量；
对于D，每年参加高考的人数可一一列出，符合离散型随机变量的定义．
故选：AD
2．（2023福建）下列随机变量中不是离散型随机变量的是（ ）
A．掷5次硬币正面向上的次数M
B．从标有数字1至4的4个小球中任取2个小球，这2个小球上所标的数字之和Y
C．某人每天早晨在某公共汽车站等某一路车的时间T
D．将一个骰子掷3次，3次出现的点数之和X
【答案】C
【解析】在A中，掷5次硬币，正面向上的次数M可能取的值，可以按一定次序一一列出，故M是离散型随机变量
在B中，从标有数字1至4的4个小球中任取2个小球，这2个小球上所标的数字之和Y可能取的值，可以按一定次序一一列出，
故Y是离散型随机变量
在C中，某人每天早晨在某公共汽车站等某一路车的时间T可以取某一区间内的一切值，无法一一列出，
故T不是离散型随机变量
在D中，将一个骰子掷3次，3次出现的点数之和X可能取的值，可以按一定次序一一列出，故X是离散型随机变量
故选：C
3．（2023下·高二课时练习）下列随机变量中是离散型随机变量的是 ，是连续型随机变量的是 （填序号）．
①某机场候机室中一天的旅客数量X；
②某水文站观察到一天中江水的水位X；
③某景区一日接待游客的数量X；
④某大桥一天经过的车辆数X.
【答案】 ①③④ ②
【解析】①③④中的随机变量的所有取值，都可以按照一定的次序一一列出，因此它们是离散型随机变量；
②中的随机变量可以取某一区间内的一切值，故是连续型随机变量．
故答案为：①③④，②
考法二 离散型随机变量的分布列
【例2】（2024上·辽宁抚顺·高二校联考期末）某地要从2名男运动员､4名女运动员中随机选派3人外出比赛.
(1)若选派的3人中恰有1名男运动员和2名女运动员，则共有多少种选派方法？
(2)设选派的3人中男运动员与女运动员的人数之差为，求的分布列.
【答案】(1)种
(2)分布列见解析
【解析】（1）共有种选派方法.
（2）由题意知，的取值范围为，
，
所以的分布列为
【一隅三反】
1．（2023·全国·高二课堂例题）全班有40名学生，某次数学作业的成绩如下：
现从该班中任选一名学生，用X表示这名学生的数学作业成绩，求随机变量X的分布列．
【答案】答案见解析
【解析】由题意可得，，
，，
，．
因此，随机变量X的分布列是
2．（2023下·吉林长春·高二长春外国语学校校考期中）“绿水青山就是金山银山”，为推广生态环境保护意识，高二一班组织了环境保护兴趣小组，分为两组讨论学习.甲组一共有人，其中男生人，女生人；乙组一共有人，其中男生人，女生人.现要从这人的两个兴趣小组中抽出人参加学校的环保知识竞赛.
(1)设事件为“选出的这个人中，要求两个男生两个女生，而且这两个男生必须来自不同的组”，求事件发生的概率；
(2)用表示抽取的人中乙组女生的人数，求随机变量的分布列.
【答案】(1)
(2)分布列见解析
【解析】（1）.
（2）可能取值为，
，
，
，
，
的分布列为
3．（2024下·全国·高二随堂练习）设离散型随机变量X的分布列为
(1)求随机变量的分布列；
(2)求随机变量的分布列.
【答案】(1)分布列见解析
(2)分布列见解析
【解析】（1）由分布列的性质知：，解得，
列表为
即随机变量的可能取值为0，1，2，3，
可得，
，
，
故的分布列为
（2）列表得
即随机变量的可能取值为0，1，4，9，16.
从而的分布列为
考法三 分布列的性质
【例3-1】（2023·江西上饶）设随机变量X的分布列如下：
则p为（ ）．
A．B．C．D．
【答案】B
【解析】由分布列的性质可知，，得.
故选：B
【例3-2】（2023·安徽滁州）若随机变量的分布列为
则当时，实数的取值范围是（ ）
A．B．
C．D．
【答案】C
【解析】由随机变量的分布列知:
，
则当时，实数的取值范围是.
故选：C.
【一隅三反】
1．（2024·辽宁）设，随机变量的分布列为：
则（ ）
A．B．C．D．
【答案】D
【解析】由，得，
所以.
故选：D
2．（2022春·吉林长春·高二长春市第二实验中学校考期中）（多选）设随机变量的分布列为，（），则（ ）
A．B．
C．D．
【答案】ABC
【解析】选项A，由已知可得，，即，故该选项正确；
选项B，，故该选项正确；
选项C，，故该选项正确；
选项D，，故该选项错误.故选：ABC.
3（2023·全国·高二专题练习）设随机变量的分布列如下：
其中，，…，构成等差数列，则的最大值为___________.
【答案】
【解析】因为，，…，构成等差数列，所以，，
因为，所以，即，
所以，
所以当时，取得最大值.故答案为：
考法四 两点分布
【例4-1】（2023江苏）下列选项中的随机变量不服从两点分布的是（ ）
A．抛掷一枚骰子，所得点数
B．某射击手射击一次，击中目标的次数
C．从装有除颜色外其余均相同的5个红球，3个白球的袋中任取1个球，设
D．某医生做一次手术，手术成功的次数
【答案】A
【解析】对于选项A，抛掷一枚骰子，所得点数的取值范围为{1，2，3，4，5，6}，所以A中的随机变量不服从两点分布；
对于选项B，射击手射击一次，有击中或者不击中目标两种可能的结果，B中的随机变量服从两点分布；
对于选项C，袋中只有红球和白球，取出1个球，可能取到红球或者白球，C中的随机变量服从两点分布；
对于选项D，医生做一次手术，手术可能成功，也可能失败，D中的随机变量服从两点分布.
故选A.
【例4-2】．（2023·江西）从装有个白球和个红球的口袋中任取个球，用表示“取到的白球个数”，则的取值为或，即，求随机变量的概率分布．
【答案】分布列见解析
【解析】由题意知，，
故随机变量的概率分布列如下表所示：
【一隅三反】
1.（2023·全国·高二专题练习）（多选）下列选项中的随机变量服从两点分布的是（ ）．
A．抛掷一枚骰子，所得点数X
B．某射手射击一次，击中目标得2分，未击中目标得0分，射手的得分X
C．从装有5个红球，3个白球的袋子中取1个球，定义：“取出白球”，“取出红球”
D．某医生做一次手术，手术成功的次数X
【答案】CD
【解析】两点分布又叫0-1分布，试验结果只有两个，并且随机变量的取值只有0，1两个，C，D满足题意；
抛掷一枚骰子，所得点数X可能的结果为1，2，3，4，5，6，共6个，不是两点分布，A不满足题意；
某射手射击一次的试验结果有两个，但随机变量X的取值是0，2，B不满足题意．
故选：CD
2．（2023上·高二课时练习）在一次购物抽奖活动中，假设10张奖券中有一等奖奖券1张，可获价值50元的奖品，有二等奖奖券3张，每张可获价值10元的奖品，其余6张没有奖品．顾客甲从10张奖券中任意抽取1张，求中奖次数X的分布列．
【答案】分布列见解析
【解析】抽奖一次，只有中奖和不中奖两种情况，故X的取值只有1和0两种情况．
，
则.
因此X的分布列为：
3．（2023云南）袋中有除颜色外都相同的红球10个，白球5个，从中摸出2个球，如果只关心摸出两个红球的情形，问如何定义随机变量X，才能使X满足两点分布，并求分布列．
【答案】答案见解析
【解析】从含有10个红球，5个白球的袋中摸出2个球，其结果是随机的，可能是一红一白、两红、两白三种情况，为此我们定义随机变量如下：
当时，两个球非全红；当时，两个球全红.
则X显然服从两点分布，且，.
∴X的分布列为：
单选题
1．（2023·重庆）下表是离散型随机变量的分布列，则常数的值是（ ）
A．B．C．D．
【答案】C
【解析】由题意可得：，解得.
故选：C.
2．（2023山西）下列叙述中，是离散型随机变量的为（ ）
A．将一枚质地均匀的硬币掷五次，出现正面和反面向上的次数之和
B．某人早晨在车站等出租车的时间
C．连续不断地射击，首次命中目标所需要的次数
D．袋中有个黑球个红球，任取个，取得一个红球的可能性
【答案】C
【解析】对于A，掷硬币只有正面向上和反面向上两种结果，则掷五次，出现正面和反面向上的次数之和为，是常量，A错误；
对于B，等出租车的事件是随机变量，但无法一一列出，不是离散型随机变量，B错误；
对于C，连续不断地射击，首次命中目标所需要的次数是有限个或可列举的无限多个，是离散型随机变量，C正确；
对于D，事件发生的可能性不是随机变量，D错误.
故选：C.
3（2023山东）下列表中能称为随机变量X的分布列的是（ ）
A．
B．
C．
D．
【答案】C
【解析】对于A，由，故A错误；
对于B，由，故B错误；
对于C，由，故C正确；
对于D，由，故D错误.
答案：C
4．（2023下·高二课时练习）若随机变量的概率分布如下：
则当时，实数x的取值范围是（ ）
A．B．
C．D．
【答案】C
【解析】，，
当时，.
故选：C.
5．（2024上·山东德州·高二统考期末）离散型随机变量X的分布列中部分数据丢失，丢失数据以x，y（x，）代替，分布列如下：
则（ ）
A．0.35B．0.45C．0.55D．0.65
【答案】B
【解析】由题意得，化简得，
又且，所以，
所以.
故选：B
6．（2024甘肃）设离散型随机变量ξ的分布列如下表所示：
则下列各式正确的是（ ）
A． B．
C． D．
【答案】C
【解析】＋＋＋＝，A错误；
＋＝，B错误；
，C正确；
＋＝，D错误.
故选：C
7．（2023上·山东德州·高二校考阶段练习）如图，我国古代珠算算具算盘每个档挂珠的杆上有颗算珠，用梁隔开，梁上面颗叫上珠，下面颗叫下珠，若从某一档的颗算珠中任取颗，记上珠的个数为，则 （ ）
A．B．
C．D．
【答案】A
【解析】方法一：由题意可知，的所有可能取值为，，，
则．
方法二：由题意可知，的所有可能取值为，，，
则．
故选：A
8．（2023下·福建福州·高二校联考期中）已知随机变量的分布列为，2，3，，，则（ ）
A．B．C．D．
【答案】C
【解析】根据题意，随机变量的分布列为，
由分布列的性质，则有，解得，
故.
.
故选：C.
多选题
9．（2023上·高二课时练习）一个盒子里放着大小、形状完全相同的1个黑球、2个白球、2个红球，现不放回地随机从盒子中摸球，每次取一个，直到取到黑球为止，记摸到白球的个数为随机变量，则下列说法正确的是（ ）
A．B．
C．D．
【答案】CD
【解析】A选项，，分为第一次即取到黑球，
或第一次摸到红球，第二次摸到黑球，
或前两次均摸到红球，第三次摸到黑球，
故，A错误；
BC选项，，即第一次摸到白球，第二次摸到黑球，
或前两次一次摸到红球，一次摸到白球，第三次摸到黑球，
或前三次有两次摸到红球，一次摸到白球，第四次摸到黑球，
故，B错误，C正确；
D选项，的所有可能有，
故，D正确．
故选：CD.
10．（2023下·河南周口·高二校联考期中）已知离散型随机变量的分布列为
则下列选项正确的是（ ）
A．B．若，则
C．若，则D．
【答案】ABD
【解析】对于A中，由分布列的性质，可得，解得，所以A正确；
对于B中，若，可得，则，故B正确；
对于C中，由概率的定义知，所以C不正确；
对于D中，由，，则，所以D正确．
故选：ABD.
11．（2024湖北）下列选项中的随机变量服从两点分布的是（ ）．
A．抛掷一枚骰子，所得点数X
B．某射手射击一次，击中目标得2分，未击中目标得0分，射手的得分X
C．从装有5个红球，3个白球的袋子中取1个球，定义：“取出白球”，“取出红球”
D．某医生做一次手术，手术成功的次数X
【答案】CD
【解析】两点分布又叫0-1分布，试验结果只有两个，并且随机变量的取值只有0，1两个，C，D满足题意；
抛掷一枚骰子，所得点数X可能的结果为1，2，3，4，5，6，共6个，不是两点分布，A不满足题意；
某射手射击一次的试验结果有两个，但随机变量X的取值是0，2，B不满足题意．
故选：CD
12．（2023下·高二课时练习）抛掷两颗骰子各一次，记第一颗骰子掷出的点数与第二颗骰子掷出的点数的差为X，则“”表示的试验的结果有（ ）
A．第一颗为5点，第二颗为1点
B．第一颗大于4点，第二颗也大于4点
C．第一颗为6点，第二颗为1点
D．第一颗为6点，第二颗为2点
【答案】ACD
【解析】因为，
所以选项ACD符合题意，
对于选项B：第一颗大于4点，可以是5点，6点，
第二颗也大于4点，可以是5点，6点，
因为，
所以本选项不符合题意，
故选：ACD
填空题
13．（2023下·贵州遵义·高二统考期中）已知离散型随机变量X的分布列如表所示，则m的值为 .
【答案】/
【解析】依题意，，整理得，解得或，
当时，，，不符合题意，
当时，，，，，符合题意，
所以m的值为.
故答案为：
14．（2023下·新疆巴音郭楞·高二校考期末）袋中有大小相同的5个球，分别标有1，2，3，4，5五个号码，现在在有放回抽取的条件下依次取出两个球，设两个球号码之和为随机变量X，则X的可能取值是 ．（用集合表示）
【答案】
【解析】因为两球号码和可出现同号相加，如下表所示：
所以X的可能取值是.
故答案为：.
15．（2023广西）随机变量X的分布列为
若，，成等差数列，则公差的取值范围是______．
【答案】
【解析】由题意知，，
∴，∴．
又，∴，∴．
同理，由，，∴，
∴，即公差的取值范围是
故答案为：
16．（2024重庆）若随机变量X的分布列如下表所示：
则a2＋b2的最小值为________．
【答案】
【解析】由分布列的性质，知，即.
因为，当且仅当时取等号.
所以的最小值为.
故答案为：
解答题
17．（2023下·高二课时练习）写出下列各随机变量所有可能的取值，并说明随机变量所取的值表示的随机试验的结果．
(1)甲、乙两队员进行乒乓球单打比赛，规定采用“七局四胜制”，需要比赛的局数X；
(2)盒中装有6支白粉笔和2支红粉笔，从中任意取出3支，其中所含白粉笔的支数X，所含红粉笔的支数Y；
(3)在含有10件次品的100件产品中，任意抽取4件，其中含有次品的件数X.
【答案】(1)答案见解析
(2)答案见解析
(3)答案见解析
【解析】（1）根据题意可知X的可能取值为4，5，6，7.
表示“共打了4局，甲、乙两人有1人连胜4局”；
表示“在前4局中有1人输了1局，最后一局此人胜出”；
表示“在前5局中有1人输了2局，最后一局此人胜出”；
表示“在前6局中，两人打平，最后一局有1人胜出”．
（2）X的可能取值为1，2，3，表示“取出支白粉笔，支红粉笔”，其中；
Y的可能取值为0，1，2，表示“取出支红粉笔，支白粉笔”，其中.
（3）随机变量X的可能取值为0，1，2，3，4.
表示“取出的4件产品中有件次品”，其中.
18．（2024·江苏 ）某县教育局从县直学校推荐的6名教师中任选3人去参加进修活动，这6名教师中，语文、数学、英语教师各2人．
(1)求选出的数学教师人数多于语文教师人数的概率；
(2)设X表示选出的3人中数学教师的人数，求X的分布列．
【答案】(1)
(2)分布列见解析
【解析】（1）从6名老师中选3人的方法种数有：.
数学老师多于语文老师的选法有：
①1名数学，2名英语的选法：种；
②2名数学的选法有：种.
所以数学老师多于语文老师的选法有：种.
故数学老师多于语文老师的概率为：.
（2）由题意，的可能取值为：0，1，2.
，，.
所以的分布列为：
19（2024湖南）某食堂为了了解同学们在高峰期打饭的时间，故安排一名食堂阿姨随机收集了在食堂某窗口打饭的100位同学的相关数据(假设同学们打饭所用时间均为下表列出时间之一)，如下表所示.
已知这100位同学的打饭时间从小排到大的第65百分位数为17.5秒．
(1)确定x，y的值；
(2)若各学生的结算相互独立，记X为该窗口开始打饭至20秒末已经打饭结束的学生人数，求X的分布列．(注：将频率视为概率)
【答案】(1)
(2)分布列见解析
【解析】1）因为第65百分位数为17.5＝，所以，
所以.
（2）由已知得打饭时间为10秒的概率为，打饭时间为15秒的概率为，
打饭时间为20秒的概率为，打饭时间为25秒的概率为，
由题可知X的可能取值为0，1，2，
∴，，，
∴分布列如下：
20．（2024·湖南）某商店试销某种商品20天，获得如下数据：
试销结束后(假设该商品的日销售量的分布规律不变)，设某天开始营业时有该商品3件，当天营业结束后检查存货，若发现存量少于2件，则当天进货补充至3件，否则不进货，将频率视为概率.
（1）求当天商店不进货的概率；
（2）记X为第二天开始营业时该商品的件数，求X的分布列.
【答案】（1）；（2）答案见解析.
【解析】（1）记“当天商品销售量为0件”为事件A，“当天商品销售量为1件”为事件B，“当天商店不进货”为事件C，
则；
（2）由题意知，X的可能取值为2，3.
P(X＝2) ＝P(当天商品销售量为1件)＝；
P(X＝3)＝P(当天商品销售量为0件)＋P(当天商品销售量为2件)＋P(当天商品销售量为3件)
＝，
故X的分布列为：
21．（2024·广东佛山）一款击鼓小游戏的规则如下：每盘游戏都需击鼓三次，每次击鼓要么出现一次音乐，要么不出现音乐；每盘游戏击鼓三次后，出现一次音乐获得10分，出现两次音乐获得20分，出现三次音乐获得100分，没有出现音乐则扣除200分（即获得分）．设每次击鼓出现音乐的概率为，且各次击鼓出现音乐相互独立．
（1）若第一次击鼓出现音乐，求该盘游戏获得分的概率；
（2）设每盘游戏获得的分数为，求的分布列；
（3）玩三盘游戏，至少有一盘出现音乐的概率为多少？
【答案】（1）；（2）答案见解析；（3）．
【解析】】（1）若第一次击鼓出现音乐，则该盘游戏获得分的概率为：；
（2）可能的取值为，，，．根据题意，有
，，
，．
所以的分布列为：
（3）设“第盘游戏没有出现音乐”为事件（，则
．
所以“三盘游戏中至少有一盘出现音乐”的概率为：
．
因此，玩三盘游戏至少有一盘出现音乐的概率是．
22．（2024·湖南株洲）品酒师需要定期接受品酒鉴别能力测试，测试方法如下：拿出n瓶外观相同但品质不同的酒让其品尝，要求按品质优劣为它们排序，经过一段时间，等他等记忆淡忘之后，再让他品尝这n瓶酒，并重新按品质优劣为它们排序，这称为一轮测试.设在第一次排序时被排为1，2，3，…，n的n种酒，在第二次排序时的序号为，并令，称X是两次排序的偏离度.评委根据一轮测试中的两次排序的偏离度的高低为其评分.
(1)当时，若等可能地为1，2，3的各种排列，求X的分布列；
(2)当时，
①若等可能地为1，2，3，4的各种排列，计算的概率；
②假设某品酒师在连续三轮测试中，都有（各轮测试相互独立），你认为该品酒师的鉴别能力如何，请说明理由.
【答案】(1)答案见解析
(2)①；②答案见解析
【解析】（1）的排序共有种，且每种排序等可能，
此时可取，
又时，的排序为， ，
时，的排序为或，，
时，的排序为或或，，
所以的分布列为：
（2）①的排序共有种，且每种排序等可能，
而，故中有偶数个奇数，故必为偶数，
当时， 的排序与第一次排序无变化时，
此时仅有种排序：，则，
当时， 的排序与第一次排序相比仅有相邻两个位置变化时，
此时有种排序：、、，，
所以；
②因为各轮测试相互独立，
所以“连续三轮测试中，都有”的概率为，
所以是一个小概率，这表明仅凭随机猜测得到三轮测试都有的结果的可能性很小，
所以我们认为该品酒师有良好的鉴别能力，不是靠随机猜测.
-3
-1
1
分数
0
1
2
3
4
5
人数
0
1
3
12
20
4
X
0
1
2
3
4
5
P
0
0.025
0.075
0.3
0.5
0.1
0
1
2
3
X
0
1
2
3
4
P
0.2
0.1
0.1
0.3
m
X
0
1
2
3
4
1
0
1
2
3
η
0
1
2
3
P
0.1
0.3
0.3
0.3
X
0
1
2
3
4
0
1
4
9
16
0
1
4
9
16
P
0.2
0.1
0.1
0.3
0.3
X
1
2
3
4
P
p
X
0
1
2
3
P
0.1
0.2
0.1
0.3
0.1
0.2
5
8
9
1
2
3
4
5
6
P
0
1
X
0
1
P
X
0
1
P
X
3
4
5
9
P
X
－1
0
1
P
0.3
0.4
0.4
X
1
2
3
P
0.4
0.7
X
0
1
P
0.3
0.4
0.3
X
1
2
3
P
0.3
0.4
0.4
1
2
3
4
5
6
0.21
0.20
0.10
0.10
ξ
－1
0
1
2
3
P
1
2
4
6
0.2
0.1
0
1
2
3
一
二
1
2
3
4
5
1
2
3
4
5
6
2
3
4
5
6
7
3
4
5
6
7
8
4
5
6
7
8
9
5
6
7
8
9
10
X
P
X
0
1
2
3
P
a
b
0
1
2
0.2
0.6
0.2
学生数(人)
x
25
y
10
打饭时间(秒/人)
10
15
20
25
X
0
1
2
P
0.1
0.74
0.16
日销售量(件)
0
1
2
3
频数
1
5
9
5
X
2
3
P