高中数学人教A版 (2019)选择性必修 第三册7.2 离散型随机变量及其分布列教学课件ppt

课题

7.2《离散型随机变量的分布列》

教学目标

1.   知识目标

理解随机变量的意义；掌握离散型随机变量的概念；理解取有限值的离散型随机变量的分布列及两点分布的概念及表示；掌握离散型随机变量的分布列的性质；会求某些简单的离散型随机变量的分布列(含两点分布)。

2. 能力目标

知道随机变量的意义,区别随机变量与函数；能够写出随机变量的取值以及随机试验的结果；能够写出离散型随机变量的取值，会求离散型随机变量的分布列。

3. 情感目标

数学抽象：离散型随机变量的概念；逻辑推理：离散型随机变量与函数的关系；数学运算：会写出离散型随机变量；数学建模：离散型随机变量的表示。

教学重点

离散型随机变量的概念。

教学难点

结合实际问题写出随机变量的取值以及随机试验的结果，并求某些简单的离散型随机变量的分布列。

教学准备

1.          教师准备：课件
2.          学生准备：预习教材并完成资源与评价

教学过程

1. 复习导入：

1. 随机试验：

一般地，一个试验如果满足下列条件：

①试验可以在相同的情形下重复进行；

②试验的所有可能结果是明确可知的，并且不只一个；

③每次试验总是恰好出现这些可能结果中的一个，但在一次试验之前却不能肯定

这次试验会出现哪一个结果;

这种试验就是一个随机试验，为了方便起见，也简称试验。

2.函数：

一般地，设A，B是非空的数集，如果使对于集合A中的任意一个数x，按照某种确定的对应关系f，在集合B中都有唯一确定的数 y和它对应，那么就称f：A→B为从集合A到集合B的一个函数,记作:    

求随机事件的概率时，我们往往需要为随机试验建立样本空间，并会涉及样本点和随机事件的表示问题，类似函数在数集与数集之间建立对应关系，如果我们在随机试验的样本空间与实数集之间建立某种对应，将不仅可以为一些随机事件的表示带来方便，而且能更好地利用数学工具研究随机试验。 

问题：随机试验的样本空间与实数集之间能否建立某种对应关系呢？         

2. 新知探究：

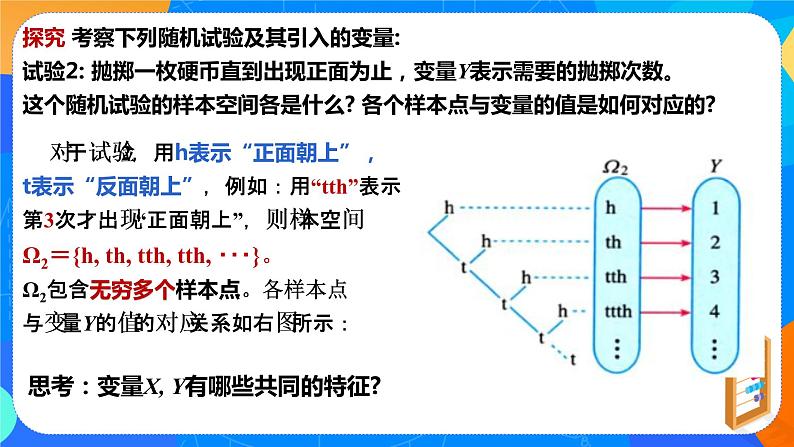
探究1：有些随机试验的样本空间与数值有关系，我们可以直接与实数建立关系。

（1）掷一枚骰子用实数?(?=1,2,3,4,5,6)表示“掷出的点数为?”。又如，掷两枚骰子样本空间为Ω={ (?,?) |?,?=1,2,⋯6},用?+?表示“两枚骰子的点数之和”，样本点(?,?)就与实数?+?对应。

（2）某射击运动员在射击训练中，其中某次射击可能出现命中的环数情况有哪些？实数?(?=0,1,2,3,4,5,6,···,10)表示“击中环数?”，（0环、1环、2环、···、10环）共11种结果。

探究2：有些随机试验的样本空间与数值没有关系，我们应该怎样与实数建立对应关系？

(1)随机抽取一件产品，有“抽到次品”和“抽到正品”两种可能结果它们与数值无关。如果“抽到次品”用1表示，“抽到正品”用0表示，即：

，这个试验的样本点与实数就建立了对应关系。

(2)掷一枚硬币,可将试验结果“正面朝上”用1表示，“反面朝上”用0表示。

(3)随机调查学生的体育综合测试成绩,可将等级成绩优、良、中等、及格、不及格分别赋值5.4.3.2.1，等等。对于任何一个随机试验，总可以把它的每个样本点与一个实数对应。

探究3：请同学们考察下列随机试验及其引入的变量，分析一下这两个随机试验的样本空间各是什么?各个样本点与变量的值是如何对应的?

试验1：从100个电子元件(至少含3个以上次品)中随机抽取三个进行试验，变量X 表示三个元件中次品数；

从100个电子元件(至少含3个以上次品)中随机抽取三个进行试验，变量X 表示三个元件中次品数；用0表示“元件为合格品”,1表示“元件为次品”,

用0和1构成的长度为3的字符串表示样本点，则样本空间：

Ω1={000,001,010,100,011,101,110,111}

：

      试验1图                    试验2图

试验2：抛掷一枚硬币直到出现正面为止，变量Y 表示需要的抛掷次数。

问题：两个试验中变量X,Y 有哪些共同的特征?

(1)取值依赖于样本点；(2)所有可能取值是明确的。

3. 新知讲授：

知识点1：随机变量的定义

。

知识点2：离散型随机变量的定义

练习1：写出下列各随机变量可能的取值，并说明随机变量所取值所表示的随机试验的结果：

(1)从10张已编号的卡片(从1号到10号)中任取1张，被取出的卡片的号数X ;

(2)一个袋中装有5个白球和5个黑球，从中任取3个，其中所含白球数X；

(3)抛掷两个骰子，所得点数之和X；

(4)接连不断地射击，首次命中目标需要的射击次数X ;

(5)某一自动装置无故障运转的时间X；

(6)某林场树木最高达30米，此林场树木的高度X 。

练习2：下列变量中是离散型随机变量的是？(1)(3)

(1)下期《诗词大会》节目中过关的人数；

(2)某加工厂加工的一批某种钢管的外径与规定的外径尺寸之差；

(3)在郑州至武汉的电气化铁道线上，每隔50 m有一电线铁塔，从郑州至武汉的电气化铁道线上将电线铁塔进行编号，其中某一电线铁塔的编号；

(4)江西九江市长江水位监测站所测水位在(0,29]这一范围内变化，该水位站所测水位。

探究4：抛掷一枚骰子,所得的点数X有哪些值？取每个值的概率是多少？

因为X取值范围是,而且。

因此X分布列如下表所示：

知识点3：离散型随机变量的分布列的概念

     一般地，设离散型随机变量X的可能取值为x1，x2，…，xn，我们称X取每一个值xi的概率：

为X的概率分布列，简称分布列。

与函数的表示法类似，离散型随机变量的分布列也可以用表格表示，还可以用图形来表示。下图直观的表示了掷骰子试验中掷出的点数X的分布列，成为X的概率分布图（见教材）。

知识点4：离散型随机变量的分布列的性质

(1) 

(2) 

利用分布列和概率的性质，可以计算由离散型随机变量表示的事件的概率。例如：在掷骰子的试验中，由概率加法公式，得事件“掷出的点数不大于2”的概率为：。

类似地，事件“掷出偶数点”的概率为

4. 例题精析：

例1 一批产品中次品率为5%,随机抽取1件,定义X ，。

解：

知识点5：两点分布（0-1分布）

对于只有两个结果的随机试验，用A表示“成功”，表示“失败”，定义

如果那么X的分布列如下表：

我们称X服从两点分布，或0——1分布。

实际上，X为在一次试验中成功(事件A发生)的次数(0或1)。像买彩票是否中奖，新生婴儿的性别，投篮是否命中，都可以用两点分布来描述。

例2某学校高二年级有200名学生,他们的体育综合测试成绩分5个等级,每个等级对应的分数和人数如下表所示。

从这200名学生中任意选取1人，求所选同学分数X的分布列以及。

解：由题意知，?是一个离散型随机变量，其可能取值为1,2,3,4,5,且{?=1}=“不及格”,{?=2}=“及格”, 。

根据古典概型的知识，可得?的分布列：

例3一批笔记本电脑共有10台，其中A品牌3台 ，B品牌7台。如果从中随机挑选2台，求这2台电脑中A品牌台数的分布列。

解：设挑选的2台电脑中?品牌的台数为?，则?的可能取值为0，1，2。根据古典概型的知识，可得?的分布列

用表格表示为：

5. 跟踪训练：

1．设离散型随机变量X的分布列为

若随机变量Y＝X－2，则P(Y＝2)等于(　　)

A．0．3　　　B．0．4  C．0．6           D．0．7

2．一批产品的次品率为5%，从中任意抽取一个进行检验，用随机变量X来描述次品出现的情况，即X＝0表示抽取的一个产品为合格品，X＝1表示抽取的一个产品为次品，则X的分布列为

则a＝________，b＝________．

3．将一枚骰子掷两次，求两次掷出的最大点数X的分布列.

6. 小结：

随机变量的概念——离散型随机变量的概念——离散型随机变量的分布列——离散型随机变量的性质——两点分布。

板书设计

  7.2离散型随机变量的分布列

1. 随机变量的定义：
2. 离散型随机变量的定义及其表示法：
3. 离散型随机变量的分布列及其性质：
4. 两点分布（0——1分布）：

课后作业

分层训练

课后反思

本节课的内容与必修2联系紧密，所以要先进行复习，让学生由一个思维上的一个准备。抽象随机变量的概念，主要依据是把随机试验的样本点与实数之间建立对应关系，学生还是比较容易接纳。由前面的掷骰子和掷硬币给出离散型随机变量的概念，这两个例子让学生对概念有个直观的认识。从而分布列概念及其性质的给出也不显得突兀。由例1给出两点分布的概念，更加的直观，又通过举例达到深化的效果。虽说知识点比较多，但是知识与知识之间的联系较为紧密，学生易于接受。