2025高考数学总复习专项复习（讲义）--概率专题六（含解析）

这是一份2025高考数学总复习专项复习（讲义）--概率专题六（含解析），共18页。学案主要包含了注意基础知识的整合，查漏补缺，保强攻弱，提高运算能力，规范解答过程，强化数学思维，构建知识体系，解题快慢结合，改错反思，重视和加强选择题的训练和研究等内容，欢迎下载使用。
一、注意基础知识的整合、巩固。进一步夯实基础，提高解题的准确性和速度。
二、查漏补缺，保强攻弱。针对“一模”的问题要根据自己的实际情况作出合理的安排。
三、提高运算能力，规范解答过程。一定要重视运算技巧粗中有细，提高运算准确性和速度。
四、强化数学思维，构建知识体系。同学们在听课时注意把重点要放到理解老师对问题思路的分析以及解法的归纳总结，以便于同学们在刷题时做到思路清晰，迅速准确。
五、解题快慢结合，改错反思。要适当地选择好的方案，解题动作要快要自信。
六、重视和加强选择题的训练和研究。对于选择题不但要答案正确，还要优化解题过程，提高速度。灵活运用特值法、排除法、数形结合法、估算法等。
人教A版数学--概率专题六
知识点一 写出简单离散型随机变量分布列,独立事件的乘法公式,求离散型随机变量的均值,
均值的实际应用
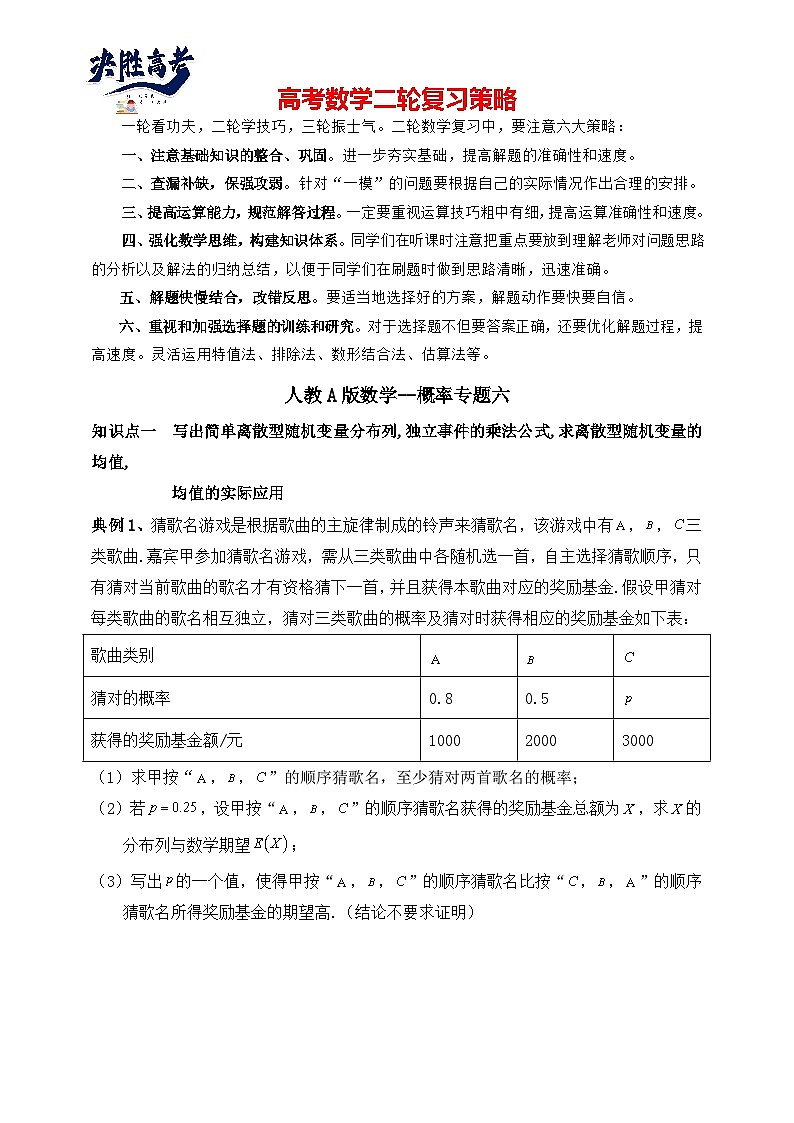
典例1、猜歌名游戏是根据歌曲的主旋律制成的铃声来猜歌名，该游戏中有，，三类歌曲.嘉宾甲参加猜歌名游戏，需从三类歌曲中各随机选一首，自主选择猜歌顺序，只有猜对当前歌曲的歌名才有资格猜下一首，并且获得本歌曲对应的奖励基金.假设甲猜对每类歌曲的歌名相互独立，猜对三类歌曲的概率及猜对时获得相应的奖励基金如下表：
（1）求甲按“，，”的顺序猜歌名，至少猜对两首歌名的概率；
（2）若，设甲按“，，”的顺序猜歌名获得的奖励基金总额为，求的分布列与数学期望；
（3）写出的一个值，使得甲按“，，”的顺序猜歌名比按“，，”的顺序猜歌名所得奖励基金的期望高.（结论不要求证明）
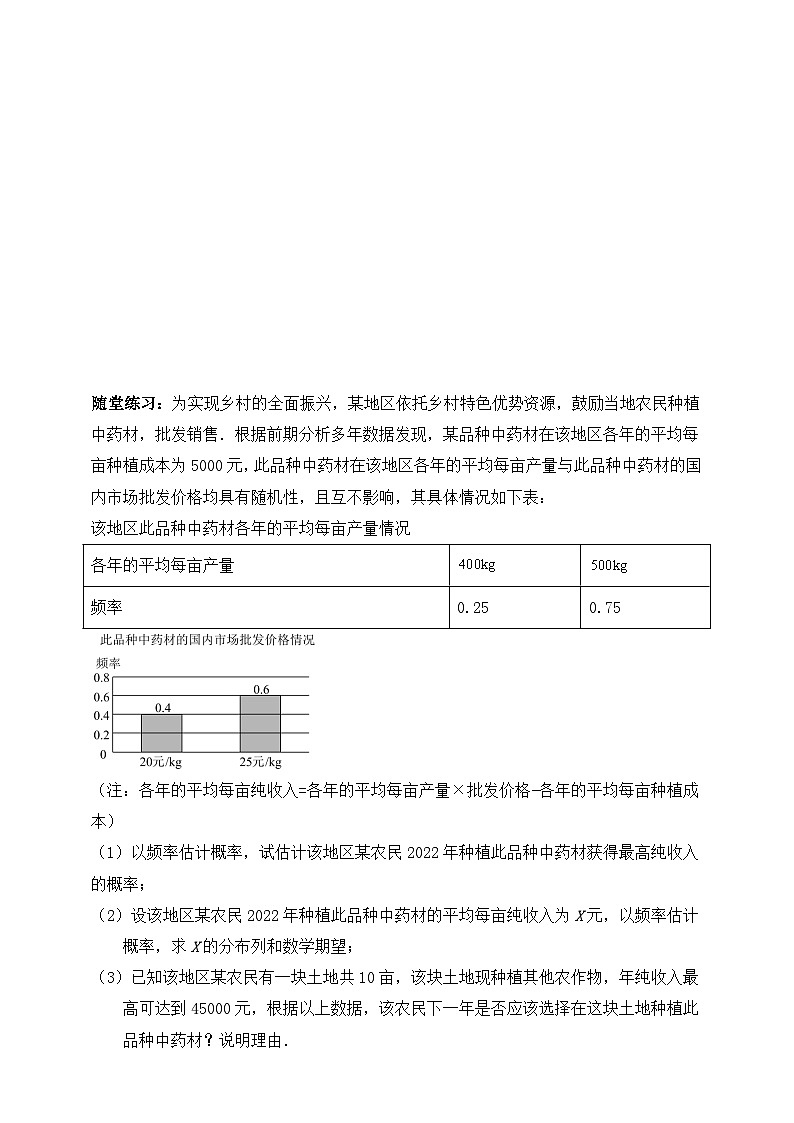
随堂练习：为实现乡村的全面振兴，某地区依托乡村特色优势资源，鼓励当地农民种植中药材，批发销售．根据前期分析多年数据发现，某品种中药材在该地区各年的平均每亩种植成本为5000元，此品种中药材在该地区各年的平均每亩产量与此品种中药材的国内市场批发价格均具有随机性，且互不影响，其具体情况如下表：
该地区此品种中药材各年的平均每亩产量情况
（注：各年的平均每亩纯收入=各年的平均每亩产量×批发价格-各年的平均每亩种植成本）
（1）以频率估计概率，试估计该地区某农民2022年种植此品种中药材获得最高纯收入的概率；
（2）设该地区某农民2022年种植此品种中药材的平均每亩纯收入为X元，以频率估计概率，求X的分布列和数学期望；
（3）已知该地区某农民有一块土地共10亩，该块土地现种植其他农作物，年纯收入最高可达到45000元，根据以上数据，该农民下一年是否应该选择在这块土地种植此品种中药材？说明理由．
典例2、自2019年底开始，一种新型冠状病毒COVID-19开始肆虐全球.人感染了新型冠状病毒后初期常见发热乏力、咽痛干咳、鼻塞流涕、腹痛腹泻等症状，严重者可致呼吸困难、脏器衰竭甚至死亡.筛查时可通过鼻拭子或咽拭子进行核酸检测判断.某定点医院对来院就诊的发热病人的鼻拭子进行化验，现A、B、C、D、E，F六人均出现了发热咳嗽等症状，经过初次鼻拭子化验已确定其中有且仅有一人罹患新冠肺炎，其余五人只是普通流感，但化验报告不慎遗失，现需要再次化验以确定六人中唯一的阳性患者的姓名.假设在接受化验的鼻拭子样本中每份样本是阳性结果是等可能的，且每份样本的检验结果是阳性还是阴性都是相互独立的.下面是两种化验方案：
方案甲：逐个化验，直到能确定患者为止；
方案乙：混合化验，先任取两人鼻拭子样本混合在一起化验，若混合样本化验结果呈阳性，则在这2人中任选一人进行化验；若结果呈阴性，则再任取两人鼻拭子样本混合重复第一次混合化验过程；若结果还是阴性，则在最后两份血样中任选一人进行化验；
（1）求方案甲所需化验次数的分布列及其期望.
（2）求方案甲所需化验次数不少于方案乙所需化验次数的概率.
随堂练习：首届以进口为主题的国家级博览会在中国拉开大幕，本次博览会包括企业产品展、国家贸易投资展．其中企业产品展分为7个展区，每个展区统计了备受关注百分比，如下表：
备受关注百分比指：一个展区中受到所有相关人士关注（简称备受关注）的企业数与该展区的企业数的比值．
（1）从企业产品展7个展区的企业中随机选取1家，求这家企业是选自“智能及高端装备”展区备受关注的企业的概率；
（2）从“消费电子及家电”展区备受关注的企业和“医疗器械及医药保健”展区备受关注的企业中，任选2家接受记者采访．记X为这2家企业中来自于“消费电子及家电”展区的企业数，求随机变量X的分布列．
典例3、中华猕猴桃果树喜湿怕旱，喜水怕涝，在我国种植范围较广.某地一生态农业公司建立了一个大型猕猴桃种植基地，该地区雨量充沛，阳光与温度条件也对果树的成长十分有利，但干旱或雨量过大也会造成损失.公司管理人员依据往年猕猴桃生长期30个周降雨量（单位：）的数据，得到如下茎叶图（表中的周降雨量为一周内降雨量的总和）.
另外，猕猴桃果树发生灾害与周降雨量的关系如下表所示.
根据上述信息，解答如下问题.
（1）根据茎叶图中所给的数据，写出周降雨量的中位数和众数；
（2）以收集数据的频率作为概率.
①估计该地区在今年发生重灾、轻灾以及无灾害的概率；
②若无灾害影响，每亩果树获利6000元：若受轻灾害影响，则每亩损失5400元；若受重灾害影响则每亩损失10800元.为保护猕猴桃产业的发展，该地区农业部门有如下三种防控方案；
方案1：防控到轻灾害，每亩防控费用400元.
方案2：防控到重灾害，每亩防控费用1080元.
方案3：不采取防控措施.
问：如从获利角度考虑，哪种方案比较好？说明理由.
随堂练习：近年来，新能源汽车受到越来越多消费者的青睐．据统计，2021年12月至2022年5月全国新能源市场三种车型月度零售销量数据如下（单位：万辆）：
（1）从2021年12月至2022年5月中任选1个月份，求该月零售销量超过这6个月该车型月度零售销量平均值的概率；
（2）从2022年1月至2022年5月中任选3个月份，将其中的月度零售销量相比上个月份增加的月份个数记为X，求X的分布列和数学期望；
（2）记2021年12月至2022年5月轿车月度零售销量数据的方差为，同期各月轿车与对应的 月度零售销量分别相加得到6个数据的方差为，写出与的大小关系．（结论不要求证明）
知识点二 计算几个数的平均数,计算古典概型问题的概率,独立事件的乘法公式
典例4、单板滑雪U型池比赛是冬奥会比赛中的一个项目，进入决赛阶段的12名运动员按照预赛成绩由低到高的出场顺序轮流进行三次滑行，裁判员根据运动员的腾空高度、完成的动作难度和效果进行评分.最终取每站三次滑行成绩的最高分作为该站比赛成绩.现有运动员甲、乙二人在2021赛季单板滑雪U型池世界杯分站比赛成绩如下表：
（1）从上表5站中随机选取一站，求在该站甲运动员的比赛成绩高于乙运动员的比赛成绩的概率；
（2）设甲乙成绩相互独立，从甲的5站比赛成绩和乙的5站比赛成绩中分别随机选取一个，求两人的比赛成绩中至少有一人高于88分的概率；
（3）甲5站的比赛成绩的平均值为，甲乙5站比赛成绩的总平均值记为，比较与的大小（直接写出结果）.
随堂练习：某学校组织“一带一路”知识竞赛，有A、B两类问题，每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答，若回答错误则该同学比赛结束：若回答正确则从另一类问题中再随机抽取一个问题回答，无论回答正确与否，该同学比赛结束．A类问题中的每个问题回答正确得20分，否则得0分；B类问题中的每个问题回答正确得80分，否则得0分．已知小明能正确回答A类问题的概率为0.8，能正确回答B类问题的概率为0.6，且能正确回答问题的概率与回答次序无关．
（1）若小明先回答B类问题，记Y为小明的累计得分，求的值；
（2）若小明先回答A类问题，记X为小明的累计得分，求X的分布列；
（3）为使累计得分的期望最大，小明应选择先回答哪类问题?请直接写出结论，不必说明理由．
典例5、某工厂两条生产线分别生产甲、乙两种元件，元件质量按测试指标划分为：指标大于或等于76为正品，小于76为次品.现分别从两条生产线随机抽取元件甲和元件乙各100件进行检测，检测结果统计如下：
（1）试分别估计生产一件元件甲、一件元件乙为正品的概率；
（2）生产一件元件甲，若是正品则盈利90元，若是次品则亏损10元；生产一件元件乙，若是正品则盈利100元，若是次品则亏损20元，则在（1）的前提下：
①求生产5件元件乙所获得的利润不少于300的概率；
②记X，Y分别为生产1000件元件甲和1000件元件乙所得的总利润，试比较和的大小.（结论不要求证明）
随堂练习：汽车租赁公司为了调查两种车型的出租情况，现随机抽取了这两种车型各100辆汽车，分别统计了每辆车某个星期内的出租天数，统计数据如下表：
（1）从出租天数为3天的汽车（仅限两种车型）中随机抽取一辆，估计这辆汽车恰好是A型车的概率；
（2）根据这个星期的统计数据（用频率估计概率），求该公司一辆型车，一辆型车一周内合计出租天数恰好为4天的概率；
（3）如果两种车型每辆车每天出租获得的利润相同，该公司需要从A，B两种车型中购买一辆，请你根据所学的统计知识，给出建议应该购买哪一种车型，并说明你的理由.
典例6、某超市从年甲、乙两种酸奶的日销售量（单位：箱）的数据中分别随机抽取个，并按、、、、分组，得到频率分布直方图如下：
假设甲、乙两种酸奶独立销售且日销售量相互独立.
（1）估计在未来的某一天里，甲、乙两种酸奶的销售量恰有一个高于箱且另一个不高于箱的概率；
（2）设表示在未来天内甲种酸奶的日销售量不高于箱的天数，以日销售量落入各组的频率作为概率，求的数学期望；
（3）记甲种酸奶与乙种酸奶口销售量（单位：箱）的方差分别为、，试比较与的大小（只需写出结论）.
随堂练习：为庆祝元旦，班委会决定组织游戏，主持人准备好甲､乙两个袋子.甲袋中有3个白球，2个黑球；乙袋中有4个白球，4个黑球.参加游戏的同学每抽出1个白球须做3个俯卧撑，每抽出1个黑球，须做6个俯卧撑
方案①：参加游戏的同学从甲､乙两个袋子中各随机抽出1个球；
方案②：主持人随机将甲袋中的2个球放入乙袋，然后参加游戏的同学从乙袋中随机抽出1个球；
方案③：主持人随机将乙袋中的2个球放入甲袋，然后参加游戏的同学从甲袋中随机抽出1个球.
（1）若同学小北选择方案①，求小北做6个俯卧撑的概率；
（2）若同学小北选择方案，设小北做俯卧撑的个数为，求的分布列；
（3）如果你可以选择按方案②或方案③参加游戏，且希望少做俯卧撑，那么你应该选择方案②还是方案③，还是两个方案都一样？（直接写出结论）
人教A版数学--概率专题六答案
典例1、答案：（1）0.4 （2）分布列见解析，期望为1900 （3）均可
解：（1）设“甲按“，，”的顺序猜歌名至少猜对两首歌名”为事件，
则.
所以，甲按“，，”的顺序猜歌名至少猜对两首歌名的概率为0.4.
（2）的所有可能取值为0，1000，3000，6000，
， ，
， .
所以随机变量的分布列为：
所以.
（3）证明：设甲按“，，”的顺序猜歌名所得奖励基金的总额为,
甲按“，，”的顺序猜歌名所得奖励基金的总额为
则的所有可能取值为0，3000，5000，6000，
， ，
， ，
所以，
则的所有可能取值为0，1000，3000，6000，

所以
要，即，
解得，因此均符合要求.
随堂练习：答案:（1）； （2）分布列见解析，期望为5925元； （3）应该，理由见解析.
解：（1）要使此品种中药材获得最高纯收入，则每亩产量和批发价格均要最高，
所以其概率为.
（2）由题意，每亩产量×批发价格-平均每亩种植成本，
每亩产量400千克，批发价格20元/千克：元；
每亩产量400千克，批发价格25元/千克：元；
每亩产量500千克，批发价格20元/千克：元；
每亩产量500千克，批发价格25元/千克：元；
所以X的可能值为，且，
，，
则X的分布列如下：
所以元.
（3）由（2）知：种植中药材的每亩期望年纯收入为5925元，
而种植其他农作物每亩年纯收入为4500元，
所以应该选择种植此品种中药材.
典例2、答案： （1）分布列见解析，期望为； （2）.
解：（1）的可能取值为，
，， ，
， ，
所以的分布列为：
所以；
（2）的可能取值为， ，，
所以
随堂练习：答案: （1）
（2）
解：（1）7个展区企业数共有家，
其中备受关注的智能及高端装备企业共家，
设从各展区随机选1家企业，这家企业是备受关注的智能及高端装备为事件，
所以.
（2）由表格可知：消费电子及家电备受关注的企业有家，
医疗器械及医药保健备受关注的企业有家，共家.
所以的可能取值为.
则；；.
所以随机变量的分布列为：
典例3、答案：（1）中位数为12.5，众数为10；（2）①估计该地在今年发生重、轻害的概率分别为和，无灾害概率为；②选择方案一比较好；答案见解析.
解: （1）根据茎叶图，可得中位数为12.5，众数为10
（2）①根据图中的数据，可得该地区周降雨量（单位：）的概率：
，，，，
（轻灾），（重灾）
因此估计该地在今年发生重、轻害的概率分别为和，无灾害概率为
②方案1：设每亩的获利为（元），则的可能取值为600，，则的分布列如下：
则（元），则每亩净利润为（元）；
方案2：设每亩的获利为（元），则的可能取值为6000元，于是，，净利润为（元）；
方案3：设每亩的获利为（元），则的可能取值为6000，，，
则的分布列如下：
则（元），于是每亩亏损为1400（元）；
由此得出，方案一的获利最多，所以选择方案一比较好.
随堂练习：答案: （1） （2）分布列见解析， （3）
解：（1）这6个月MPV车型月度零售销量平均值为
故MPV月度零售销量超过的月份为12月，4月，5月，
所以从2021年12月至2022年5月中任选1个月份，
该月MPV零售销量超过的概率为.
（2）从2022年1月至2022年5月，
SUV的月度零售销量相比上个月份增加的月份有2个：3月和5月，
所以的所有可能取值为，
则，
所以的分布列为
故的数学期望.
（3）依题意，2021年12月至2022年5月轿车月度零售销量分别为，
其平均值为，
所以轿车各月度零售销量与平均值的差约为，
所以，
同期各月轿车与对应的月度零售销量分别相加得到6个数据为：，
其平均值为，
所以轿车与对应的各月度零售销量与平均值的差为，
所以， 故.
典例4、答案： （1）； （2）； （3）