
2025高考数学总复习专项复习(讲义)--概率专题七(含解析)
展开一、注意基础知识的整合、巩固。进一步夯实基础,提高解题的准确性和速度。
二、查漏补缺,保强攻弱。针对“一模”的问题要根据自己的实际情况作出合理的安排。
三、提高运算能力,规范解答过程。一定要重视运算技巧粗中有细,提高运算准确性和速度。
四、强化数学思维,构建知识体系。同学们在听课时注意把重点要放到理解老师对问题思路的分析以及解法的归纳总结,以便于同学们在刷题时做到思路清晰,迅速准确。
五、解题快慢结合,改错反思。要适当地选择好的方案,解题动作要快要自信。
六、重视和加强选择题的训练和研究。对于选择题不但要答案正确,还要优化解题过程,提高速度。灵活运用特值法、排除法、数形结合法、估算法等。
人教A版数学--概率专题七
知识点一 写出简单离散型随机变量分布列,求离散型随机变量的均值,利用全概率公式求概率
典例1、某工厂生产一种航天仪器零件,每件零件生产成型后,得到合格零件的概率为0.6,得到的不合格零件可以进行一次技术处理,技术处理费用为100元/件,技术处理后得到合格零件的概率为0.5,得到的不合格零件成为废品.
(1)求得到一件合格零件的概率;
(2)合格零件以1500元/件的价格销售,废品以100元/件的价格被回收.零件的生产成本为800元/件,假如每件产品是否合格相互独立,记X为生产一件零件获得的利润,求X的分布列.
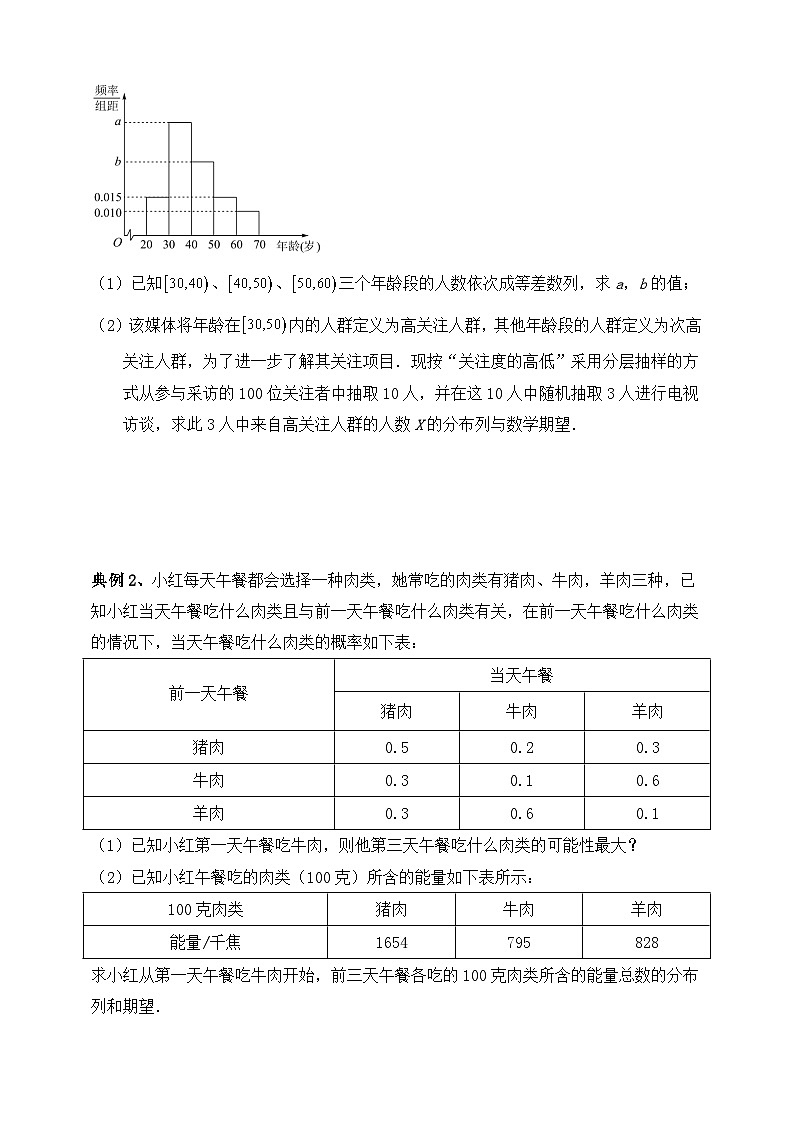
随堂练习:第24届冬季奥林匹克运动会于2022年2月4日在中国北京开幕,简称“北京冬奥会”.某媒体通过网络随机采访了某市100名关注“北京冬奥会”的市民,其年龄数据绘制成如图所示的频率分布直方图.
(1)已知、、三个年龄段的人数依次成等差数列,求a,b的值;
(2)该媒体将年龄在内的人群定义为高关注人群,其他年龄段的人群定义为次高关注人群,为了进一步了解其关注项目.现按“关注度的高低”采用分层抽样的方式从参与采访的100位关注者中抽取10人,并在这10人中随机抽取3人进行电视访谈,求此3人中来自高关注人群的人数X的分布列与数学期望.
典例2、小红每天午餐都会选择一种肉类,她常吃的肉类有猪肉、牛肉,羊肉三种,已知小红当天午餐吃什么肉类且与前一天午餐吃什么肉类有关,在前一天午餐吃什么肉类的情况下,当天午餐吃什么肉类的概率如下表:
(1)已知小红第一天午餐吃牛肉,则他第三天午餐吃什么肉类的可能性最大?
(2)已知小红午餐吃的肉类(100克)所含的能量如下表所示:
求小红从第一天午餐吃牛肉开始,前三天午餐各吃的100克肉类所含的能量总数的分布列和期望.
随堂练习:某学校有A,B,C三家餐厅,王同学每天晚餐时随机地选择其中一家餐厅用餐,已知他当天晚餐选择去哪家餐厅只与前一天晚餐去的餐厅有关,在前一天晚餐去某家餐厅的情况下,当天晚餐选择哪家餐厅的概率如下表:
(1)已知王同学第一天晚餐去了A餐厅,则他第三天晚餐去哪家餐厅的可能性最大?
(2)已知王同学在三家餐厅一天晚餐的消费金额如下表所示:求王同学从第一天晚餐去A餐厅开始,前三天的晚餐消费总金额的分布列和期望.
典例3、某商家为了促销,规定每位消费者均可免费参加一次抽奖活动,活动规则如下:在一不透明纸箱中有8张相同的卡片,其中4张卡片上印有“幸”字,另外4张卡片上印有“运”字.消费者从该纸箱中不放回地随机抽取4张卡片,若抽到的4张卡片上都印有同一个字,则获得一张10元代金券;若抽到的4张卡片中恰有3张卡片上印有同一个字,则获得一张5元代金券;若抽到的4张卡片是其他情况,则不获得任何奖励.
(1)求某位消费者在一次抽奖活动中抽到的4张卡片上都印有“幸”字的概率;
(2)记随机变量X为某位消费者在一次抽奖活动中获得代金券的金额数,求X的分布列和数学期望;
(3)该商家规定,消费者若想再次参加该项抽奖活动,则每抽奖一次需支付3元.若你是消费者,是否愿意再次参加该项抽奖活动?请说明理由.
随堂练习:2022年北京冬奥会后,由一名高山滑雪运动员甲组成的专业队,与两名高山滑雪爱好者乙、丙组成的业余队进行友谊比赛,约定赛制如下:业余队中的两名队员轮流与甲进行比赛,若甲连续赢两场则专业队获胜;若甲连续输两场则业余队获胜;若比赛三场还没有决出胜负,则视为平局,比赛结束.已知各场比赛相互独立,每场比赛都分出胜负,且甲与乙比赛,甲赢的概率为,甲与丙比赛,甲赢的概率为,其中.
(1)若第一场比赛,业余队可以安排乙与甲进行比赛,也可以安排丙与甲进行比赛.请分别计算两种安排下业余队获胜的概率;若以获胜概率大为最优决策,问:业余队第一场应该安排乙还是丙与甲进行比赛?
(2)为了激励专业队和业余队,赛事组织规定:比赛结束时,胜队获奖金6万元,负队获奖金3万元;若平局,两队各获奖金3.6万元.在比赛前,已知业余队采用了(1)中的最优决策与甲进行比赛,设赛事组织预备支付的奖金金额共计X万元,求X的数学期望的取值范围.
知识点二 绘制散点图,相关系数的意义及辨析,写出简单离散型随机变量分布列,
求离散型随机变量的均值
典例4、为了研究家用轿车在高速公路上的车速情况,交通部门随机对50名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在30名男性驾驶员中,平均车速超过的有20人,不超过的有10人.在20名女性驾驶员中,平均车速超过的有5人,不超过的有15人.
(1)完成下面的列联表,并判断是否有的把握认为平均车速超过的人与性别有关;
(2)以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随即抽取3辆,记这3辆车中驾驶员为女性且车速不超过的车辆数为,若每次抽取的结果是相互独立的,求的分布列和数学期望
参考公式:,其中.
参考数据:
随堂练习:某工厂为了提高生产效率,对生产设备进行了技术改造,为了对比技术改造后的效果,采集了技术改造前后各次连续正常运行的时间长度(单位:天)数据,整理如下:
改造前:;
改造后:.
(1)完成下面的列联表,并依据小概率值的独立性检验,分析判断技术改造前后的连续正常运行时间是否有差异?
(2)工厂的生产设备的运行需要进行维护,工厂对生产设备的生产维护费用包括正常维护费和保障维护费两种,对生产设备设定维护周期为天(即从开工运行到第天,)进行维护,生产设备在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产设备能连续运行,则只产生一次正常维护费,而不会产生保障维护费;若生产设备不能连续运行,则除产生一次正常维护费外,还产生保障维护费,经测算,正常维护费为万元/次,保障维护费第一次为万元/周期,此后每增加一次则保障维护费增加万元.现制定生产设备一个生产周期(以天计)内的维护方案:,.以生产设备在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及均值.
(其中)
典例5、中国在第75届联合国大会上承诺,将采取更加有力的政策和措施,力争于2030年之前使二氧化碳的排放达到峰值,努力争取2060年之前实现碳中和(简称“双碳目标”),此举展现了我国应对气候变化的坚定决心,预示着中国经济结构和经济社会运转方式将产生深刻变革,极大促进我国产业链的清洁化和绿色化.新能源汽车、电动汽车是重要的战略新兴产业,对于实现“双碳目标”具有重要的作用.为了解某一地区电动汽车销售情况,一机构根据统计数据,用最小二乘法得到电动汽车销量(单位:万台)关于(年份)的线性回归方程为,且销量的方差为,年份的方差为.
(1)求与的相关系数,并据此判断电动汽车销量与年份的相关性强弱;
(2)该机构还调查了该地区90位购车车主的性别与购车种类情况,得到的数据如下表:
依据小概率值的独立性检验,能否认为购买电动汽车与车主性别有关;
(3)在购买电动汽车的车主中按照性别进行分层抽样抽取7人,再从这7人中随机抽取3人,记这3人中,男性的人数为,求的分布列和数学期望.
①参考数据:;
②参考公式:(i)线性回归方程:,其中;
(ii)相关系数:,若,则可判断与线性相关较强.
(iii),其中.附表:
随堂练习:为了拓展城市的旅游业,实现不同市区间的物资交流,政府决定在市与市之间建一条直达公路,中间设有至少8个的偶数个十字路口,记为,现规划在每个路口处种植一颗杨树或者木棉树,且种植每种树木的概率均为.
(1)现征求两市居民的种植意见,看看哪一种植物更受欢迎,得到的数据如下所示:
是否有的把握认为喜欢树木的种类与居民所在的城市具有相关性;
(2)若从所有的路口中随机抽取4个路口,恰有个路口种植杨树,求的分布列以及数学期望;
(3)在所有的路口种植完成后,选取3个种植同一种树的路口,记总的选取方法数为,求证:.
附:
典例6、随着时代的不断发展,社会对高素质人才的需求不断扩大,我国本科毕业生中考研人数也不断攀升,2020年的考研人数是341万人,2021年考研人数是377万人.某省统计了该省其中四所大学2022年的毕业生人数及考研人数(单位:千人),得到如下表格:
(1)已知y与x具有较强的线性相关关系,求:y关于x的线性回归方程;
(2)假设该省对选择考研的大学生每人发放0.5万元的补贴.
①若该省大学2022年毕业生人数为8千人,估计该省要发放补贴的总全额:
②若大学的毕业生中小浙、小江选择考研的概率分别为,,该省对小浙、小江两人的考研补贴总金额的期望不超过0.75万元,求的取值范围.
参考公式:,.
随堂练习:某厂计划购买台机床,该种机床使用四年后即被淘汰,并且在使用过程中机床有一易损零件,若在购进机床同时额外购买这种易损零件作为备用件,此时每个只需元.在使用期间如果备件不足再购买,则每个要元.所以在购买前要决策购买数目.使得该厂购买机床时搭配的易损备用零件费用最省.为此业内相关人员先搜集了台以往这种机床在四年内更换的易损零件数,并整理数据后得如下柱状图.
以这台机床更换的易损零件数的频率代替每台机床更换的易损零件数发生的概率.记表示台机床四年内实际共需更换的易损零件数,表示购买台机床的同时备用的易损零件数目,为购买机床时备用件数发生的概率.
(1)求时的最小值;
(2)求的分布列及备用的易损零件数时的数学期望;
(3)将购买的机床分配给名年龄不同(视技术水平不同)的人加工一批模具,因熟练程度不同而加工出的产品数量不同,故产生的经济效益也不同.若用变量表示不同技工的年龄,变量为相应的效益值(元),根据以往统计经验,他们的每日工作效益满足最小二乘法和关于的线性回归方程,已知他们年龄的方差为,所对应的效益方差为.
①试预测年龄为岁的技工使用该机床每日所产生的经济效益;
②试根据的值判断使用该批机床的技工人员所产生的效益与技工年龄的相关性强弱.
附:下面三个计算回归直线方程的斜率和截距及表示随机变量与相关关系强弱的系数计算公式:,.
人教A版数学--概率专题七答案
典例1、答案:(1) (2)答案见解析
解:(1)设事件A:“一次性成型即合格”,设事件B:“经过技术处理后合格”,
则,.
所以得到一件合格零件的概率为.
(2)若一件零件一次成型即合格,则.
若一件零件经过技术处理后合格,则.
若一件零件成为废品,则. 所以可取,,,
则,,
,
所以随机变量的分布列为
随堂练习:答案: (1), (2)分布列见解析,1.8
解:(1)由题意可知 解得,.
(2)利用分层抽样从样本中抽取10人,
易知其中属于高关注人群的有人,
属于次高关注人群的有人.
则的所有可能取值为,,,,
所以,, ,
所以的分布列为:
所以.
典例2、答案:(1)小红第三午餐吃牛肉的可能性最大;(2)分布列见解析,期望为2978.677千焦.
解:(1)用A,B,C分别表示猪肉,牛内,羊肉三种肉类,
用,,分别表示第n天午餐小红A,B,C三种肉类的概率.
因为小红第一天午餐吃牛肉,
所以第2天午餐小红吃三种肉类的概率分别为,,.
第3天午餐小红吃三种肉类的概率分别为:,
,,
所以小红第三午餐吃牛肉的可能性最大.
(2)小红从第一天午餐吃牛肉开始,
前三天午餐的肉类安排有;BAA,BAB,BAC,BBA,BBB、BBC、BCA,BCB、BCC共9种,
所含的能量总数用X表示,有4103,3244,3277,2385,2418,2451共6种可能,
, ,
, ,
, .
所以小红从第一天午餐吃牛肉开始,前三天午餐各吃的100克肉类所含的能量总数X的分布列为
前三天午餐各吃的100克肉类所合的能量总数X的期望
(千焦)
所以小红从第一天午餐吃牛肉开始,
前三天午餐各吃的100克内其所合的能量总数X的期望为:2978.677千焦.
随堂练习:答案: (1)王同学第三天选择A餐厅的可能性最大(2)分布列见解析,期望为43.8元
解:(1)用,,分别表示第i天王同学选择A,B,C餐厅的概率,
因为王同学第一天去A,
所以第2天王同学选择A,B,C的概率分别为,,,
第3天王同学选择A,B,C的概率分别为,
, ,
所以王同学第三天选择A餐厅的可能性最大.
(2)王同学从第一天选择A餐厅开始,
前三天的选择有:AAA, AAB, AAC, ABA, ABB, ABC, ACA, ACB, ACC共9种,
由题得,消费总金额X的所有可能取值为35,40,45,50,55,
则:, ,
,
, ,
所以王同学从第一天去A餐厅开始,前三天消费总金额X(元)的分布列为
所以消费总金额X(元)的期望为
所以王同学从第一天晚餐去A餐厅开始,前三天的晚餐消费总金额X的期望为43.8元.
典例3、答案: (1) (2)分布列见解析, (3)不愿意,理由见解析
解:(1)记“某位消费者在一次抽奖活动中抽到的4张卡片上都印有“幸”字”为事件,
则,
所以某位消费者在一次抽奖活动中抽到的4张卡片上都印有“幸”字的概率为;
(2)依题意随机变量的所有可能取值为、、; 则,
, ,
所以的分布列为:
所以
(3)记随机变量为消费者在一次抽奖活动中的收益,则,
所以, 所以我不愿意再次参加该项抽奖活动;
随堂练习:答案: (1)安排乙 (2)
解:(1)第一场比赛,业余队安排乙与甲进行比赛,
业余队获胜的概率为:
第一场比赛,业余队安排丙与甲进行比赛,
业余队获胜的概率为:
因为,所以,
所以,业余队第一场应该安排乙与甲进行比赛.
(2)由已知万元,或万元
由(1)知,业余队最优决策是第一场应该安排乙与甲进行比赛.
此时,业余队获胜的概率为:
专业队获胜的概率为
所以,非平局的概率为
平局的概率为
X的分布列为:
X的期望为
由,所以数学期望的取值范围为(单位:万元)
典例4、答案:(1)有的把握 (2)
解:(1)
,所以有的把握认为平均车速超过与性别有关.
(2)根据样本估计总体的思想,从高速公路上行驶的大量家用轿车中随即抽取1辆,驾驶员为女性且车速不超过的车辆的概率为.
的可能取值为,且,
,
,
分布列为:
.
或.
随堂练习:答案:(1)列联表答案见解析,技术改造前后的连续正常运行时间有差异
(2)分布列答案见解析,均值为万元
解:(1)列联表为:
零假设:技术改造前后的连续正常运行时间无差异. ,
依据小概率值的独立性检验分析判断不成立,
即技术改造前后的连续正常运行时间有差异;
(2)由题知,生产周期内有4个维护周期,一个维护周期为30天,
一个维护周期内,生产线需保障维护的概率为,
设一个生产周期内需保障维护的次数为,则,
一个生产周期内的正常维护费为万元,保障维护费为万元,
一个生产周期内需保障维护次时的生产维护费为万元,
设一个生产周期内的生产维护费为,则的所有可能取值为,
所以,的分布列为
一个生产周期内生产维护费的均值为万元.
典例5、答案: (1),与线性相关较强
(2)认为购买电动汽车与车主性别有关,此推断犯错误的概率不大于
(3)分布列答案见解析,数学期望:
解:(1)相关系数为
故与线性相关较强.
(2)零假设为:购买电动汽车与车主性别相互独立,
即购买电动汽车与车主性别无关.
所以依据小概率值的独立性检验,我们推断不成立,
即认为购买电动汽车与车主性别有关,此推断犯错误的概率不大于.
(3)抽样比,男性车主选取2人,女性车主选取5人,则的可能取值为
故:,,
故的分布列为:
随堂练习:答案: (1)没有(2)分布列见解析,(3)证明见解析
解:(1)本次实验中,,
故没有99.9%的把握认为喜欢树木的种类与居民所在的城市具有相关性.
(2)依题意,的可能取值为0,1,2,3,4,
故, ,
故.
(3)∵,∴.要证,即证;
首先证明:对任意,有.
证明:因为,所以.
设个路口中有个路口种植杨树,
①当时,,
因为,所以, 于是.
②当时,,同上可得
③当时,,设,
当时,,
显然,当即时,,
当即时,,
即;,
因此,即. 综上,,即.
典例6、答案: (1) (2)① 300(万元);②
解:(1)由题意得,,
又,∴
∵,∴,
∴,所以,
故得y关于x的线性回归方程为.
(2)①将代入,
估计该省要发放补贴的总金额为(万元)
②设小浙、小江两人中选择考研的的人数为X,则X的所有可能值为0,1,2;
, ,
, ∴,
∴,解得,
又,∴,∴, 故p的取值范围为.
随堂练习:答案: (1);(2)分布列见解析,元;
(3)①元;②该机床的技工所产生的日经济效益与技工的年龄具有非常强的相关关系.
解:(1)根据图示柱表,易知更换易损零件的频数为的频率为.
易损零件的频数为的频率为.
将频率视为概率,且知每台机床易损零件的发生与否是相互独立的,
结合图表得:当时,;
当时,;
当时,;
当时,.
据互斥事件发生的概率知;
. 于是的最小值为;
(2)由(1)进而知,随机变量的可能取值为:、、、、、,
当时,;
当时,;
当时,.
于是分布列为:
进而结合(1)知,当备用的易损零件数时,随机变量取值为、、、、、,需注意的是,虽备用的易损零件数时,但发生的概率仍按实际需要的台机床时计算.
则购买易损零件所产生的实际费用数学期望为:
(元);
(3)①先根据回归方程易知(元),
即岁的技工日使用该机床产生的效益为元;
②由方差计算公式知,
即等价化为,
同理.
又,,,据公式求出相关系数
则有 .
易知:该机床的技工所产生的日经济效益与技工的年龄具有非常强的相关关系.
前一天午餐
当天午餐
猪肉
牛肉
羊肉
猪肉
0.5
0.2
0.3
牛肉
0.3
0.1
0.6
羊肉
0.3
0.6
0.1
100克肉类
猪肉
牛肉
羊肉
能量/千焦
1654
795
828
前一天
当天
A
B
C
A
0.1
0.6
0.3
B
0.4
0.2
0.4
C
0.5
0.3
0.2
餐厅
A
B
C
消费金额(元)
15
10
20
平均车数超过
人数
平均车速不超过
人数
合计
男性驾驶员人数
女性驾驶员人数
合计
0.150
0.100
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
技术改造
设备连续正常运行天数
合计
超过
不超过
改造前
改造后
合计
性别
购买非电动汽车
购买电动汽车
总计
男性
39
6
45
女性
30
15
45
总计
69
21
90
A市居民
B市居民
喜欢杨树
300
200
喜欢木棉树
250
250
0.100
0.050
0.010
0.001
2.706
3.841
6.635
10.828
大学
A大学
B大学
C大学
D大学
2022年毕业人数x(千人)
7
6
5
4
2022年考研人数y(千人)
0.5
0.4
0.3
0.2
0.6
0.2
0.2
X
3
2
1
0
P
X
4103
3244
3277
2385
2418
2451
P
0.15
0.09
0.27
0.01
0.42
0.06
X
35
40
45
50
55
P
0.12
0.3
0.34
0.18
0.06
X
9
7.2
平均车数超过
人数
平均车速不超过
人数
合计
男性驾驶员人数
20
10
30
女性驾驶员人数
5
15
20
合计
25
25
50
0
1
2
3
技术改造
设备连续正常运行天数
合计
超过
不超过
改造前
改造后
合计
0
1
2
0
1
2
3
4
2025高考数学总复习专项复习(讲义)--解三角形专题三(含解析): 这是一份2025高考数学总复习专项复习(讲义)--解三角形专题三(含解析),共6页。学案主要包含了注意基础知识的整合,查漏补缺,保强攻弱,提高运算能力,规范解答过程,强化数学思维,构建知识体系,解题快慢结合,改错反思,重视和加强选择题的训练和研究等内容,欢迎下载使用。
2025高考数学总复习专项复习(讲义)--解三角形专题七(含解析): 这是一份2025高考数学总复习专项复习(讲义)--解三角形专题七(含解析),共6页。学案主要包含了注意基础知识的整合,查漏补缺,保强攻弱,提高运算能力,规范解答过程,强化数学思维,构建知识体系,解题快慢结合,改错反思,重视和加强选择题的训练和研究等内容,欢迎下载使用。
2025高考数学总复习专项复习(讲义)--解三角形专题六(含解析): 这是一份2025高考数学总复习专项复习(讲义)--解三角形专题六(含解析),共8页。学案主要包含了注意基础知识的整合,查漏补缺,保强攻弱,提高运算能力,规范解答过程,强化数学思维,构建知识体系,解题快慢结合,改错反思,重视和加强选择题的训练和研究等内容,欢迎下载使用。












