2025高考数学总复习专项复习（讲义）--概率专题四（含解析）

这是一份2025高考数学总复习专项复习（讲义）--概率专题四（含解析），共19页。学案主要包含了注意基础知识的整合，查漏补缺，保强攻弱，提高运算能力，规范解答过程，强化数学思维，构建知识体系，解题快慢结合，改错反思，重视和加强选择题的训练和研究等内容，欢迎下载使用。
一、注意基础知识的整合、巩固。进一步夯实基础，提高解题的准确性和速度。
二、查漏补缺，保强攻弱。针对“一模”的问题要根据自己的实际情况作出合理的安排。
三、提高运算能力，规范解答过程。一定要重视运算技巧粗中有细，提高运算准确性和速度。
四、强化数学思维，构建知识体系。同学们在听课时注意把重点要放到理解老师对问题思路的分析以及解法的归纳总结，以便于同学们在刷题时做到思路清晰，迅速准确。
五、解题快慢结合，改错反思。要适当地选择好的方案，解题动作要快要自信。
六、重视和加强选择题的训练和研究。对于选择题不但要答案正确，还要优化解题过程，提高速度。灵活运用特值法、排除法、数形结合法、估算法等。
人教A版数学--概率专题四
知识点一 根据频率分布表解决实际问题,用频率估计概率,求离散型随机变量的均值
典例1、《中华人民共和国老年人权益保障法》规定，老年人的年龄起点标准是60周岁．为解决老年人打车难问题，许多公司均推出老年人一键叫车服务．某公司为调查老年人对打车软件的使用情况，在某地区随机抽取了100位老年人，调查结果整理如下：
（1）从该地区的老年人中随机抽取1位，试估计该老年人的年龄在且未使用过打车软件的概率；
（2）从参与调查的年龄在且使用过打车软件的老年人中，随机抽取2人进一步了解情况，用X表示这2人中年龄在的人数，求随机变量X的分布列及数学期望；
（3）为鼓励老年人使用打车软件，该公司拟对使用打车软件的老年人赠送1张10元的代金券，若该地区有5000位老年人，用样本估计总体，试估计该公司至少应准备多少张代金券．
随堂练习：近期，某中学全体学生参加了“全国节约用水大赛”活动．现从参加该活动的学生中随机抽取了男、女各25名学生，将他们的成绩（单位：分）记录如下：
（1）在抽取的50名学生中，从大赛成绩在80分以上的人中随机取出2人，求恰好男、女生各1名，且所在分数段不同的概率；
（2）从该校参加活动的男学生中随机抽取3人，设这3人中大赛成绩在80分以上的人数为X，求X的分布列和数学期望；
（3）试确定a、b为何值时，使得抽取的女生大赛成绩方差最小．（只写出结论，不需要说明理由）
典例2、某企业为了解职工款APP和款APP的用户量情况，对本单位职工进行简单随机抽样，获得数据如下表：
假设所有职工对两款APP是否使用相互独立.
（1）分别估计该企业男职工使用款APP的概率､该企业女职工使用款APP的概率；
（2）从该企业男，女职工中各随机抽取1人，记这2人中使用款APP的人数为，求的分布列及数学期望；
（3）据电商行业发布的市场分析报告显示，款APP的用户中男性占%､女性占%；款APP的用户中男性占%､女性占%.试分析该企业职工使用款APP的男､女用户占比情况和使用款APP的男､女用户占比情况哪一个与市场分析报告中的男､女用户占比情况更相符.
随堂练习：某调研机构就该市工薪阶层对“楼市限购令”的态度进行调查，抽调了5000名市民，他们月收入人数分布表和对“楼市限购令”赞成人数如下表：
（1）若从抽调的5000名市民中随机选取一名市民，求该市民赞成“楼市限购令”的概率；
（2）依据上表中的数据，若从该市工薪阶层随机选取两人进行调查，记赞成“楼市限购令”的人数为X,求X的分布列和数学期望；
（3）若从抽调的收入在(百元)的市民中随机抽取两名，记赞成“楼市限购令”的人数为，期望记作；若从抽调的收入在(百元)的市民中随机抽取两名，记赞成“楼市限购令”的人数为，期望记作，比较与的大小关系.(直接写出结论即可)
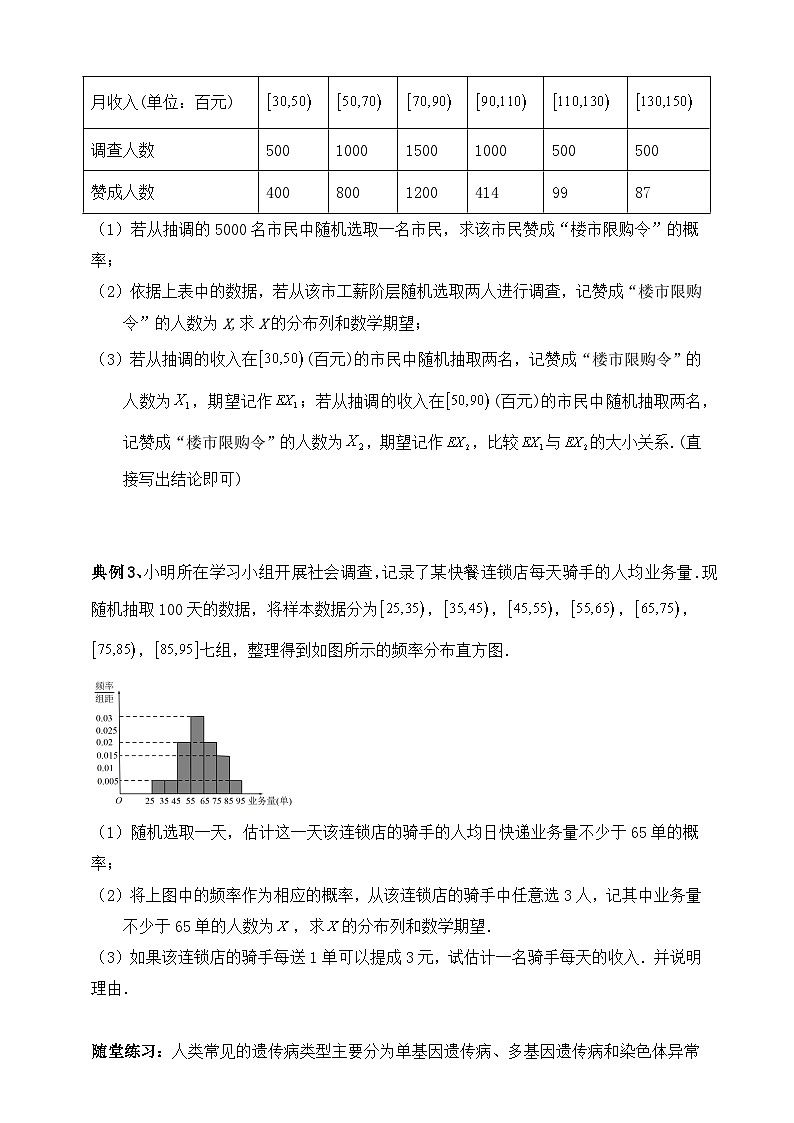
典例3、小明所在学习小组开展社会调查，记录了某快餐连锁店每天骑手的人均业务量．现随机抽取100天的数据，将样本数据分为，，，，，，七组，整理得到如图所示的频率分布直方图．
（1）随机选取一天，估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率；
（2）将上图中的频率作为相应的概率，从该连锁店的骑手中任意选3人，记其中业务量不少于65单的人数为，求的分布列和数学期望．
（3）如果该连锁店的骑手每送1单可以提成3元，试估计一名骑手每天的收入．并说明理由．
随堂练习：人类常见的遗传病类型主要分为单基因遗传病、多基因遗传病和染色体异常遗传病三大类，高度近视（600度以上）、红绿色盲都是较常见的单基因遗传病．某学校课后实践活动对学生这两种遗传病情况进行统计，分别从男、女同学中各随机抽取100人进行调查，对患病情况统计如下，其中“√”表示是，“×”表示否．
1、分别估计该校男生红绿色盲的发病率和该校女生红绿色盲的发病率；
2、为做家庭访问，从已调查出患红绿色盲的同学中任选两人，记这两人中男同学人数为，求的分布列及数学期望；
3、假设该校男生人数为1500，女生人数为2500，试估计该校学生高度近视发病率与该校学生红绿色盲发病率的大小关系，并说明理由．
（注：）
知识点二 独立性检验解决实际问题,计算条件概率
典例4、茶是中国颇受青睐的传统饮品．于爱茶的人而言，不仅迷恋于茶恬淡的气味与味道，泡茶工序带来的仪式感也是个修身养性静心的方式．但是细细品来，茶饮复杂的味型之中，总能品出点点的苦和淡淡的涩，所以也有人并不喜欢饮茶．在人们的固有印象中，总觉得中年人好饮茶，年轻人对饮茶持有怎样的态度呢？带着这样的疑问，高二3班的小明同学做了一项社会调查．调查针对身边的同学与方便联系的家长，共回收了200份有效问卷．为了提高统计工作的效率，小明只记录了问卷中三项有效数据，
（1）请将上面的信息表格补充完整（请在答题卡中画表格作答）；
（2）从这200人中随机选取2人，已知选取的2人中有人喜欢饮茶，求其中有学生的概率；
（3）请利用独立性检验相关的知识帮小明同学形成这次调查的结论．
公式：
随堂练习：在新冠肺炎疫情肆虐之初，作为重要防控物资之一的口罩是医务人员和人民群众抗击疫情的武器与保障，为了打赢疫情防控阻击战，我国企业依靠自身强大的科研能力，果断转产自行研制新型全自动高速口罩生产机，“争分夺秒、保质保量”成为口罩生产线上的重要标语．
（1）在试产初期，某新型全自动高速口罩生产流水线有四道工序，前三道工序完成成品口罩的生产且互不影响，第四道是检测工序，包括红外线自动检测与人工抽检．已知批次的成品口罩生产中，前三道工序的次品率分别为，．
①求批次I成品口罩的次品率．
②第四道工序中红外线自动检测为次品的口罩会被自动淘汰，合格的口罩进入流水线并由工人进行抽查检验.已知批次I的成品口罩红外线自动检测显示合格率为92%，求工人在流水线进行人工抽检时，抽检一个口罩恰为合格品的概率（百分号前保留两位小数）.
（2）已知某批次成品口罩的次品率为，设100个成品口罩中恰有1个不合格品的概率为，记的最大值点为，改进生产线后批次的口罩的次品率．某医院获得批次，的口罩捐赠并分发给该院医务人员使用．经统计，正常佩戴使用这两个批次的口罩期间，该院医务人员核酸检测情况如下面条形图所示，求，并判断是否有99.9%的把握认为口罩质量与感染新冠肺炎病毒的风险有关？
附：．
典例5、某种病菌在某地区人群中传播，目前临床医学研究中已有费用昂贵但能准确检测出个体是否带菌的方法.现引进操作易、成本低的新型检测方法：每次只需检测，两项指标，若指标的值大于4且指标的值大于100，则检测结果呈阳性，否则呈阴性.为考查该检测方法的准确度，随机抽取50位带菌者（用“*”表示）和50位不带菌者（用“”表示）各做一次检测，他们检测后的数据，制成统计图：
（1）从这100名被检测者中，随机抽取一名不带菌者，求检测结果呈阳性的概率；
（2）完成下列列联表，并判断能否在犯错误概率不超过0.001的前提下，认为“带菌”与“检测结果呈阳性”有关？
（参考公式：，其中）
随堂练习：根据国家电影局发布的数据，2020年中国电影总票房为204.17亿，年度票房首度超越北美，成为2020年全球第一大电影市场.国产历史战争题材影片《八佰》和《金刚川》合力贡献了国内全年票房的.我们用简单随机抽样的方法，分别从这两部电影的购票观众中各随调查了100名观众，得到结果如下：图1是购票观众年龄分布情况；图2是购票观众性别分布情况.
（1）记表示事件：“观看电影《八佰》的观众年龄低于30岁”，根据图1的数据，估计的概率；
（2）现从参与调查的电影《金刚川》的100名购票观众中随机抽取两名依次进行电话回访，求在第1次抽到男性观众的条件下，第2次仍抽到男性观众的概率.
（3）填写下面的列联表，并根据小概率值的独立性检验，分析男性观众与女性观众对这两部历史战争题材影片的选择是否有差异？
附：
典例6、大型综艺节目《最强大脑》中，有一个游戏叫做盲拧魔方，就是玩家先观察魔方状态并进行记忆，记住后蒙住眼睛快速还原魔方，盲拧在外人看来很神奇，其实原理是十分简单的，要学会盲拧也是很容易的.根据调查显示，是否喜欢盲拧魔方与性别有关.为了验证这个结论，某兴趣小组随机抽取了50名魔方爱好者进行调查，得到的情况如下表所示：
表（1）
并邀请其中20名男生参加盲拧三阶魔方比赛，其完成情况如下表（2）所示.
表（2）
（1）将表（1）补充完整，并判断能否在犯错误的概率不超过0.025的前提下认为是否喜欢盲拧与性别有关？
（2）现从表（2）中成功完成时间在和这两组内的6名男生中任意抽取2人对他们的盲拧情况进行视频记录，求2人成功完成时间恰好在同一组内的概率.
附参考公式及参考数据：，其中.
随堂练习：某手机商家为了更好地制定手机销售策略，随机对顾客进行了一次更换手机时间间隔的调查.从更换手机的时间间隔不少于3个月且不超过24个月的顾客中选取350名作为调查对象，其中男性顾客和女性顾客的比为，商家认为一年以内（含一年）更换手机为频繁更换手机，否则视为未频繁更换手机.现按照性别采用分层抽样的方法从中抽取105人，并按性别分为两组，得到如下表所示的频数分布表：
（1）计算表格中x，y的值；
（2）若以频率作为概率，从已抽取的105名且更换手机时间间隔为3至6个月（含3个月和6个月）的顾客中，随机抽取2人，求这2人均为男性的概率；
（3）请根据频率分布表填写列联表，并判断是否有以上把握认为“频繁更换手机与性别有关”.
附表及公式：
人教A版数学--概率专题四答案
典例1、答案： （1） （2）分布列见解析， （3）3900张
解：（1）在随机抽取的100位老年人中，年龄在且未使用过打车软件的人数为，
所以随机抽取的这1位老年人的年龄在且未使用过打车软件的概率．
（2）由题可知，X的所有可能取值为0，1，2，
且， ， ．
所以X的分布列为
故X的数学期望．
（3）在随机抽取的100位老年人中，使用过打车软件的共有（人），
所以估计该公司至少应准备张代金券．
随堂练习：答案： （1）；（2）分布列见解析；期望为；（3）．
解：（1）设“从大赛成绩在以上的人中随机取出2人，恰好男、女生各1名，且所在分数段不同”为事件A，
由表格可得：随机抽取的50名学生中，成绩在80分以上的男生人数是10人，女生5人，共15人，即从15名学生中随机抽取2人，所以样本空间；如果这2人恰好男、女生各1名，且分数段不同，即．所以事件A包含21个样本点，因此．
（2）由数据可知，从抽取的25名男学生中随机抽取1人，该学生大赛成绩在80分以上的概率为．即从该校参加活动的男学生中随机抽取1人，该学生大赛成绩在80分以上的概率为，因此从该校参加活动的男学生中随机抽取3人，这3人中大赛成绩在以上的人数可取，且．
，，，．
所以随机变量的分布列
数学期望 或者，所以．
（3） （由题意可得，由于方差是衡量一组数据的离散程度，当数据越集中，方差越小，所以时，数据更集中，方差最小）
典例2、答案：（1）；（2）分布列答案见解析，数学期望：；
（3）该企业职工使用APP的情况与官方发布的男､女用户情况更相符
解：（1）由所给数据可知，男职工使用A款APP的人数为72，
用频率估计概率，可得男职工使用京东APP的概率约为，
同理，女职工使用A款APP的概率约为；
（2）的可能取值为0，1，2，
；
；
.
的分布列为：
的数学期望；
（3）样本中，款APP的男､女用户为(人)，
其中男用户占%；女用户占%，
样本中，款APP的男､女用户为(人)，
其中男用户占%；女用户占%，
该企业职工使用APP的情况与官方发布的男､女用户情况更相符.
随堂练习：答案： （1） ；（2）分布列见详解，数学期望为；（3）；
解:（1）由数据可知，在抽调的5000名市民中， 有名，
由频率估计为概率，所以从抽调的5000名市民中随机选取一名市民，
该市民赞成“楼市限购令”的概率为，
（2）由（1）知，市民赞成“楼市限购令”的概率为，
记赞成“楼市限购令”的人数为X，则， 则X的可能取值为0,1,2，
那么， ， ，
所以X的分布列为：
则.
（3）由题意得：因为，， .
典例3、答案：（1）0.4； （2）分布列见解析，1.2； （3）186元，理由见解析.
解：（1）由频率分布直方图知，该连锁店的骑手的人均日快递业务量不少于65单的频率为：，
所以，随机选取一天，估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率为0.4.
（2）的可能值为0，1，2，3，依题意，，，
， ，
， ，
所以的分布列为：
期望.
（3）由频率分布直方图知，骑手每天送单的平均数为：，
因骑手每送1单可以提成3元，则骑手每天的收入的期望为（元）.
随堂练习：答案：（1）男生红绿色盲的发病率为，女生红绿色盲的发病率
（2）的分布列见解析，数学期望为 （3）
解：（1）设该校男生红绿色盲为事件，女生红绿色盲为事件， 则
（2）由表中的数据可知，已调查的学生中，有5人患红绿色盲，其中男生4人，女生1人，
所以可能取1，2，
则, ,
所以的分布列为
所以
（3）由题意得，
， 所以
典例4、答案：（1）表格见解析 （2） （2）答案见解析
解：（2）取事件A为“选取的2人中有人喜欢饮茶”，则，
取事件B为“选取的2人中有学生”，则事件AB为“选取的2人中即有人喜欢饮茶，又包含有学生”，
∴∴．
依题意，，
∴此次调研的结论为：有90%的把握认为家长相比于学生更喜欢饮茶．
随堂练习：答案： （1）①，②；
（2），有99.9%的把握认为口罩质量与感染新冠肺炎病毒的风险有关．
解：（1）①批次Ⅰ成品口罩的次品率为：．
②设批次Ⅰ的成品口罩红外线自动检测合格为事件，人工抽检合格为事件，
由已知，得，，
则工人在流水线进行人工抽检时，抽检一个口罩恰为合格品为事件，
．
（2）100个成品口罩中恰有1个不合格品的概率．
因此．
令，得．
当时，；当时，． 所以的最大值点为．
由（1）可知，，，故批次口罩的次品率低于批次Ⅰ，
故批次的口罩质量优于批次Ⅰ．
由条形图可建立列联表如下： 单位：人
．
因此，有99.9%的把握认为口罩质量与感染新冠肺炎病毒的风险有关．
典例5、答案： （1）；（2）表格见解析，能.
解: （1）设从这100名被检测者中，随机抽取一名不带菌者，检测结果呈阳性为事件，
根据统计图可知在不带菌者中，检测结果呈阳性的有5人， ∴.
（2）可作出列联表如下：
进一步计算得的观测值
所以，能够在犯错误概率不超过0.001的前提下认为“带菌”与“检测结果呈阳性有关.
随堂练习：答案： (1)； (2)；(3)列联表见解析，没有99%的把握认为对这两部历史战争题材影片的选择与性别有关.
解:(1)由图1知，“观看电影《八佰》的观众年龄低于30岁”的频率为，
由此估计事件C的概率为；
(2) 由图2知，参与调查的电影《金刚川》的100名购票观众中男性有61人，
从100名观众中依次抽两名，在第一次抽到男性的条件下，第二次仍抽到男性的事件B，
相当于从含60名男性观众的99名观众中任抽1人，抽到男性的事件，其概率为，
(3)观察图2得列联表如下：
则的观测值为，
由独立性检验知，没有99%的把握认为对这两部历史战争题材影片的选择与性别有关.
典例6、 （1）能在犯错误的概率不超过0.025的前提下认为喜欢盲拧与性别有关；（2）.
解:（1）
由表中数据可得，
故能在犯错误的概率不超过0.025的前提下认为喜欢盲拧与性别有关.
（2）6名男生中任意抽取2人共：15种结果.
2人成功完成时间恰好在同一组内分为两种情形：完成时间都在或都在
完成时间都在共有6种结果，完成时间都在有1种结果，
2人成功完成时间恰好在同一组内的概率为：.
随堂练习：答案： （1）， （2）
（3）填表见解析；没有以上的把握认为“频繁更换手机与性别有关”
解: （1）由题知男性顾客共有人， 女性顾客共有人，
按分层抽样抽取105人，则应该抽取男性顾客人，
女性顾客人； 所以，；
（2）记“随机从已抽取的105名且更换手机时间间隔为3至6个月（含3个月和6个月）的顾客中，抽取2人”为事件A，设男性分别为a，b，c，d，女性分别为e，f，
则事件A共包含，，，， ，，，
，， ，，15个可能结果，
其中2人均男性有，， ，，6种可能结果，
所以2人均是男性的概率为；
（3）由频率分布表可知，在抽取的105人中，男性顾客中频繁更换手机的有21人，女性顾客中频繁更换手机的有9人，据此可得列联表：
所以；因为
所以没有以上的把握认为“频繁更换手机与性别有关”.
年龄/岁
80岁以上
使用过打车软件人数
41
20
11
5
1
未使用过打车软件人数
1
3
9
6
3
成绩
男生（人数）
2
5
8
9
1
女生（人数）
a
b
10
3
2
男职工
女职工
使用
不使用
使用
不使用
款APP
72人
48人
40人
80人
款APP
60人
60人
84人
36人
月收入(单位：百元)
调查人数
500
1000
1500
1000
500
500
赞成人数
400
800
1200
414
99
87
人数
男生
高度近视
红绿色盲
3
√
×
√
2
√
√
×
1
√
√
√
1
×
×
√
2
×
√
×
喜欢饮茶
不喜欢饮茶
合计
家长
60
120
学生
50
合计
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
0.050
0.010
0.005
0.001
3.841
6.635
7.879
10.828
检测结果呈阳性
检测结果呈阴性
合计
不带菌者
带菌者
合计
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
影片
女性观众
男性观众
总计
《八佰》
100
《金刚川》
100
总计
86
114
200
0.1
0.05
0.01
0.001
2.706
3.841
6.635
10.828
喜欢盲拧
不喜欢盲拧
总计
男
23
30
女
11
总计
50
成功完成时间（分钟）

人数
10
4
4
2

0.10
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
事件间隔（月）
男性
x
8
9
18
12
8
4
女性
y
2
5
13
11
7
2
频繁更换手机
未频繁更换手机
合计
男性顾客
女性顾客
合计
P（）
0.100
0.050
0.010
0.001
2.706
3.841
6.635
10.828
X
0
1
2
P
0
1
2
3
0
1
2
X
0
1
2
P
0
1
2
3
0.216
0.432
0.288
0.064
1
2
喜欢饮茶
不喜欢饮茶
合计
家长
60
60
120
学生
30
50
80
合计
90
110
200
核酸检测结果
口罩批次
合计
呈阳性
12
3
15
呈阴性
28
57
85
合计
40
60
100
检测结果呈阳性
检测结果呈阴性
合计
不带菌者
5
45
50
带菌者
35
15
50
合计
40
60
100
影片
女性观众
男性观众
总计
《八佰》
47
53
100
《金刚川》
39
61
100
总计
86
114
200
喜欢盲拧
不喜欢盲拧
总计
男
23
7
30
女
9
11
20
总计
32
18
50
频繁更换手机
未频繁更换手机
合计
男性顾客
21
42
63
女性顾客
9
33
42
合计
30
75
105