人教A版 (2019)必修 第一册3.2 函数的基本性质备课课件ppt

这是一份人教A版 (2019)必修 第一册3.2 函数的基本性质备课课件ppt，共25页。PPT课件主要包含了符号表达，偶函数，奇函数，称yx为奇函数，练一练，答案t1，数形结合，分类讨论，转化与化归，课堂小结等内容，欢迎下载使用。
3.2.3 函数的奇偶性
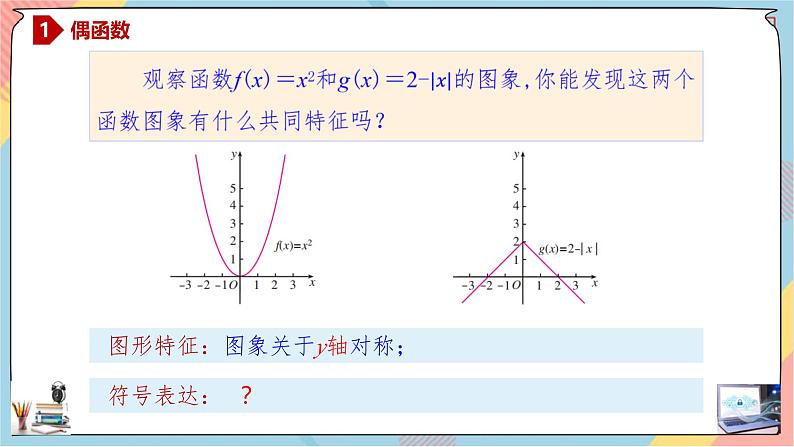
图形特征：图象关于y轴对称；
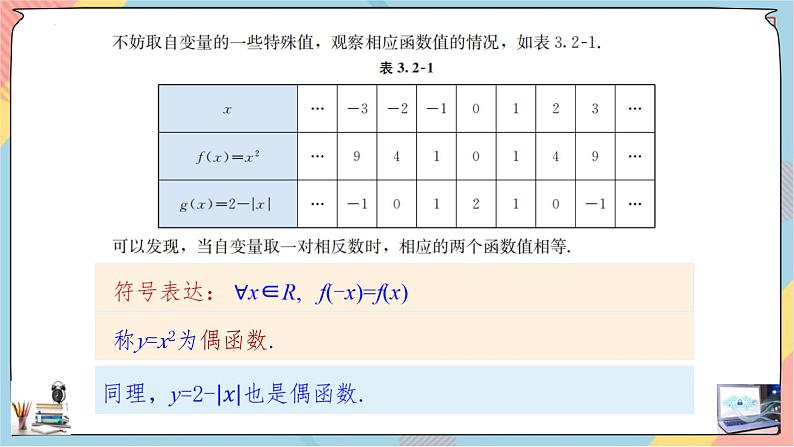
称y=x2为偶函数.
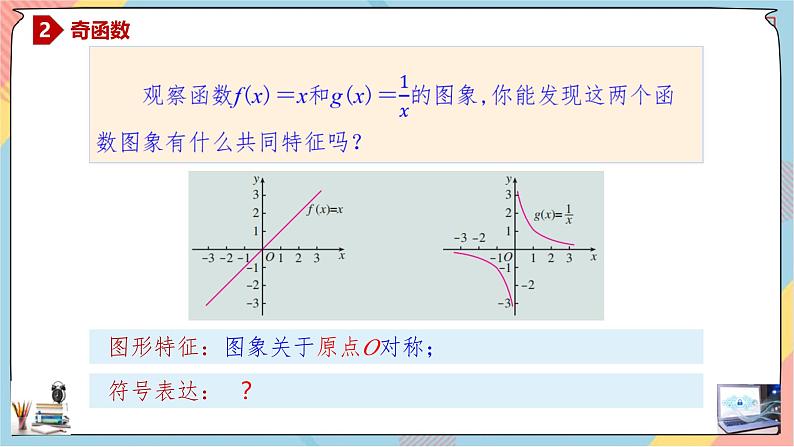
图形特征：图象关于原点O对称；
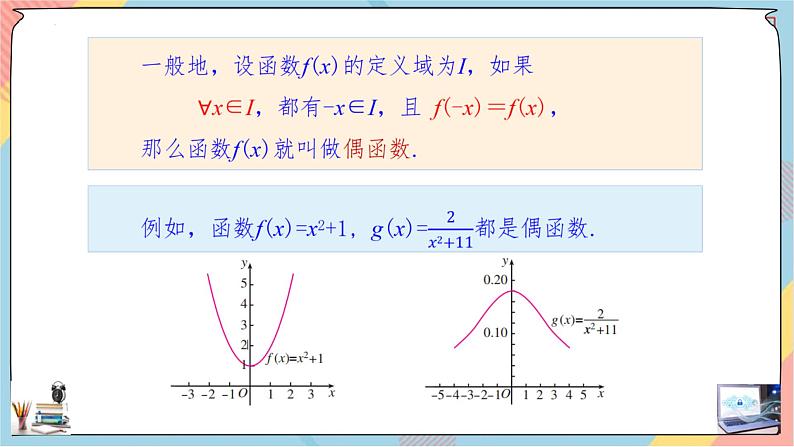
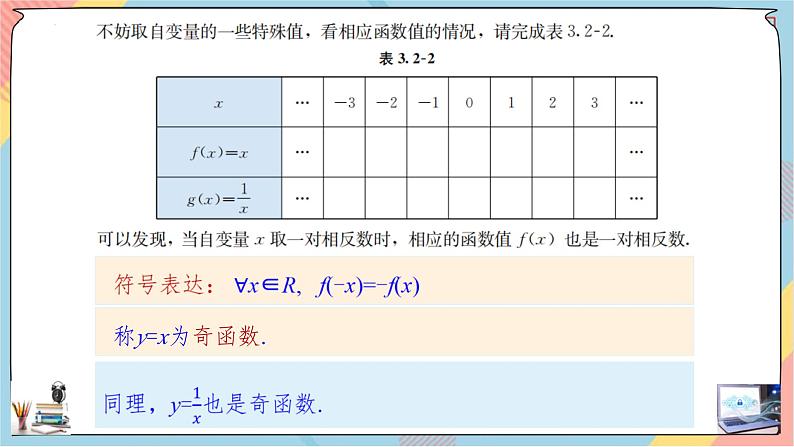
例如，函数 f(x)=x3就是奇函数.
1.奇函数f(x)的定义域是(2t-3, t)，则t= .
2.判断下列函数的奇偶性：
答案：(1) 偶 ; (2) 奇 ; (3) 奇 ; (4) 偶 ; (5) 非奇非偶 ; (6) 非奇非偶 ;
1.已知f(x)=ax3-bx+4(a,b∈R), f(m)=5, 则 f(-m)= .
解：令g(x)=ax2-bx，易知 g(-x)=-g(x) 又 g(m)= f(m)-4=1, 从而g(-m)=-g(m)=-1 故 f(-m)=g(-m)+4= 3
方法：利用奇函数的性质，推导出f(m)与f(-m)的关系.
2.设 f(x)是偶函数，g(x)是奇函数，且 f(x)+g(x)=x2+2x，求函数f(x)、g(x)的解析式.
解：用-x替换f(x) +g(x)=x2+2x中的x，得 f(-x)+g(-x)=x2-2x ① 由已知，f(-x)=f(x), g(-x)=-g(x)， 所以有： f(x)-g(x)=x2-2x ② 联立①②，解得f(x)=x2 ，g(x)=2x
方法：利用奇偶性质构造对偶式，是解决此类问题的关键.
3.函数f(x)是R上的奇函数，当x>0时，f(x)=x(1+x)+1； 求f(x)的解析式.
4.已知f(x)，g(x)是R上的奇函数，试判断 y=f(x)+g(x), y=f(x)g(x), y=f[g(x)]的奇偶性.
解：因为f(-x)+g(-x)=-(f(x)+g(x)) 所以y=f(x)+g(x)是R上的奇函数； 因为f(-x)g(-x)=(-f(x))(-g(x))=f(x)g(x) 所以y=f(x)g(x)是R上的偶函数； 因为f[g(-x)]=f[-g(x)]=-f[g(x)] 所以y=f[g(x)]是R上的奇函数.
方法：判断组合函数或复合函数的奇偶性时，先验证定义 域关于原点对称，再验证f(x)与f(-x) 的关系.
5.定义在［-5,5]上的奇函数f(x)部分图象如图， 则不等式 x f(x)>0 的解集为 .
方法：奇函数图象关于坐标原点对称；数与形结合，可直接 读取不等式的解集.
答案：(-5，-2)∪(0，2)
解：(1)当x1, 所以 f(-x)=(-x-5)2-4=(x+5)2-4=f(x) 当x>1时，-x0 的解集为 .
简解：由 f(x-1)+f(2x+4)>0 推出 f(x-1)>-f(2x+4)= f(-2x-4) 又f(x)在[0,+∞)上单调递减， 由对称性知 f(x)在R上单调递减, 所以x-1