浙教版八年级数学上册专项素养综合练(三)分类讨论思想在等腰三角形中的四种应用课件

这是一份浙教版八年级数学上册专项素养综合练(三)分类讨论思想在等腰三角形中的四种应用课件，共22页。

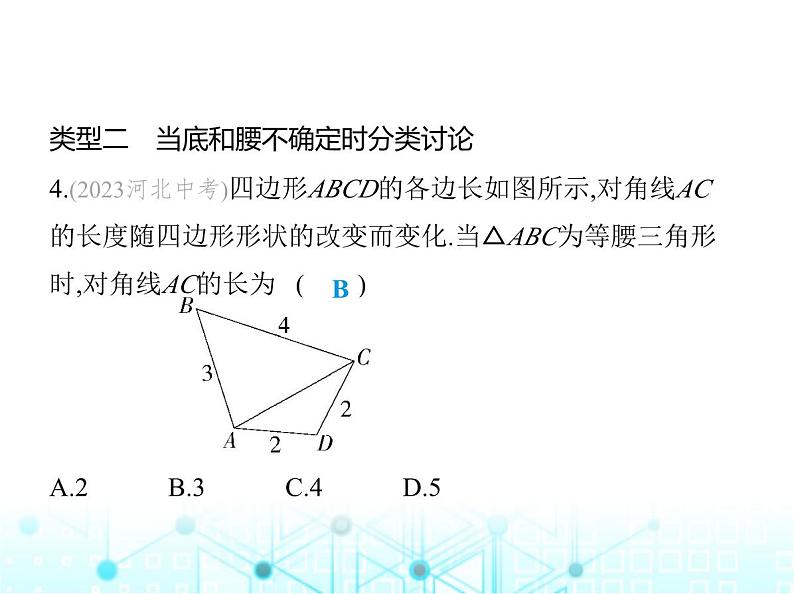
专项素养综合练(三)分类讨论思想在等腰三角形中的四种应用类型一　当顶角或底角不确定时分类讨论1.(2023浙江嘉兴桐乡一模改编)若等腰△ABC的一个外角等于110°,则该三角形的顶角度数为 (　　)A.40°　　     B.70°C.55°或70°　　    D.40°或70°D解析    ∵等腰△ABC的一个外角为110°,∴△ABC的一个内角为180°-110°=70°.分两种情况讨论:(1)当70°的内角为等腰三角形顶角时,顶角度数为70°;(2)当70°的内角为等腰三角形的底角时,顶角度数为180°-70°×2=40°.∴顶角为40°或70°.故选D.2.(2023陕西宝鸡一模改编)已知等腰△ABC中,∠A=20°,则∠B的度数为 (　　)A.20°　　     B.140°C.20°或140°　　    D.20°或80°或140°D3.(2024浙江绍兴诸暨浣江教育集团期中)若一个等腰三角形的一个内角是另一个内角的一半,则此三角形的底角度数为　　 　    .72°或45°解析　分两种情况:当等腰三角形的顶角是底角的一半时,设等腰三角形的顶角为x,则底角为2x,由题意得x+2x+2x=180°,解得x=36°,∴等腰三角形的底角为72°;当等腰三角形的底角是顶角的一半时,设等腰三角形的底角为y,则顶角为2y,由题意得y+y+2y=180°,解得y=45°,∴等腰三角形的底角为45°.综上所述,此三角形底角度数为72°或45°,故答案为72°或45°.类型二　当底和腰不确定时分类讨论4.(2023河北中考)四边形ABCD的各边长如图所示,对角线AC的长度随四边形形状的改变而变化.当△ABC为等腰三角形时,对角线AC的长为 (　　) A.2　　    B.3　　    C.4　　    D.5B解析    ∵△ABC为等腰三角形,∴AB=AC或AC=BC,当AC=BC=4时,AD+CD=AC=4,此时不能组成三角形;当AC=AB=3时,AD+CD=4>3,能组成三角形,∴AC=3.故选B.5.(2024天津九十二中月考改编)已知等腰三角形的两边长分别是m,n,若m,n满足|m-4|+(n-6)2=0,则它的周长是 (　　)A.14　　    B.16　　    C.14或16　　    D.14或18C解析    ∵|m-4|+(n-6)2=0,∴m-4=0,n-6=0,解得m=4,n=6,∵4+4>6,∴以4,4,6为三边长可以组成三角形,三角形周长为4+4+6=14,∵4+6>6,∴以4,6,6为三边长可以组成三角形,三角形周长为4+6+6=16.故选C.6.(2024天津滨海塘沽一中期中)如图,在4×4的正方形网格中有两个格点A、B,连结AB,在网格中再找一个格点C,使得△ABC是等腰三角形,满足条件的格点C的个数是 (　　) A.5　　    B.6　　    C.8 　　    D.9C解析    如图: 分三种情况:当BA=BC时,以点B为圆心,BA长为半径作圆,点C1,C2,C3即为所求;当AB=AC时,以点A为圆心,AB长为半径作圆,点C4,C5,C6,C7,C8即为所求;当CA=CB时,作AB的垂直平分线,与正方形网格的交点不在格点上.综上所述,满足条件的格点C的个数是8.故选C.类型三　 当高的位置不确定时分类讨论7.(2024江苏宿迁泗洪期中)数学教师在黑板上呈现一道试题:“已知AD是等腰三角形ABC的腰BC上的高,且∠DAB=60°.请画出符合条件的图形,并求出△ABC各角的度数.”小明同学画出如下图形,并在图中标出△ABC 各角的度数.请你画出所有符合条件且不同于小明同学的图形,并标出△ABC各角的度数.解析　①如图1,当点B为顶角的顶点,且AD在三角形内部时,∠B=90°-∠DAB=90°-60°=30°,∠BAC=∠C=75°;②如图2,当点B为顶角的顶点,且AD在三角形外部时,∠ABC=∠D+∠DAB=90°+60°=150°,∠BAC=∠C=15°. 类型四　当腰的垂直平分线不确定时分类讨论8.(2024广西河池宜州期中)在△ABC中,AB=AC,AB的垂直平分线与AC所在直线的夹角(锐角)为50°,则这个等腰三角形的顶角度数为 (　　)A.40°　　     B.50°C.40°或140°　　    D.50°或130°C解析    分两种情况讨论:①当△ABC是锐角三角形时,如图1,∵DE是AB的垂直平分线,∴DE⊥AB,∴∠ADE=90°,∵∠AED=50°,∴∠A=90°-∠AED=40°;②当△ABC是钝角三角形时,如图2,∵DE是AB的垂直平分线,∴DE⊥AB,∴∠ADE=90°,∵∠AED=50°,∴∠DAE=90°-∠AED=40°,∴∠DAC=180°-∠DAE=140°.综上所述,这个等腰三角形的顶角度数为40°或140°.故选C.9.如图所示,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC或BC的延长线于点M.(1)如图1所示,若∠A=40°,求∠NMB的大小.(2)如图2所示,如果将(1)中的∠A的度数改为70°,其余条件不变,再求∠NMB的大小.(3)你发现了什么规律?写出猜想,并说明理由.解析　(1)∵AB=AC,∠A=40°,∴∠ABC=∠ACB= (180°-∠A)=70°,∵MN是AB的垂直平分线,∴∠MNB=90°,∴∠NMB=90°-∠B=20°.(2)∵AB=AC,∠A=70°,∴∠B=∠ACB= (180°-∠A)=55°,∵MN是AB的垂直平分线,∴∠MNB=90°,∴∠NMB=90°-∠B=35°.(3)∠NMB= ∠A.理由:∵AB=AC,∴∠B=∠ACB= (180°-∠A)=90°- ∠A,∵MN是AB的垂直平分线,∴∠MNB=90°,∴∠NMB=90°-∠B=90°- = ∠A.