初中数学人教版（2024）八年级上册12.2 三角形全等的判定学案设计

这是一份初中数学人教版（2024）八年级上册12.2 三角形全等的判定学案设计，共6页。

1.知道“边角边”条件的内容，会用“边角边”证明两个三角形全等.(重点)
2.通过做一做、画一画等过程探究、归纳两个三角形全等的条件：SAS.
3.在具体应用上，通过练习，感悟几何题的分析证明过程.
自主学习
学习任务一 回顾知识
1.怎样的两个三角形是全等三角形？
2.全等三角形的性质有哪些？
学习任务二 探究三角形全等的条件
1.组织学生做游戏(找朋友)，游戏规则：发放图1中的各类卡片若干张，利用全等三角形的概念找到与自己手中的三角形卡片全等的卡片，即为朋友.

图1
朋友的共同点是什么？
2.如图2①，已知△ABC，画△A′B′C′，使A′B′＝AB，A′C′＝AC，∠A′＝∠A.

① ②
图2
画法：(1)画∠DA′E＝∠A；
(2)在射线A′D上截取A′B′＝AB，在射线A′E上截取A′C′＝AC；
(3)连接B′C′.如图2②，△A′B′C′即为所求.
把画好的△A′B′C′剪下来放在△ABC上，观察这两个三角形是否全等.
SAS：
强调：
学习任务三 SAS的运用
如图3，有一池塘，要测池塘两端A，B之间的距离，可先在平地上取一个点C，从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D，使CD＝CA.连接BC并延长到点E，使CE＝CB，连接DE，那么量出DE的长就是A，B之间的距离.为什么？
图3
解：



合作探究
教材第39页思考.
我们知道，两边和它们的夹角对应相等的两个三角形全等.由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗？为什么？
如图4，把一长一短的两根细木棍的一端固定在一起，使长木棍的另一端与射线BC的端点B重合，固定住长木棍，转动短木棍，其另一端落在射线BC上的C点或D点，形成△OBC或△OBD.这个实验说明了什么？
图4
师生分析：图4中的△OBD和△OBC满足两边和其中一边的对角分别相等，即OB＝OB，OC＝OD，∠B＝∠B，但△OBD与△OBC不全等.
这说明：
已知：如图5，AB＝AC，AD＝AE，∠BAC＝∠DAE，求证：△ABD≌ △ACE.
图5
证明：

当堂达标
1.下列条件中，能使△ABC≌△DEF的条件是( )
A.AB＝DE，∠A＝∠D，BC＝EF
B.AB＝DF，∠B＝∠E，BC＝EF
C.AB＝EF，∠A＝∠D，AC＝DF
D.BC＝EF，∠C＝∠F，AC＝DF
2.如图6，点O是线段AB的中点，OD∥BC且OD＝BC.
(1)求证：△AOD≌△OBC.
(2)若∠ADO＝35°，求∠DOC的度数.
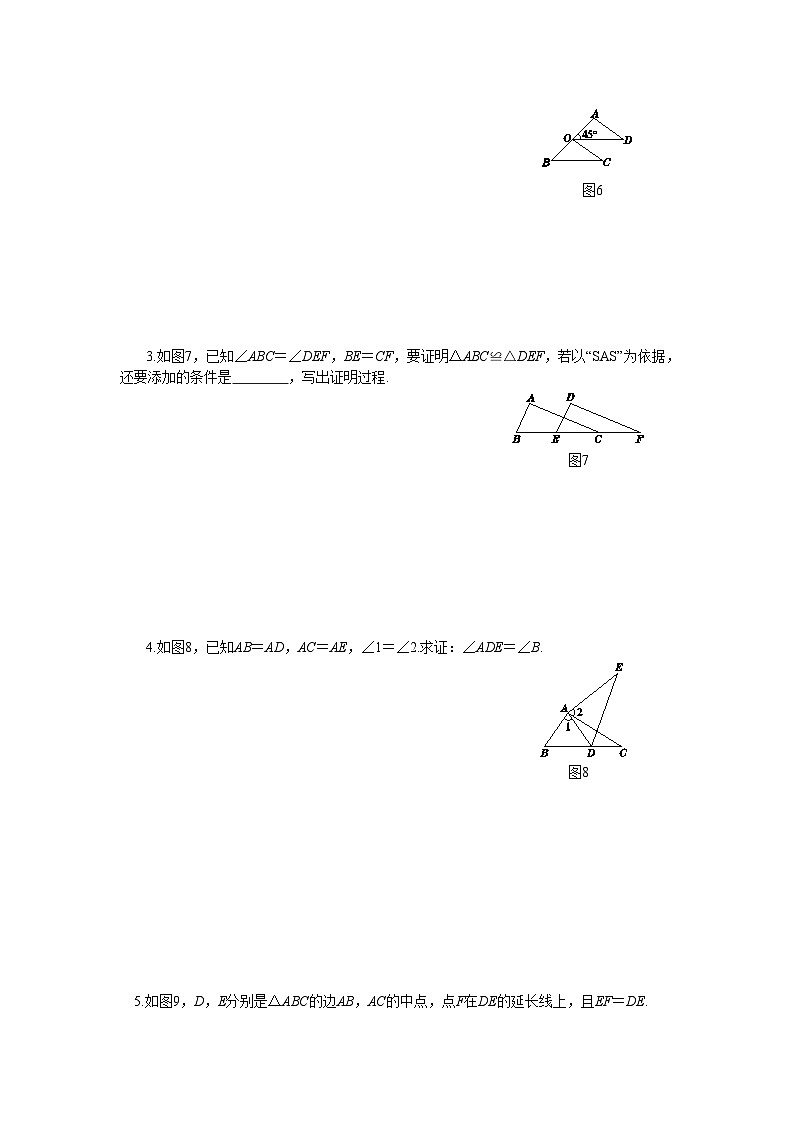
图6
3.如图7，已知∠ABC＝∠DEF，BE＝CF，要证明△ABC≌△DEF，若以“SAS”为依据，还要添加的条件是 ，写出证明过程.
图7
4.如图8，已知AB＝AD，AC＝AE，∠1＝∠2.求证：∠ADE＝∠B.
图8
5.如图9，D，E分别是△ABC的边AB，AC的中点，点F在DE的延长线上，且EF＝DE.
求证：(1)BD＝FC.
(2)AB∥CF.
图9
课后提升
两个大小不同的等腰直角三角尺如图10①所示放置，图10②是由它抽象出的几何图形，点B，C，E在同一条直线上，连接DC，AE与DC相交于点F.
(1)请找出图10②中的全等三角形，并给予证明(说明：结论中不得含有未标识的字母)；
(2)证明：DC⊥BE.
① ②
图10
反思感悟
我的收获：


我的易错点：


参考答案
当堂达标
1.D
2.(1)证明：∵ 点O是线段AB的中点，∴ AO＝BO.
∵ OD∥BC，∴ ∠AOD＝∠OBC，
在△AOD和△OBC中，∴ △AOD≌△OBC(SAS).
(2)解：∵ △AOD≌△OBC，∴ ∠ADO＝∠OCB＝35°.
∵ OD∥BC，∴ ∠DOC＝∠OCB＝35°.
3.解：AB＝DE.
证明：∵ BE＝CF，∴ BE+EC＝CF+EC，∴ BC＝EF.
在△ABC和△DEF中，∴ △ABC≌△DEF(SAS).
4.证明：∵ ∠1＝∠2，∴ ∠1+∠DAC＝∠2+∠DAC，∴ ∠BAC＝∠DAE.
在△ABC和△ADE中，
∴ △ABC≌△ADE(SAS)，∴ ∠ADE＝∠B.
5.证明：(1)∵ E是AC的中点，∴ AE＝CE.
在△ADE和△CFE中，
∴ △ADE≌△CFE(SAS).∴ AD＝CF.
∵ D为AB的中点，∴ AD＝BD.∴ BD＝FC.
(2)由(1)知△ADE≌△CFE，∴ ∠A＝∠ECF，∴ AB∥CF.
课后提升
(1)解：△ABE≌△ACD.
∵ △ABC和△ADE是等腰直角三角形，
∴ AB＝AC，AE＝AD，∠BAC＝∠EAD＝90°.
∴ ∠BAC+∠EAC＝∠DAE+∠EAC.∴ ∠BAE＝∠CAD.
在△ABE和△ACD中，∴ △ABE≌△ACD(SAS).
(2)证明：∵ △ABE≌△ACD，∴ ∠AEB＝∠ADC.
∵ ∠ADC+∠AFD＝90°，∴ ∠AEB+∠AFD＝90°.
∵ ∠AFD＝∠CFE，∴ ∠AEB+∠CFE＝90°，
∴ ∠FCE＝90°，∴ DC⊥BE.