






必修 第二册6.1 平面向量的概念课文配套课件ppt
展开自主预习·新知导学
一、向量的概念【问题思考】1.在物理中,位移与距离是同一个概念吗?现实世界中有各种各样的量,如年龄、身高、体重、力、速度、面积、体积、温度等,怎样正确区分这些量呢?提示:在物理中,位移与距离不是同一个概念;这些量中有些只有大小,没有方向,但有些既有大小又有方向,因此应该从大小和方向两个方面对这些量进行区分.
2.填空:(1)向量:在数学中,我们把既有大小又有方向的量叫做向量.(2)数量:把只有大小没有方向的量称为数量.
二、有向线段【问题思考】1.在物理中,我们经常用“带有方向的线段”来表示位移,那么线段与带有方向的线段相同吗?提示:线段与带有方向的线段是不同的,线段只有长度,带有方向的线段不但有长度,还有方向、起点等.
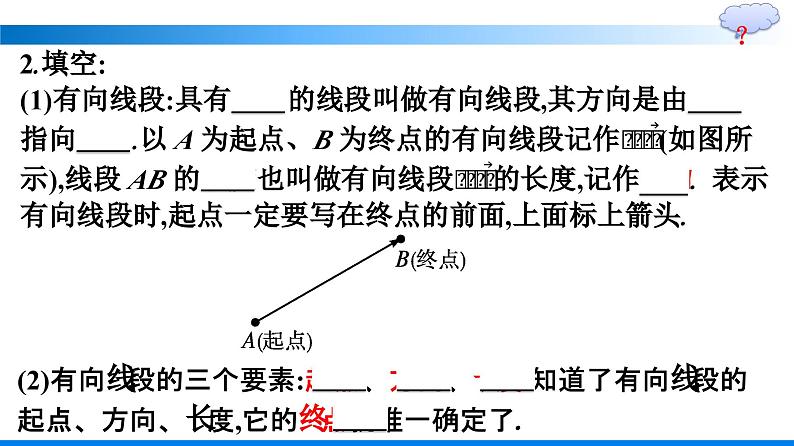
(2)有向线段的三个要素:起点、方向、长度.知道了有向线段的起点、方向、长度,它的终点就唯一确定了.
三、向量的几何表示【问题思考】1.对于一个实数,可以用数轴上的点表示;对于一个二次函数,可以用一条抛物线表示……数学中有许多量都可以用几何方式表示,你认为如何用几何方式表示向量最合适?提示:由于向量既有大小又有方向,因此可用有向线段来表示.
四、两个特殊向量【问题思考】1.零向量的方向是什么?两个单位向量的方向相同吗?提示:零向量的方向是任意的.两个单位向量的方向不一定相同.2.
3.做一做:下列说法正确的是( )A.向量的模是一个正实数B.零向量没有方向C.单位向量的模等于1个单位长度D.零向量就是实数0解析:向量的模是一个非负实数,零向量的方向是任意的,零向量不是实数0,故A,B,D均错,只有C正确.答案:C
五、 向量的关系【问题思考】1.向量由其模和方向所确定.对于两个向量a,b,就其模相等与不相等,方向相同与不相同而言,可能的情形有哪几种?提示:有四种情形:模相等,方向相同;模相等,方向不相同;模不相等,方向相同;模不相等,方向不相同.2.如果两个向量所在的直线互相平行,那么这两个向量的方向有什么关系?提示:方向相同或相反.
4.做一做:下列说法正确的是( )
B.与实数类似,对于两个向量a,b,有a=b,a>b,a
合作探究·释疑解惑
探究一 向量的有关概念
分析:明确向量的有关概念,根据定义进行判定.
解析:|a|=|b|仅说明a与b的模相等,但不能说明它们方向的关系,故A错误.
【变式训练1】 下列说法正确的是( )A.数量可以比较大小,向量也可以比较大小B.向量的模可以比较大小C.模为1的向量都是相等向量D.由于零向量的方向不确定,因此零向量不能与任意向量平行解析:向量不能比较大小,故A不正确;向量的模是一个数量,可以比较大小,故B正确;相等向量不但模相等,方向也相同,故C不正确;规定零向量与任意向量平行,故D不正确.答案:B
【例2】 如图所示,在坐标纸上(每个小方格的边长均为1),用直尺和圆规作出下列向量:
分析:先确定起点,再根据大小和方向确定出终点,即可作出向量.
1.准确作出向量的方法是先确定向量的起点,再确定向量的方向,最后根据向量的大小确定向量的终点.2.注意事项:在书写有向线段时,要注意起点和终点的不同;在书写字母表示时,不要忘了字母上的箭头.
探究三 相等向量与共线向量
相等向量与共线向量的探求方法:(1)寻找相等向量:先找与表示已知向量的有向线段长度相等的向量,再确定哪些是同向共线.(2)寻找共线向量:先找与表示已知向量的有向线段平行或共线的线段,再构造同向与反向的向量,注意不要漏掉以表示已知向量的有向线段的终点为起点,起点为终点的向量.提醒:与向量平行相关的问题中,不要忽视零向量.
提示:由于对零向量、单位向量、相等向量、平行向量等概念理解不清,混淆它们之间的区别与联系导致错选.
明确向量及其相关概念的联系与区别:(1)区分向量与数量.向量既强调大小,又强调方向,而数量只与大小有关.(2)明确向量与有向线段的区别.有向线段有三要素:起点、方向、长度,只要起点不同,另外两个要素相同也不是同一条有向线段,但决定向量的要素只有两个:大小和方向,与表示向量的有向线段的起点无关.(3)零向量和单位向量都是通过模的大小来确定的,零向量的方向是任意的.
(4)平行向量也叫共线向量,当两共线向量的方向相同且模相等时,两向量为相等向量.
1.下列各量是向量的是( )A.时间B.速度C.面积D.长度解析:速度既有大小又有方向,是向量,其余均是数量.答案:B
3.在同一平面内,如果把平行于某一非零向量的一切向量的起点放在同一点,那么这些向量的终点所构成的图形是( )A.一条线段B.一条直线C.圆上一群孤立的点D.一个半径为1的圆解析:因为向量的起点确定,且向量平行于同一非零向量,所以随向量模的变化,向量的终点构成一条直线.答案:B
高中数学人教A版 (2019)必修 第二册第六章 平面向量及其应用6.1 平面向量的概念教学课件ppt: 这是一份高中数学人教A版 (2019)必修 第二册<a href="/sx/tb_c4000290_t3/?tag_id=26" target="_blank">第六章 平面向量及其应用6.1 平面向量的概念教学课件ppt</a>,共23页。PPT课件主要包含了学科素养,不能方向错误,力是如何表示的,手书写向量时要带箭头,相同或相反,长度相等方向相同,a∥b,a∥c等内容,欢迎下载使用。
数学必修 第二册第六章 平面向量及其应用6.1 平面向量的概念教学ppt课件: 这是一份数学必修 第二册<a href="/sx/tb_c4000290_t3/?tag_id=26" target="_blank">第六章 平面向量及其应用6.1 平面向量的概念教学ppt课件</a>,共59页。PPT课件主要包含了知识梳理,题型探究,随堂演练,课时对点练等内容,欢迎下载使用。
高中人教A版 (2019)第六章 平面向量及其应用6.1 平面向量的概念授课课件ppt: 这是一份高中人教A版 (2019)第六章 平面向量及其应用6.1 平面向量的概念授课课件ppt,共21页。PPT课件主要包含了学习目标,谁更重,猫能捉住老鼠吗,探索新知,向量的定义,课堂练习,课堂小结,课后作业等内容,欢迎下载使用。













