2024年中考数学二轮复习 二次函数压轴题 专项提升练习七（含答案）

这是一份2024年中考数学二轮复习 二次函数压轴题 专项提升练习七（含答案），共15页。
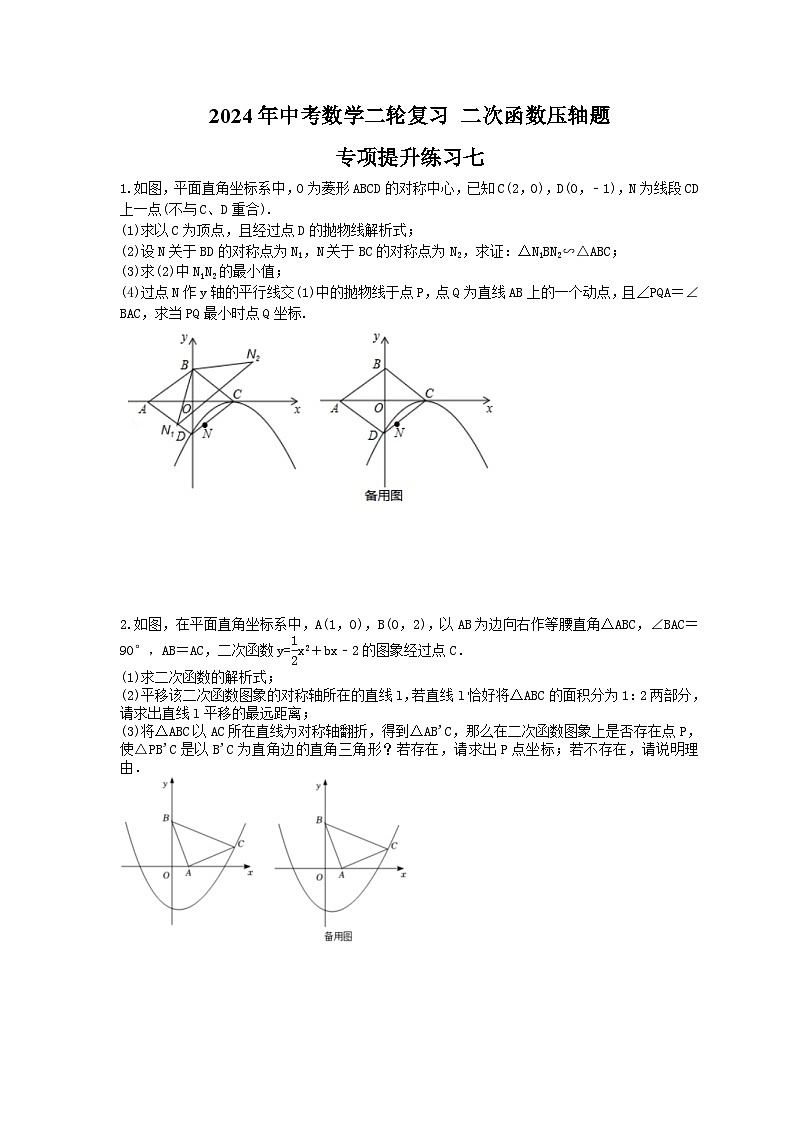
如图，平面直角坐标系中，O为菱形ABCD的对称中心，已知C(2，0)，D(0，﹣1)，N为线段CD上一点(不与C、D重合).
(1)求以C为顶点，且经过点D的抛物线解析式；
(2)设N关于BD的对称点为N1，N关于BC的对称点为N2，求证：△N1BN2∽△ABC；
(3)求(2)中N1N2的最小值；
(4)过点N作y轴的平行线交(1)中的抛物线于点P，点Q为直线AB上的一个动点，且∠PQA＝∠BAC，求当PQ最小时点Q坐标.
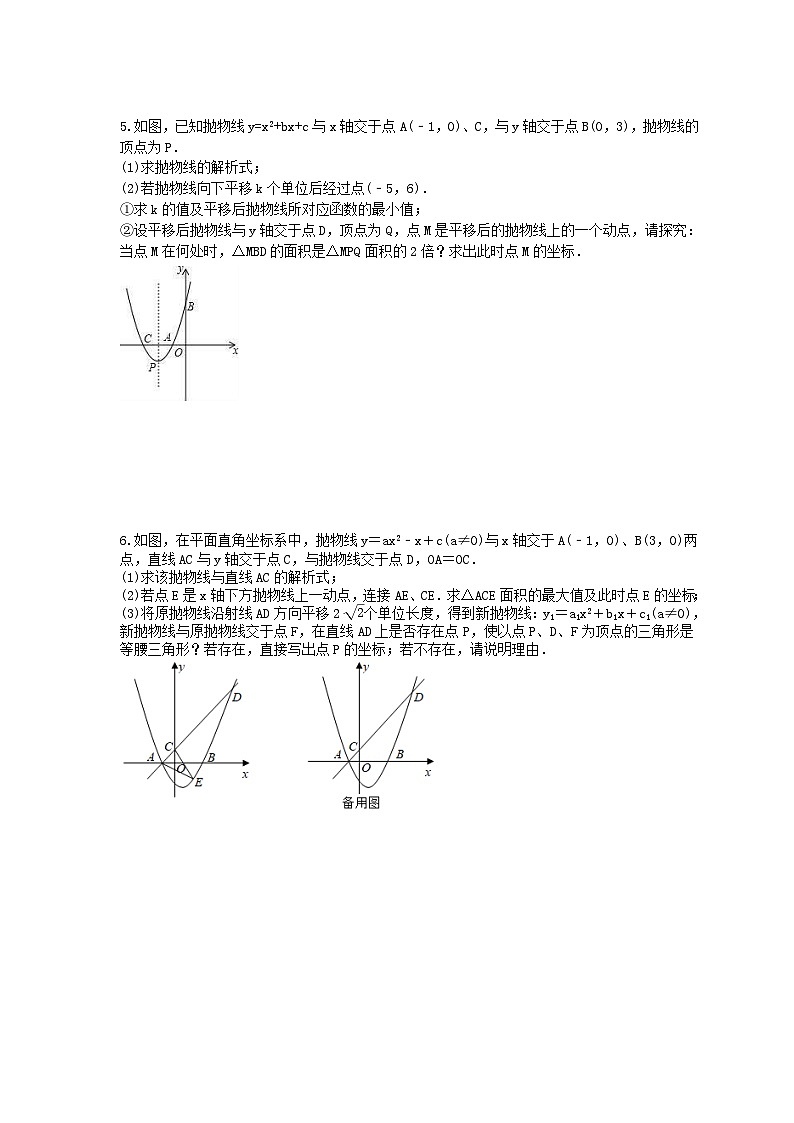
如图，在平面直角坐标系中，A(1，0)，B(0，2)，以AB为边向右作等腰直角△ABC，∠BAC＝90°，AB＝AC，二次函数y=eq \f(1,2)x2＋bx﹣2的图象经过点C．
(1)求二次函数的解析式；
(2)平移该二次函数图象的对称轴所在的直线l，若直线l恰好将△ABC的面积分为1：2两部分，请求出直线l平移的最远距离；
(3)将△ABC以AC所在直线为对称轴翻折，得到△AB'C，那么在二次函数图象上是否存在点P，使△PB'C是以B'C为直角边的直角三角形？若存在，请求出P点坐标；若不存在，请说明理由．
如图，抛物线y=﹣x2+bx+c和直线y=x+1交于A，B两点，点A在x轴上，点B在直线x=3上，直线x=3与x轴交于点C.
(1)求抛物线的解析式；
(2)点P从点A出发，以每秒eq \r(2)个单位长度的速度沿线段AB向点B运动，点Q从点C出发，以每秒2个单位长度的速度沿线段CA向点A运动，点P，Q同时出发，当其中一点到达终点时，另一个点也随之停止运动，设运动时间为t秒(t＞0).以PQ为边作矩形PQNM，使点N在直线x=3上.
①当t为何值时，矩形PQNM的面积最小？并求出最小面积；
②直接写出当t为何值时，恰好有矩形PQNM的顶点落在抛物线上.
如图，在平面直角坐标系中，抛物线y=- eq \f(1,2)x2+eq \f(3,2)x+2与x轴相交于点A、B，交y轴于点C，抛物线的对称轴交x轴于点N，交线段AC于点M.点F是线段MA上的动点，连接NF，过点N作NG⊥NF交△ABC的边于点G.
(1)求证：△ABC是直角三角形；
(2)当点G在边BC上时，连接GF，∠NGF的度数变化吗？若变化，请说明理由；若不变，请求出∠NGF的正切值；
(3)设点F的横坐标为n，点G的纵坐标为m，在整个运动过程中，直接写出m与n的函数关系式，并注明自变量n的取值范围.
如图，已知抛物线y=x2+bx+c与x轴交于点A(﹣1，0)、C，与y轴交于点B(0，3)，抛物线的顶点为P．
(1)求抛物线的解析式；
(2)若抛物线向下平移k个单位后经过点(﹣5，6)．
①求k的值及平移后抛物线所对应函数的最小值；
②设平移后抛物线与y轴交于点D，顶点为Q，点M是平移后的抛物线上的一个动点，请探究：
当点M在何处时，△MBD的面积是△MPQ面积的2倍？求出此时点M的坐标．
如图，在平面直角坐标系中，抛物线y＝ax2﹣x＋c(a≠0)与x轴交于A(﹣1，0)、B(3，0)两点，直线AC与y轴交于点C，与抛物线交于点D，OA＝OC．
(1)求该抛物线与直线AC的解析式；
(2)若点E是x轴下方抛物线上一动点，连接AE、CE．求△ACE面积的最大值及此时点E的坐标；
(3)将原抛物线沿射线AD方向平移2eq \r(2)个单位长度，得到新抛物线：y1＝a1x2＋b1x＋c1(a≠0)，新抛物线与原抛物线交于点F，在直线AD上是否存在点P，使以点P、D、F为顶点的三角形是等腰三角形？若存在，直接写出点P的坐标；若不存在，请说明理由．
如图，已知抛物线y=ax2＋bx＋c(a≠0)与x轴交于点A(1，0)和点B(﹣3，0)，与y轴交于点C，且OC=OB．
(1)求此抛物线的解析式；
(2)若点E为第二象限抛物线上一动点，连接BE，CE，求四边形BOCE面积的最大值，并求出此时点E的坐标；
(3)点P在抛物线的对称轴上，若线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，求点P的坐标．
如图，已知抛物线y＝a(x﹣3)(x＋6)过点A(﹣1，5)和点B(﹣5，m)，与x轴的正半轴交于点C．
(1)求a，m的值和点C的坐标；
(2)若点P是x轴上的点，连接PB，PA，当＝时，求点P的坐标；
(3)在抛物线上是否存在点M，使A，B两点到直线MC的距离相等？若存在，求出满足条件的点M的横坐标；若不存在，请说明理由．
\s 0 答案
解：(1)由已知，设抛物线解析式为y＝a(x﹣2)2
把D(0，﹣1)代入，得a＝﹣eq \f(1,4)，∴y＝﹣eq \f(1,4)(x﹣2)2
(2)如图1，连结BN.
∵N1，N2是N的对称点
∴BN1＝BN2＝BN，∠N1BD＝∠NBD，∠NBC＝∠N2BC
∴∠N1BN2＝2∠DBC
∵四边形ABCD是菱形
∴AB＝BC，∠ABC＝2∠DBC
∴∠ABC＝∠N1BN2，
∴△ABC∽△N1BN2
(3)∵点N是CD上的动点，
∴点到直线的距离，垂线段最短，
∴当BN⊥CD时，BN最短.
∵C(2，0)，D(0，﹣1)
∴CD＝eq \r(5)，
∴BNmin＝＝eq \f(4\r(5),5)，
∴BN1min＝BNmin＝eq \f(4\r(5),5)，
∵△ABC∽△N1BN2
∴，N1N2min＝eq \f(16,5)，
(4)如图2，
过点P作PE⊥x轴，交AB于点E.
∵∠PQA＝∠BAC
∴PQ1∥AC
∵菱形ABCD中，C(2，0)，D(0，﹣1)
∴A(﹣2，0)，B(0，1)
∴lAB：y＝eq \f(1,2)x＋1
不妨设P(m，﹣eq \f(1,4)(m﹣2)2)，则E(m，eq \f(1,2)m＋1)
∴PE＝eq \f(1,4)m2﹣eq \f(1,2)m＋2
∴当m＝1时，，
∴Q(﹣eq \f(5,2)，﹣eq \f(1,4)).
此时，PQ1最小，最小值为＝eq \f(7,2)，
∴PQ1＝PQ2＝eq \f(7,2).
解：(1)过点C作CK⊥x轴交于点K，如图：
∵∠BAO＋∠CAK＝90°，∠BAO＋∠OBA＝90°，
∴∠CAK＝∠OBA，
又∠AOB＝∠AKC＝90°，AB＝AC，
∴△ABO≌△CAK(AAS)，
∴OB＝AK＝2，AO＝CK＝1，
∴OK＝AO＋AK＝1＋2＝3，
∴点C的坐标为(3，1)，
将点C的坐标代入y＝eq \f(1,2)x2＋bx﹣2得：1＝eq \f(1,2)×9＋3b﹣2，解得：b＝﹣eq \f(1,2)，
∴二次函数表达式为y＝eq \f(1,2)x2﹣eq \f(1,2)x﹣2；
(2)由y＝eq \f(1,2)x2﹣eq \f(1,2)x﹣2可知抛物线的对称轴为直线x＝eq \f(1,2)，且当直线l将△ABC的面积分为左部分比右部分＝2：1时，直线l平移的距离最远，如图：
设此时直线l分别交边BC、AC分别为点M、N，
由B(0，2)，C(3，1)可得直线BC解析式为y＝﹣eq \f(1,3)x＋2，
由A(1，0)，C(3，1)可得直线AC解析式为y＝eq \f(1,2)x﹣eq \f(1,2)，
设点M的坐标为(t,﹣eq \f(1,3)t＋2)，点N坐标为(t,eq \f(1,2)t﹣eq \f(1,2))，1≤t＜3，
∵直线l将△ABC的面积分为左部分比右部分＝2：1，
∴S△CMN＝eq \f(1,3)S△ABC，
又AB＝eq \r(5)，
∴eq \f(1,2)×(3﹣t)(﹣eq \f(1,3)t＋2﹣eq \f(1,2)t＋eq \f(1,2))＝eq \f(1,3)×eq \f(1,2)×eq \r(5)×eq \r(5)，解得t=3﹣eq \r(2)或3＋eq \r(2)(舍去)，
∴直线l平移的距离最远是3﹣eq \r(2)﹣eq \f(1,2)＝eq \f(5,2)﹣eq \r(2)；
(3)在二次函数图象上存在点P，使△PB'C是以B'C为直角边的直角三角形，理由如下：
①当∠PCB'＝90°时，如图：
∵B，B'关于直线AC对称，
∴∠BCA＝∠B'CA＝45°，
∴∠BCB'＝90°，即点P为直线BC与抛物线的另外一个交点，
由得：或，
∴点P的坐标为；
②当∠CB'P＝90°时，过B'作BT⊥x轴于T，如图：
∵B，B'关于直线AC对称，∠BAC＝90°，
∴BA＝B'A，
∵∠BAO＝∠B'AT，∠BOA＝90°＝∠B'TA，
∴△BOA≌△B'TA(AAS)，
∴AT＝AO＝1，OB＝B'T＝2，
∴OT＝AO＋AT＝2，
∴B'(2，﹣2)，
由①知，∠BCB'＝90°，
∴过B'作BC的平行线，与抛物线的交点即为P，
∵直线BC解析式为y＝﹣eq \f(1,3)x＋2，B'(2，﹣2)，
∴B'P解析式为y＝﹣eq \f(1,3)x﹣eq \f(4,3)，
由得或，
∴点P的坐标为(﹣1，﹣1)或(eq \f(4,3),﹣eq \f(16,9))，
综上所述，点P的坐标为：或(﹣1，﹣1)或．
解：(1)由已知，B点横坐标为3
∵A、B在y=x+1上
∴A(﹣1，0)，B(3，4)
把A(﹣1，0)，B(3，4)代入y=﹣x2+bx+c得
解得
∴抛物线解析式为y=﹣x2+3x+4；
(2)①过点P作PE⊥x轴于点E
∵直线y=x+1与x轴夹角为45°，P点速度为每秒eq \r(2)个单位长度
∴t秒时点E坐标为(﹣1+t，0)，Q点坐标为(3﹣2t，0)
∴EQ=4﹣3t，PE=t
∵∠PQE+∠NQC=90°
∠PQE+∠EPQ=90°
∴∠EPQ=∠NQC
∴△PQE∽△QNC
∴
∴矩形PQNM的面积S=PQ•NQ=2PQ2
∵PQ2=PE2+EQ2
∴S=2()2=20t2﹣48t+32
当t=时，S最小=20×(eq \f(6,5))2﹣48×eq \f(6,5)+32=3.2
②由①点Q坐标为(3﹣2t，0)，P坐标为(﹣1+t，t)
∴△PQE∽△QNC，可得NC=2QO=8﹣6t
∴N点坐标为(3，8﹣6t)
由矩形对角线互相平分
∴点M坐标为(3t﹣1，8﹣5t)
当M在抛物线上时8﹣5t=﹣(3t﹣1)2+3(3t﹣1)+4,解得t=
当点Q到A时，Q在抛物线上，此时t=2
当N在抛物线上时，8﹣6t=4,∴t=eq \f(2,3)
综上所述当t=eq \f(2,3)、或2时，矩形PQNM的顶点落在抛物线上.
(1)证明：当x=0时，y=﹣eq \f(1,2)x2+eq \f(3,2)x+2=2，则C(0，2)；
当y=0时，﹣eq \f(1,2)x2+eq \f(3,2)x+2=0，解得x1=﹣1，x2=4，则A(4，0)，B(﹣1，0)，
∵BC2=12+22=5，AC2=42+22=20，AB2=25，
∴BC2+AC2=AB2，
∴△ABC为直角三角形，∠ACB=90°；
(2)解：∠NGF的度数不变化.
设AC的解析式为y=kx+b，
把A(4，0)，C(0，2)代入得
，解得，
∴直线AC的解析式为y=﹣eq \f(1,2)x+2，
∵抛物线的对称轴为直线x=eq \f(3,2)，∴M(eq \f(3,2)，eq \f(5,4))，
∵GN⊥NF，
∴∠GNF=90°，
∴∠BNG=∠MNF，
∵∠ACB=90°，
∴∠NBC=∠OCA，
而MN∥OC，
∴∠NMF=∠OCA，
∴∠NBG=∠NMF，
∴△NMF∽△NBG，
∴==eq \f(1,2)，
∴tan∠NGF==eq \f(1,2)，
∴∠NGF的度数为定值；
(3)解：作GH⊥x轴于H，FQ⊥x轴于Q，F(n，﹣eq \f(1,2)n+2)，
当G点在BC上，如图1，易得直线BC的解析式为y=2x+2，
则G(eq \f(1,2)m﹣1，m)，
∵∠GNF=90°，
∴∠GNH=∠NFQ，
∴Rt△NGH∽Rt△FNQ，
∴=，即=，∴m=2n﹣3，
当m=0时，2n﹣3=0，解得n=eq \f(3,2)；当m=2时，2n﹣3=2，解得n=eq \f(5,2)；
∴此时n的范围为eq \f(3,2)≤n≤eq \f(5,2)；
当点G在AC上，如图2，则eq \f(5,2)＜n≤4，则G(4﹣2m，m)，
易得Rt△NGH∽Rt△FNQ，
∴=，即=，∴m=，
综上所述，m与n的关系式为：m=2n﹣3(eq \f(3,2)≤n≤eq \f(5,2))或m=(eq \f(5,2)＜n≤4).
解：(1)∵点A(﹣1，0)、点B(0，3)，在抛物线上，
∴，解得：，
∴所求的抛物线解析式为y=x2+4x+3；
(2)设平移后抛物线的解析式为y=x2+4x+3+k．
∵它经过点(﹣5，6)，∴6=(﹣5)2+4(﹣5)+3+k．∴k=﹣2．
∴平移后抛物线的解析式为y=x2+4x+3﹣2=x2+4x+1．
配方，得y=(x+2)2﹣3．
∵a=1＞0，∴平移后的抛物线的最小值是﹣3．
(3)由(2)可知，BD=PQ=2，对称轴为x=﹣2．
又∵S△MBD=2S△MPQ，∴BD边上的高是PQ边上的高的2倍．
设M点坐标为(m，n)．
①当M点的对称轴的左侧时，则有0﹣m=2(﹣2﹣m)．
∴m=﹣4．∴n=(﹣4)2+4(﹣4)+1=1．∴M(﹣4，1)．
②当M点在对称轴与y轴之间时，则有0﹣m=2[m﹣(﹣2)]．
∴m=﹣eq \f(4,3)．∴n=(﹣eq \f(4,3))2+(﹣eq \f(16,3))+1=﹣2eq \f(5,9)．∴M(﹣eq \f(4,3)，﹣2eq \f(5,9))．
③当M点在y轴的右侧时，则有m=2[(m﹣(﹣2)]．
∴m=﹣4＜0，不合题意，应舍去．
综合上述，得所求的M点的坐标是(﹣4，1)或(﹣eq \f(4,3)，﹣2eq \f(5,9))．
解：(1)把A(﹣1，0)、B(3，0)代入y＝ax2﹣x＋c，得
，解得，
∴抛物线的解析式为y＝eq \f(1,2)x2﹣x﹣eq \f(3,2)；
∵OC＝OA＝1，
∴C(0，1)，
设直线AC的解析式为y＝kx＋1，则﹣k＋1＝0，解得k＝1，
∴直线AC的解析式为y＝x＋1．
(2)如图1，作EG⊥x轴交直线AC于点G，作EH⊥AD于点H.
设E(x，eq \f(1,2)x2﹣x﹣eq \f(3,2))(﹣1＜x＜3)，则G(x，x＋1)，
∴EG＝x＋1﹣(eq \f(1,2)x2﹣x﹣eq \f(3,2))＝﹣eq \f(1,2)x2＋2x＋eq \f(5,2)．
∵OA＝OC＝1，∠AOC＝90°，
∴∠OCA＝45°，AC＝eq \r(2)，
∵∠HGE＝∠OCA＝45°，
∴EH＝EG•sin45°＝eq \f(\r(2),2)(﹣eq \f(1,2)x2＋2x＋eq \f(5,2))，
∴S△ACE＝eq \f(1,2)×eq \r(2)×eq \f(\r(2),2)(﹣eq \f(1,2)x2＋2x＋eq \f(5,2))＝﹣eq \f(1,4)x2＋x＋eq \f(5,4)＝﹣eq \f(1,4)(x﹣2)2＋eq \f(9,4)，
∵﹣eq \f(1,4)＜0，且﹣1＜2＜3，
∴当x＝2时，S△ACE最大＝eq \f(9,4)，此时E(2，﹣eq \f(3,2))．
∴△ACE面积的最大值为eq \f(9,4)，此时点E的坐标为(2，﹣eq \f(3,2))．
(3)存在．
如图2，在直线AC上取一点A′，使它的横坐标为1，则A′(1，2)，AA′＝2eq \r(2)，
∴点A′即为抛物线平移后点A的对应点，
可知抛物线向右、向上各平移2个单位长度．
∵y＝eq \f(1,2)x2﹣x﹣eq \f(3,2)＝eq \f(1,2)(x﹣1)2﹣2，
∴平移后的抛物线为y＝eq \f(1,2)(x﹣3)2，其顶点坐标为(3，0)；
∵原抛物线与新抛物线都经过点B(3，0)，
∴点B即为新抛物线与原抛物线的交点F．
作A′K⊥x轴于点K，则∠AKA′＝∠FKA′＝90°，AK＝A′K＝FK＝2，
∴∠AA′K＝∠FA′K＝45°，
∴∠AA′F＝90°．
由，得或(不符合题意，舍去)，
∴D(5，6)，
∴FD＝2eq \r(10)．
①当FP1＝FD时，则点P1与点D关于点A′对称，
∴P1(﹣3，﹣2)；
②当P2D＝FD＝2eq \r(10)时，
∵CD＝eq \r(2)×5＝5eq \r(2)，
∴CP2＝5eq \r(2)﹣2eq \r(10)，
∴xp＝eq \f(\r(2),2)×(5eq \r(2)﹣2eq \r(10))＝5﹣2eq \r(5)，yp＝5﹣2eq \r(5)＋1＝6﹣2eq \r(5)，
P2(5﹣2eq \r(5)，6﹣2eq \r(5))；
③当DP3＝FP3时，
∵∠P3DF＝∠FDP1，∠DFP3＝∠DP1F，
∴△P3DF∽△FDP1，
∴，
∵DP1＝eq \r(2)×(5＋3)＝8eq \r(2)，
∴P3D＝＝＝，
∴CP3＝5eq \r(2)﹣eq \f(5\r(2),2)＝eq \f(5\r(2),2)，
∴xp＝eq \f(5\r(2),2)×eq \f(\r(2),2)＝eq \f(5,2)，yp＝eq \f(5,2)+1＝eq \f(7,2)，
∴P3(eq \f(5,2)，eq \f(7,2))；
④当P4D＝FD＝2eq \r(10)时，则CP4＝5eq \r(2)＋2eq \r(10)，
∴xp＝eq \f(\r(2),2)×(5eq \r(2)＋2eq \r(10))＝5＋2eq \r(5)，yp＝5＋2eq \r(5)＋1＝6＋2eq \r(5)，
∴P4(5＋2eq \r(5)，6＋2eq \r(5))．
综上所述，点P的坐标为(﹣3，﹣2)或(5﹣2eq \r(5)，6﹣2eq \r(5))或(eq \f(5,2)，eq \f(7,2))或(5＋2eq \r(5)，6＋2eq \r(5))．
解：(1)∵抛物线y=ax2＋bx＋c(a≠0)与x轴交于点A(1，0)和点B(﹣3，0)，
∴OB=3，
∵OC=OB，
∴OC=3，
∴c=3，
∴，解得：，
∴所求抛物线解析式为：y=﹣x2﹣2x＋3；
(2)如图2，过点E作EF⊥x轴于点F，设E(a，﹣a2﹣2a＋3)(﹣3＜a＜0)，
∴EF=﹣a2﹣2a＋3，BF=a＋3，OF=﹣a，
∴S四边形BOCE=eq \f(1,2)BF•EF＋eq \f(1,2)(OC＋EF)•OF，
=eq \f(1,2)(a＋3)•(﹣a2﹣2a＋3)＋eq \f(1,2)(﹣a2﹣2a＋6)•(﹣a)，
=﹣eq \f(3,2)a2﹣eq \f(9,2)a＋eq \f(9,2)=﹣eq \f(3,2)(a＋eq \f(3,2))2＋7eq \f(7,8)，
∴当a=﹣eq \f(3,2)时，S四边形BOCE最大，且最大值为7eq \f(7,8)．
此时，点E坐标为(﹣eq \f(3,2)，eq \f(15,4))；
(3)∵抛物线y=﹣x2﹣2x＋3的对称轴为x=﹣1，点P在抛物线的对称轴上，
∴设P(﹣1，m)，
∵线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，
①当m≥0时，
∴PA=PA1，∠APA1=90°，
如图3，过A1作A1N⊥对称轴于N，设对称轴于x轴交于点M，
∴∠NPA1＋∠MPA=∠NA1P＋∠NPA1=90°，
∴∠NA1P=∠NPA，
在△A1NP与△PMA中，
，
∴△A1NP≌△PMA，
∴A1N=PM=m，PN=AM=2，
∴A1(m﹣1，m＋2)，
代入y=﹣x2﹣2x＋3得：m＋2=﹣(m﹣1)2﹣2(m﹣1)＋3，
解得：m=1，m=﹣2(舍去)，
②当m＜0时，要使P2A=P2A，2，由图可知A2点与B点重合，
∵∠AP2A2=90°，∴MP2=MA=2，
∴P2(﹣1，﹣2)，
∴满足条件的点P的坐标为P(﹣1，1)或(﹣1，﹣2)．

解：(1)∵抛物线y＝a(x﹣3)(x＋6)过点A(﹣1，5)，
∴5＝﹣20a，
∴a＝﹣eq \f(1,4)，
∴抛物线的解析式为y＝﹣eq \f(1,4)(x﹣3)(x＋6)，
令y＝0，则﹣eq \f(1,4)(x﹣3)(x＋6)＝0，解得x＝3或﹣6，
∴C(3，0)，
当x＝﹣5时，y＝﹣eq \f(1,4)×(﹣8)×1＝2，
∴B(﹣5，2)，
∴m＝2．
(2)设P(t，0)，则有＝，
整理得，21t2＋242t＋621＝0，解得t＝﹣或﹣，
经检验t＝﹣或﹣是方程的解，
∴满足条件的点P坐标为(﹣，0)或(﹣，0)．
(3)存在．连接AB，设AB的中点为T．
①当直线CM经过AB的中点T时，满足条件．
∵A(﹣1，5)，B(﹣5，2)，TA＝TB，
∴T(﹣3，eq \f(7,2))，
∵C(3，0)，
∴直线CT的解析式为y＝﹣x＋，
由，解得 (即点C)或，
∴M(﹣，)，
②CM′∥AB时，满足条件，
∵直线AB的解析式为y＝x＋，
∴直线CM′的解析式为y＝eq \f(3,4)x﹣eq \f(9,4)，
由，解得 (即点C)或，
∴M′(﹣9，﹣9)，
综上所述，满足条件的点M的横坐标为﹣eq \f(11,3)或﹣9．