

所属成套资源:2024年中考数学二轮复习 二次函数压轴题 专项提升练习 (含答案)
2024年中考数学二轮复习 二次函数压轴题 专项提升练习一(含答案)
展开
这是一份2024年中考数学二轮复习 二次函数压轴题 专项提升练习一(含答案),共13页。试卷主要包含了①求抛物线的解析式,解得x1=﹣1,x2=2n+1等内容,欢迎下载使用。
如图,抛物线y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,直线l与抛物线交于点B,交y轴于点D(0,3).
(1)求该抛物线的函数表达式;
(2)点P(m,0)为线段OB上一动点,过点P作x轴的垂线EF,分别交抛物线于直线l于点E,F,连接CE,CF,BE,求四边形CEBF面积的最大值及此时m的值;
(3)点M为y轴右侧抛物线上一动点,过点M作直线MN∥AC交直线l于点N,是否存在点M,使以A,C,M,N四点为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
如图,抛物线y=ax2+2x+c的对称轴是直线x=1,与x轴交于点A,B(3,0),与y轴交于点C,连接AC.
(1)求此抛物线的解析式;
(2)已知点D是第一象限内抛物线上的一个动点,过点D作DM⊥x轴,垂足为点M,DM交直线BC于点N,是否存在这样的点N,使得以A,C,N为顶点的三角形是等腰三角形.若存在,请求出点N的坐标,若不存在,请说明理由;
(3)已知点E是抛物线对称轴上的点,在坐标平面内是否存在点F,使以点B、C、E、F为顶点的四边形为矩形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(-4,0)、B(0,3),抛物线y=-x2+2x+1与y轴交于点C.
(1)求直线y=kx+b的函数解析式;
(2)若点P(x,y)是抛物线y=-x2+2x+1上的任意一点,设点P到直线AB的距离为d,求d关于x的函数解析式,并求d取最小值时点P的坐标;
(3)若点E在抛物线y=-x2+2x+1的对称轴上移动,点F在直线AB上移动,求CE+EF的最小值.
以点P(n,n2+2n+1)(n≥1)为顶点的抛物线y=﹣x2+bx+c与x轴交于点A、B(点A在点B的左边).
(1)当n=1时,试求b和c的值;当n>1时,求b与n,c与n之间的关系式.
(2)若点P到AB的距离等于线段AB长的10倍,求此抛物线y=﹣x2+bx+c的解析式.
(3)设抛物线y=﹣x2+bx+c与y轴交于点D,O为原点,矩形OEFD的顶点E、F分别在x轴和该抛物线上,当矩形OEFD的面积为42时,求点P的坐标.
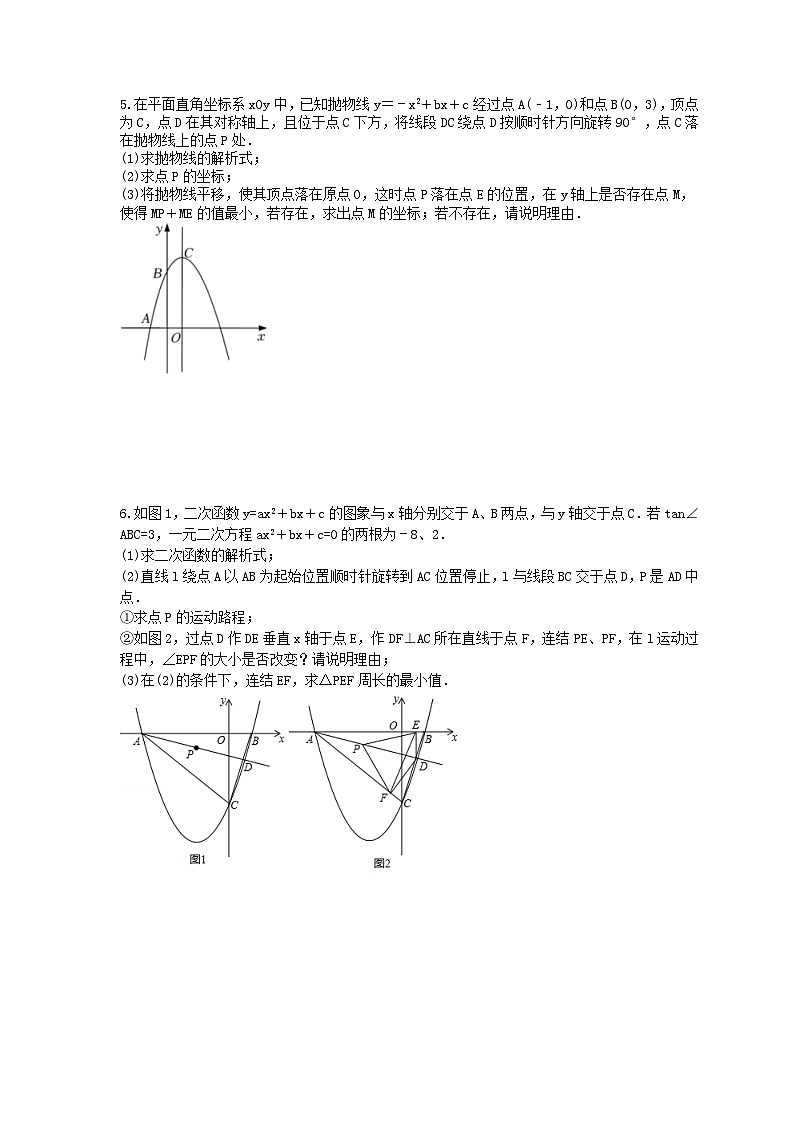
在平面直角坐标系xOy中,已知抛物线y=﹣x2+bx+c经过点A(﹣1,0)和点B(0,3),顶点为C,点D在其对称轴上,且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
(1)求抛物线的解析式;
(2)求点P的坐标;
(3)将抛物线平移,使其顶点落在原点O,这时点P落在点E的位置,在y轴上是否存在点M,使得MP+ME的值最小,若存在,求出点M的坐标;若不存在,请说明理由.
如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.
(1)求二次函数的解析式;
(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD中点.
①求点P的运动路程;
②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结EF,求△PEF周长的最小值.
已知抛物线y=﹣x2+bx+c经过点A(﹣1,2).
(1)抛物线顶点位于y轴右侧且纵坐标为6.①求抛物线的解析式.②如图1,直线y=﹣x+4与抛物线交于B、C两点,P为线段BC上一点,过P作PM∥y轴交抛物线于M点.若PM=3,求P点的坐标.
(2)将抛物线平移,使点A的对应点为A'(m+1,b+4),其中m≠2.若平移后的抛物线经过点N(2,1),平移后的抛物线顶点恰好落在直线y=x+5上,求b的值.
如图,已知二次函数y=x2+2x+c与x轴正半轴交于点B(另一个交点为A),与y轴负半轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)设直线AC的解析式为y=kx+b,求点A的坐标,并结合图象写出不等式x2+2x+c≥kx+b的解集;
(3)已知点P(﹣3,1),Q(2,2t+1),且线段PQ与抛物线y=x2+2x+c有且只有一个公共点,直接写出t的取值范围.
\s 0 答案
解:(1)将A(﹣1,0),B(3,0)代入y=ax2+bx﹣3中得:
.解得:.
∴该抛物线的函数表达式为:y=x2﹣2x﹣3.
(2)设直线l的解析式为y=kx+n,
将B(3,0),D(0,3)代入上式得:
.解得:.
∴直线l的解析式为:y=﹣x+3.
∵点P(m,0),EF⊥x轴,
∴E点坐标为(m,m2﹣2m﹣3),点F的坐标为(m,﹣m+3).
∴EF=﹣m+3﹣m2+2m+3=﹣m2+m+6.
∵B(3,0),
∴OB=3.
∵S四边形CEBF=S△CEF+S△BEF=eq \f(1,2)EF•OP+eq \f(1,2)•BP×EF=eq \f(1,2)FE•OB,
∴=﹣.
∵<0,
∴当m=eq \f(1,2)时,S四边形CEBF有最大值=.
即:当m=eq \f(1,2)时,四边形CEBF面积的最大值为.
(3)存在.①当点M在直线BD的下方时,如图,
令x=0,则y=﹣3.
∴C(0,﹣3).
∴OC=3.
∵A(﹣1,0),
∴OA=1.
过M作ME⊥y轴于E,过N作NF⊥ME于F,交x轴于点G,
∵四边形ACMN为平行四边形,
∴AC∥MN,AC=MN.
∵NF⊥ME,ME⊥OE,
∴NF∥OE.
∴∠ACO=∠MNF.
在△AOC和△MFN中,
.
∴△AOC≌△MFN(AAS).
∴NF=OC=3,MF=OA=1.
设M(h,h2﹣2h﹣3),则ME=h,GF=OE=﹣h2+2h+3.
∴OG=EF=ME﹣MF=h﹣1.
∴N(h﹣1,﹣h+4).
∴NG=﹣h+4,
∵NG+GF=NF=3,
∴﹣h+4﹣h2+2h+3=3.解得:h=(负数不合题意,舍去).
∴h=.∴M().
②当点M在直线BD的上方时,如图,
过N作NE⊥y轴于E,过M作MF⊥NE于F,交x轴于点G,
由①知:△MNF≌△CAO(AAS),可得NF=OA=1,MF=OC=3.
设M(h,h2﹣2h﹣3),则OG=FE=h,GM=h2﹣2h﹣3.
∴NE=EF+NF=h+1.
∴N(h+1,﹣h+2).
∴GF=OE=h﹣2.
∵MG+GF=MF=3,
∴h﹣2+h2﹣2h﹣3=3.解得:h=(负数不合题意,舍去).
∴h=.∴M().
综上所述,存在点M,使以A,C,M,N四点为顶点的四边形是平行四边形,此时点M的坐标为()或().
解:(1)抛物线y=ax2+2x+c的对称轴是直线x=1,与x轴交于点A,B(3,0),
∴A(﹣1,0),
∴,解得,
∴抛物线的解析式y=﹣x2+2x+3;
(2)∵y=﹣x2+2x+3,∴C(0,3),
设直线BC的解析式为y=kx+3,
将点B(3,0)代入得:0=3k+3,解得:k=﹣1,
∴直线BC的解析式为y=﹣x+3;
设点D坐标为(t,﹣t2+2t+3),则点N(t,﹣t+3),
∵A(﹣1,0),C(0,3),
∴AC2=12+32=10,
AN2=(t+1)2+(﹣t+3)2=2t2﹣4t+10,CN2=t2+(3+t﹣3)2=2t2,
①当AC=AN时,AC2=AN2,
∴10=2t2﹣4t+10,解得t1=2,t2=0(不合题意,舍去),
∴点N的坐标为(2,1);
②当AC=CN时,AC2=CN2,
∴10=2t2,解得t1=eq \r(5),t2=﹣eq \r(5) (不合题意,舍去),
∴点N的坐标为(eq \r(5),3﹣eq \r(5));
③当AN=CN时,AN2=CN2,
∴2t2﹣4t+10=2t2,解得t=eq \f(5,2),
∴点N的坐标为(eq \f(5,2),eq \f(1,2));
综上,存在,点N的坐标为(2,1)或(eq \r(5),3﹣eq \r(5))或(eq \f(5,2),eq \f(1,2));
(3)设E(1,a),F(m,n),
∵B(3,0),C(0,3),
∴BC=3eq \r(2),
①以BC为对角线时,BC2=CE2+BE2,
∴(3eq \r(2))2=12+(a﹣3)2+a2+(3﹣1)2,
解得:a=eq \f(3,2)+eq \f(1,2)eq \r(17),或a=eq \f(3,2)﹣eq \f(1,2)eq \r(17),∴E(1,eq \f(3,2)+eq \f(1,2)eq \r(17))或(1,eq \f(3,2)﹣eq \f(1,2)eq \r(17)),
∵B(3,0),C(0,3),
∴m+1=0+3,n+eq \f(3,2)+eq \f(1,2)eq \r(17)=0+3或n+eq \f(3,2)﹣eq \f(1,2)eq \r(17)=0+3,
∴m=2,n=eq \f(3,2)﹣eq \f(1,2)eq \r(17)或n=eq \f(3,2)+eq \f(1,2)eq \r(17),
∴点F的坐标为(2,eq \f(3,2)﹣eq \f(1,2)eq \r(17))或(2,eq \f(3,2)+eq \f(1,2)eq \r(17));
②以BC为边时,BE2=CE2+BC2或CE2=BE2+BC2,
∴a2+(3﹣1)2=12+(a﹣3)2+(3eq \r(2))2或12+(a﹣3)2=a2+(3﹣1)2+(3eq \r(2))2,
解得:a=4或a=﹣2,
∴E(1,4)或(1,﹣2),
∵B(3,0),C(0,3),
∴m+0=1+3,n+3=0+4或m+3=1+0,n+0=3﹣2,
∴m=4,n=1或m=﹣2,n=1,
∴点F的坐标为(4,1)或(﹣2,1),
综上所述:存在,点F的坐标为(2,eq \f(3,2)﹣eq \f(1,2)eq \r(17))或(2,eq \f(3,2)+eq \f(1,2)eq \r(17))或(4,1)或(﹣2,1).
解:(1)∵直线y=kx+b经过点A(-4,0),B(0,3),
∴eq \b\lc\{(\a\vs4\al\c1(0=-4k+b,3=b)),解得eq \b\lc\{(\a\vs4\al\c1(k=\f(3,4),b=3)),
∴直线的函数解析式为y=eq \f(3,4)x+3;
(2)如图,过点P作PM⊥AB于点M,作PN∥y轴交直线AB于点N.
∴∠PNM=∠ABO,
∵∠AOB=∠NMP=90°,
∴△AOB∽△PMN,∴eq \f(AO,PM)=eq \f(AB,PN),
∵OA=4,OB=3,
∴AB=eq \r(OA2+OB2)=5,
∴PM=eq \f(4,5)PN,
∵点P是抛物线上的点,PN∥y轴,
∴P(x,-x2+2x+1),N(x,eq \f(3,4)x+3),
∴PN=eq \f(3,4)x+3-(-x2+2x+1)=x2-eq \f(5,4)x+2=(x-eq \f(5,8))2+eq \f(103,64),PM=d=eq \f(4,5)(x-eq \f(5,8))2+eq \f(103,80),
∴当x=eq \f(5,8)时,PM取得最小值eq \f(103,80),此时P点坐标为(eq \f(5,8),eq \f(119,64));
(3)∵抛物线y=-x2+2x+1与y轴交于点C,
∴C(0,1),对称轴为直线x=-eq \f(2,2×(-1))=1,
如解图,作点C关于对称轴的对称点G,则G点坐标为(2,1),
点G到直线AB的距离即为CE+EF的最小值,最小值为d=eq \f(4,5)×(2-eq \f(5,8))2+eq \f(103,80)=eq \f(14,5).
解:(1)当n=1时,点P坐标为(1,4),
则y=﹣(x﹣1)2+4=﹣x2+2x+3=﹣x2+bx+c,
解得:b=2,c=3.
当n>1时,则y=﹣(x﹣n)2+n2+2n+1=﹣x2+2nx+2n+1=﹣x2+bx+c,
所以b=2n,c=2n+1.
(2)∵y=﹣(x﹣n)2+n2+2n+1=﹣x2+2nx+2n+1,
∴当y=0时,即﹣x2+2nx+2n+1=0.解得x1=﹣1,x2=2n+1.
由于点A在点B的左边,
∴A(﹣1,0)、B(2n+1,0),即AB=2n+1﹣(﹣1)=2n+2.
又∵点P到x轴的距离为n2+2n+1,
∴有n2+2n+1=10(2n+2).
解得n=19或n=﹣1(不合,舍去),即n=19.
故此时抛物线的解析式为y=﹣x2+38x+39.
(3)如图所示,
∵c=2n+1,∴D(0,2n+1),即OD=2n+1.
又DF∥x轴,且D、F关于直线x=n对称,
∴F(2n,2n+1).有DF=2n.从而OD•DF=2n(2n+1)=42,
解得n=3或n=-eq \f(7,2)(不合,舍去),即n=3.
故点P的坐标为(3,16).
解:(1)把A(﹣1,0)和点B(0,3)代入y=﹣x2+bx+c,
得,解得:,
∴抛物线解析式为y=﹣x2+2x+3;
(2)∵y=﹣(x﹣1)2+4,
∴C(1,4),抛物线的对称轴为直线x=1,
如图,设CD=t,则D(1,4﹣t),
∵线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处,
∴∠PDC=90°,DP=DC=t,
∴P(1+t,4﹣t),
把P(1+t,4﹣t)代入y=﹣x2+2x+3得:
﹣(1+t)2+2(1+t)+3=4﹣t,
整理得t2﹣t=0,解得:t1=0(舍去),t2=1,
∴P(2,3);
(3)∵P点坐标为(2,3),顶点C坐标为(1,4),将抛物线平移,使其顶点落在原点O,这时点P落在点E的位置,
∴E点坐标为(1,﹣1),
∴点E关于y轴的对称点F(﹣1,﹣1),
连接PF交y轴于M,则MP+ME=MP+MF=PF的值最小,
设直线PF的解析式为y=kx+n,
∴,解得:,
∴直线PF的解析式为y=eq \f(4,3)x+eq \f(1,3),
∴点M的坐标为(0,eq \f(1,3)).
解:(1)∵函数y=ax2+bx+c与x轴交于A、B两点,且一元二次方程ax2+bx+c=0两根为:﹣8,2,∴A(﹣8,0)、B(2,0),即OB=2,
又∵tan∠ABC=3,
∴OC=6,即C(0,﹣6),
将A(﹣8,0)、B(2,0)代入y=ax2+bx﹣6中,得:
,解得:,
∴二次函数的解析式为:y=eq \f(3,8)x2+eq \f(9,4)x﹣6;
(2)①如图1,当l在AB位置时,P即为AB的中点H,
当l运动到AC位置时,P即为AC中点K,
∴P的运动路程为△ABC的中位线HK,∴HK=eq \f(1,2)BC,
在Rt△BOC中,OB=2,OC=6,
∴BC=2eq \r(10),
∴HK=eq \r(10),即P的运动路程为:eq \r(10);
②∠EPF的大小不会改变,理由如下:如图2,∵DE⊥AB,
∴在Rt△AED中,P为斜边AD的中点,∴PE=eq \f(1,2)AD=PA,
∴∠PAE=∠PEA=eq \f(1,2)∠EPD,同理可得:∠PAF=∠PFA=eq \f(1,2)∠DPF,
∴∠EPF=∠EPD+∠FPD=2(∠PAE+∠PAF),即∠EPF=2∠EAF,
又∵∠EAF大小不变,
∴∠EPF的大小不会改变;
(3)设△PEF的周长为C,则C△PEF=PE+PF+EF,
∵PE=eq \f(1,2)AD,PF=eq \f(1,2)AD,∴C△PEF=AD+EF,
在等腰三角形PEF中,如图2,过点P作PG⊥EF于点G,
∴∠EPG=eq \f(1,2)∠EPF=∠BAC,
∵tan∠BAC==eq \f(3,4),∴tan∠EPG==eq \f(3,4),
∴EG=eq \f(3,5)PE,EF=eq \f(6,5)PE=eq \f(3,5)AD,
∴C△PEF=AD+EF=(1+eq \f(3,5))AD=eq \f(8,5)AD,
又当AD⊥BC时,AD最小,此时C△PEF最小,
又S△ABC=30,∴eq \f(1,2)BC×AD=30,∴AD=3eq \r(10),
∴C△PEF最小值为:eq \f(8,5)AD=eq \r(10).
解:(1)①将点A(﹣1,2)代入y=﹣x2+bx+c,
∴c﹣b=3,
∵抛物线的顶点纵坐标为6,
∴=6,
∴c=﹣3或c=5,
∴b=﹣6或b=2,
∵顶点位于y轴右侧,
∴b>0,
∴b=2,
∴y=﹣x2+2x+5;
②设M(t,﹣t2+2t+5),则P(t,﹣t+4),
∴PM=﹣t2+3t+1,
∵PM=3,
∴﹣t2+3t+1=3,
解得t=1或t=2,
∴P(1,3)或(2,2);
(2)∵点A(﹣1,2)平移后对应点为A'(m+1,b+4),
∴抛物线向右平移m+2个单位,向上平移b+2个单位,
∵c﹣b=3,
∴y=﹣x2+bx+c=﹣(x﹣eq \f(1,2)b)2+b+3+eq \f(1,4)b2,
∴平移后的抛物线解析为y=﹣(x﹣eq \f(1,2)b﹣m﹣2)2+2b+5+eq \f(1,4)b2,
∴抛物线的顶点为(eq \f(1,2)b+m+2,2b+5+eq \f(1,4)b2),
∵抛物线顶点恰好落在直线y=x+5上,
∴eq \f(1,2)b+m+2+5=2b+5+eq \f(1,4)b2,
∴m=eq \f(1,4)b2+b﹣2①,
∵平移后的抛物线经过点N(2,1),
∴﹣(﹣eq \f(1,2)b﹣m)2+2b+5+eq \f(1,4)b2=1②,
由①②可得,b+2m=b+4或b+2m=﹣b﹣4,
当b+2m=b+4时,m=2,此时不符合题意;
当b+2m=﹣b﹣4时,b=0或b=﹣10,
当b=0时,m=﹣2;当b=﹣10时,m=8;
∴b的值为0或﹣10.
解:(1)设B(m,0),则OB=m,
∵OC=3OB,
∴OC=3m,C(0,﹣3m),
将B(m,0),C(0,﹣3m)代入y=x2+2x+c得:
,解得(此时B不在x轴正半轴,舍去)或,
∴抛物线的解析式为y=x2+2x﹣3;
(2)在y=x2+2x﹣3中,令y=0得x2+2x﹣3=0,解得x=﹣3或x=1,
∴A(﹣3,0),
由图象可知,当x≤﹣3或x≥0时,抛物线在直线上方,即x2+2x+c≥kx+b,
∴不等式x2+2x+c≥kx+b的解集为x≤﹣3或x≥0;
(3)设直线x=2与抛物线y=x2+2x﹣3交于K,如图:
由图可知,当Q在K及K下方时,线段PQ与抛物线y=x2+2x﹣3有且只有一个公共点,
在y=x2+2x﹣3中,令x=2得y=22+2×2﹣3=5,
∴2t+1≤5,解得t≤2,
答:线段PQ与抛物线y=x2+2x+c有且只有一个公共点,t的取值范围是t≤2.
相关试卷
这是一份2024年中考数学二轮复习 二次函数压轴题 专项提升练习10(含答案),共12页。
这是一份2024年中考数学二轮复习 二次函数压轴题 专项提升练习09(含答案),共14页。试卷主要包含了以PQ,QM为边作矩形PQMN等内容,欢迎下载使用。
这是一份2024年中考数学二轮复习 二次函数压轴题 专项提升练习07(含答案),共13页。试卷主要包含了画图象如图所示等内容,欢迎下载使用。









