初中数学北师大版七年级上册3.3 整式同步练习题

这是一份初中数学北师大版七年级上册3.3 整式同步练习题，共15页。试卷主要包含了图形类探究，程序框图类，数字类探究等内容，欢迎下载使用。
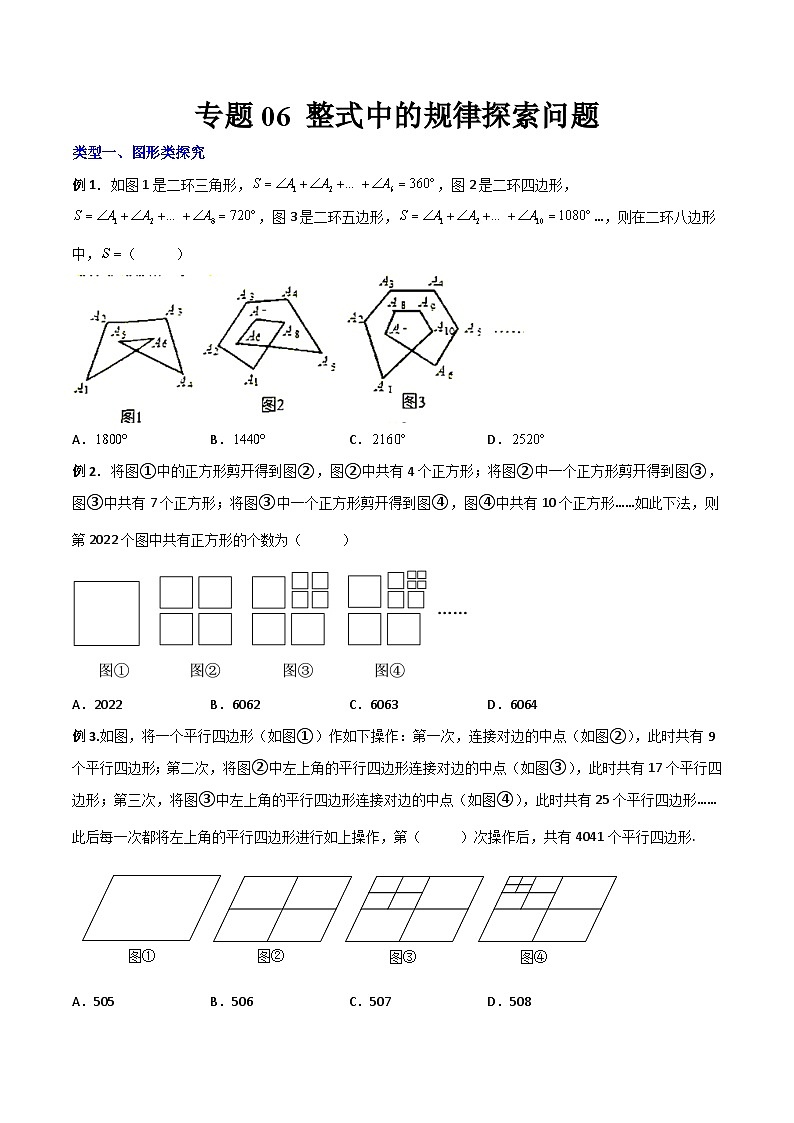
例1．如图1是二环三角形，，图2是二环四边形，，图3是二环五边形，…，则在二环八边形中，（ ）
A．B．C．D．
例2．将图①中的正方形剪开得到图②，图②中共有4个正方形；将图②中一个正方形剪开得到图③，图③中共有7个正方形；将图③中一个正方形剪开得到图④，图④中共有10个正方形……如此下法，则第2022个图中共有正方形的个数为（ ）
A．2022B．6062C．6063D．6064
例3.如图，将一个平行四边形（如图①）作如下操作：第一次，连接对边的中点（如图②），此时共有9个平行四边形；第二次，将图②中左上角的平行四边形连接对边的中点（如图③），此时共有17个平行四边形；第三次，将图③中左上角的平行四边形连接对边的中点（如图④），此时共有25个平行四边形……此后每一次都将左上角的平行四边形进行如上操作，第（ ）次操作后，共有4041个平行四边形.
A．505B．506C．507D．508
【变式训练1】中国古代十进位制的算筹记数法在世界数学史上是一个伟大的创造．据史料推测，算筹最晚出现在春秋晚期战国初年．1至9这9个数字的纵式和横式的表示数码如下图所示，算筹记数的方法为：个位用纵式，十位用横式，百位再用纵式，千位再用横式…，以此类推，就可以用算筹表示出任意大的自然数了．
根据上述材料，的运算结果可用算筹表示为（ ）
A．B．C．D．
【变式训练2】观察下列树枝分权的规律图，若第n个图树枝数用Yn表示，则Y8﹣Y4的值为（ ）
A．8×24B．15×24C．31×24D．33×24
【变式训练3】有边长为1的等边三角形卡片若干张，使用这些三角形卡片拼出边长分别是2，3，4…的等边三角形（如图），根据图形推断每个等边三角形卡片总数S与边长n的关系式_________．
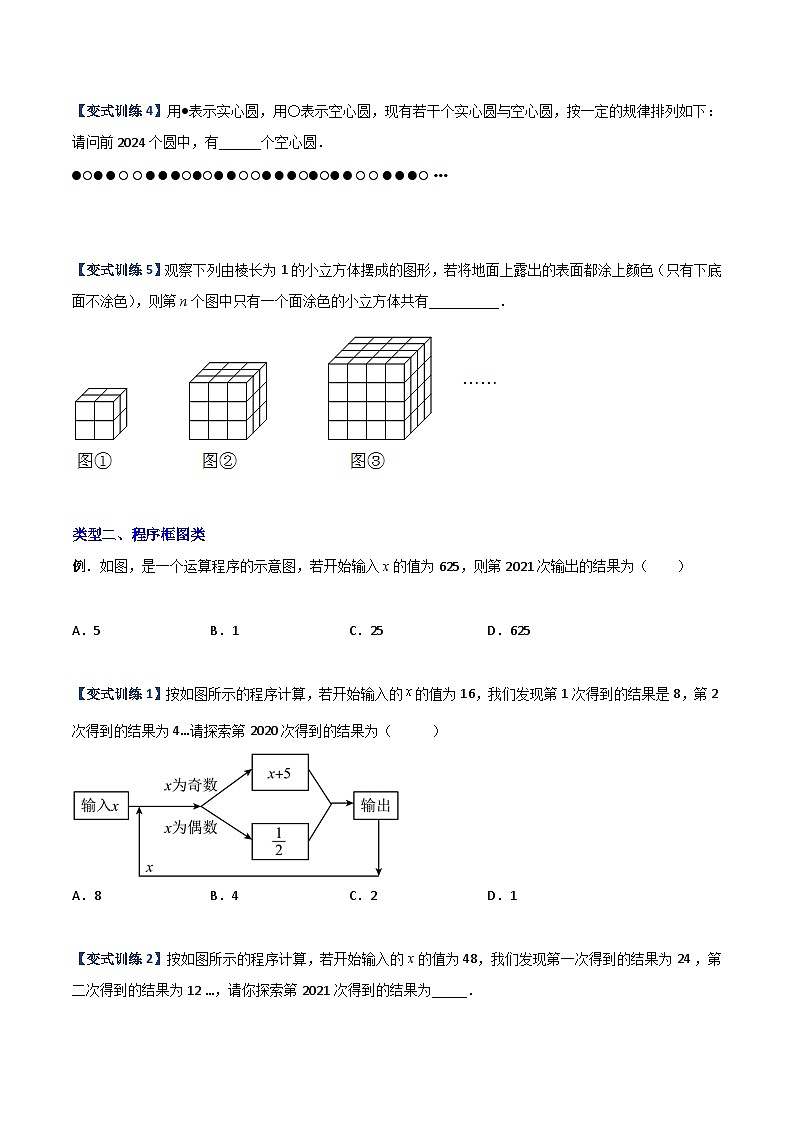
【变式训练4】用●表示实心圆，用〇表示空心圆，现有若干个实心圆与空心圆，按一定的规律排列如下：请问前2024个圆中，有______个空心圆．
【变式训练5】观察下列由棱长为1的小立方体摆成的图形，若将地面上露出的表面都涂上颜色（只有下底面不涂色），则第n个图中只有一个面涂色的小立方体共有__________．
类型二、程序框图类
例．如图，是一个运算程序的示意图，若开始输入x的值为625，则第2021次输出的结果为（ ）
A．5B．1C．25D．625
【变式训练1】按如图所示的程序计算，若开始输入的的值为16，我们发现第1次得到的结果是8，第2次得到的结果为4…请探索第2020次得到的结果为（ ）
A．8B．4C．2D．1
【变式训练2】按如图所示的程序计算，若开始输入的x的值为48，我们发现第一次得到的结果为24 ，第二次得到的结果为12 …，请你探索第2021次得到的结果为_____．
类型三、数字类探究
例1．生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型．在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型2n来表示．即：21＝2，22＝4，23＝8，24＝16，25＝32，……，请你推算22022的个位数字是（ ）
A．8B．6C．4D．2
例2．已知一列数：1，，3，，5，，7，…将这列数排成下列形式：
第1行 1
第2行 3
第3行 5
第4行 7 9
第5行 11 13 15
… …
按照上述规律排下去，那么第10行从左边数第5个数等于（ ）
A．B．C．45D．
例3．计算=____.
【变式训练1】观察：第1个等式，第2个等式，第3个等式，第4个等式…猜想：第n个等式是________.
【变式训练2】一组数按照这样的规律排列：第十个数是______．
【变式训练3】已知，在计算：的过程中，如果存在正整数N，使得各个数位均不产生进位，那么称这样的正整数N为“本位数”．例如：2和30都是“本位数”，因为没有进位，没有进位：15和91都不是“本位数”，因为，个位产生进位，，十位产生进位．根据上面给出的材料：在所有三位数中，“本位数”一共有_______个．
【变式训练4】如图所示的是中国南宋数学家杨辉在详解《九童算法》中出现的三角形状的数列，又称为“杨辉三角”．该三角形中的数据排列有着一定的规律，第21行从左边数第19个数是（ ）
A．19B．380C．210D．190
专题06 整式中的规律探索问题
类型一、图形类探究
例1．如图1是二环三角形，，图2是二环四边形，，图3是二环五边形，…，则在二环八边形中，（ ）
A．B．C．D．
【答案】C
【详解】解：依题意可知，二环三角形，S=360°， 二环四边形，S=720°=360°×2=360°×（4-2），
二环五边形，S=1080°=360°×3=360°×（5-2）， … 二环n边形（n≥3的整数）中，S=360°×（n-2），
二环八边形中，S=360°×（8-2）=2160°，
故选：C．
例2．将图①中的正方形剪开得到图②，图②中共有4个正方形；将图②中一个正方形剪开得到图③，图③中共有7个正方形；将图③中一个正方形剪开得到图④，图④中共有10个正方形……如此下法，则第2022个图中共有正方形的个数为（ ）
A．2022B．6062C．6063D．6064
【答案】D
【详解】解：图①中的正方形剪开得到图②，图②中共有3×1+1=4个正方形；
将图②中一个正方形剪开得到图③，图③中共有3×2+1=7个正方形；
将图③中一个正方形剪开得到图④，图④中共有3×3+1=10个正方形；……；
发现规律：第n个图中共有正方形的个数为：3（n-1）+1=3n-2；
则第2022个图中共有正方形的个数为3×2022-2=6064．故选：D．
例3.如图，将一个平行四边形（如图①）作如下操作：第一次，连接对边的中点（如图②），此时共有9个平行四边形；第二次，将图②中左上角的平行四边形连接对边的中点（如图③），此时共有17个平行四边形；第三次，将图③中左上角的平行四边形连接对边的中点（如图④），此时共有25个平行四边形……此后每一次都将左上角的平行四边形进行如上操作，第（ ）次操作后，共有4041个平行四边形.
A．505B．506C．507D．508
【答案】A
【详解】解：第一次操作后，共有9=1+8个平行四边形，
第二次操作后，共有17=1+8×2个平行四边形，
第三次操作后，共有25=1+8×3个平行四边形，……
则第n次操作后，共有（1+8n）个平行四边形，
由1+8n=4041得n=505，
即第505次操作后，共有4041个平行四边形.
故选：A .
【变式训练1】中国古代十进位制的算筹记数法在世界数学史上是一个伟大的创造．据史料推测，算筹最晚出现在春秋晚期战国初年．1至9这9个数字的纵式和横式的表示数码如下图所示，算筹记数的方法为：个位用纵式，十位用横式，百位再用纵式，千位再用横式…，以此类推，就可以用算筹表示出任意大的自然数了．
根据上述材料，的运算结果可用算筹表示为（ ）
A．B．C．D．
【答案】D
【详解】解：，
根据题意，6、2、5，表示如下：
故选：D
【变式训练2】观察下列树枝分权的规律图，若第n个图树枝数用Yn表示，则Y8﹣Y4的值为（ ）
A．8×24B．15×24C．31×24D．33×24
【答案】B
【详解】解：由图可得到：
……
则：，
∴，故B正确．
故选：B．
【变式训练3】有边长为1的等边三角形卡片若干张，使用这些三角形卡片拼出边长分别是2，3，4…的等边三角形（如图），根据图形推断每个等边三角形卡片总数S与边长n的关系式_________．
【答案】S=n2（n≥1）
【详解】解：图1中，当n=2时，S=4．
图2中，当n=3时，S=9．
图3中，当n=4时，S=16．
…．
依此类推，总数S与边长n的关系式S=n2（n≥1）．
故答案为：S=n2（n≥1）
【变式训练4】用●表示实心圆，用〇表示空心圆，现有若干个实心圆与空心圆，按一定的规律排列如下：请问前2024个圆中，有______个空心圆．
【答案】809
【详解】解：观察图形，每10个图形循环一次，每一个循环中有6个实心圆，4个空心圆，
2024÷10=，
空心圆个数=4×202+1=808+1=809，
故答案为：809．
【变式训练5】观察下列由棱长为1的小立方体摆成的图形，若将地面上露出的表面都涂上颜色（只有下底面不涂色），则第n个图中只有一个面涂色的小立方体共有__________．
【答案】##
【详解】解：观察图形可知图①中，只有一个面涂色的小立方体共有0个，
图②中，只有一个面涂色的小立方体共有个，
图③中，只有一个面涂色的小立方体共有个，
……
则第n个图中只有一个面涂色的小立方体共有
故答案为：
类型二、程序框图类
例．如图，是一个运算程序的示意图，若开始输入x的值为625，则第2021次输出的结果为（ ）
A．5B．1C．25D．625
【答案】A
【详解】解：根据题意得：第一次输出的结果： ，
第二次输出的结果： ，第三次输出的结果： ，
第四次输出的结果： ，第五次输出的结果： ，
第六次输出的结果： ，第七次输出的结果： ，第八次输出的结果： ，
由此得到规律，从第四次开始奇数次输出为5，偶数次输出为1，
∴第2021次输出结果为5．
故选：A
【变式训练1】按如图所示的程序计算，若开始输入的的值为16，我们发现第1次得到的结果是8，第2次得到的结果为4…请探索第2020次得到的结果为（ ）
A．8B．4C．2D．1
【答案】D
【详解】解：第1次得到的结果为16×＝8，第2次得到的结果为8×＝4，
第3次得到的结果为4×＝2，第4次得到的结果为2×＝1，
第5次得到的结果为1+5＝6，第6次得到的结果为6×＝3，
第7次得到的结果为3＋5＝8，第8次得到的结果为8×=4，
第9次得到的结果为4×＝2，第10次得到的结果为2×＝1，
第11次的到的结果为1＋5＝6，第12次得到的结果为6×＝3，……
∴结果是8，4，2，1，6，3六个数为周期的循环，
∵2020÷6＝336…4，∴第2020次得到的结果为1，故选D．
【变式训练2】按如图所示的程序计算，若开始输入的x的值为48，我们发现第一次得到的结果为24 ，第二次得到的结果为12 …，请你探索第2021次得到的结果为_____．
【答案】8
【详解】按照程序，每次得到结果如下：
第1次：24
第2次：12
第3次：6
第4次：3
第5次：8
第6次：4
第7次：2
第8次：1
第9次：6
第10次：3
第11次：8……
根据以上结果以可发现，从第3次开始，结果按6、3、8、4、2、1每6个结果为一个周期进行循环，
∵……3，∴到2021次时，结果为循环中第3个数，结果为8，故答案为：8
类型三、数字类探究
例1．生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型．在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型2n来表示．即：21＝2，22＝4，23＝8，24＝16，25＝32，……，请你推算22022的个位数字是（ ）
A．8B．6C．4D．2
【答案】C
【详解】解：∵21＝2，22＝4，23＝8，24＝16，25＝32，…，
∴尾数每4个一循环，
∵2022÷4＝505……2，
∴22022的个位数字应该是：4．
故选：C．
例2．已知一列数：1，，3，，5，，7，…将这列数排成下列形式：
第1行 1
第2行 3
第3行 5
第4行 7 9
第5行 11 13 15
… …
按照上述规律排下去，那么第10行从左边数第5个数等于（ ）
A．B．C．45D．
【答案】A
【详解】解：第1行有1个数，绝对值为1＝，且是正数；
第2行有2个数，第一个数的绝对值为2＝，且为负数，且奇数为正，偶数为负；
第3行有3个数，第一个数的绝对值为4＝，且为负数，且奇数为正，偶数为负；
第4行有4个数，第一个数的绝对值为7＝，且为正数，且奇数为正，偶数为负；……
由上可知，第n行有n个数，此行第一个数的绝对值为；且奇数为正，偶数为负，
∴第10行从左边数第1个数绝对值为46，从左边数第5个数等于﹣50．
故选：A
例3．计算=____.
【答案】
【详解】解：设a=，b=，
则原式=a(1+b)-b(1+a)=a+ab-b-ab=a-b
=-=，
故答案为：．
【变式训练1】观察：第1个等式，第2个等式，第3个等式，第4个等式…猜想：第n个等式是________.
【答案】（2n-1）（2n+1）=（2n）2-1
【详解】解：第1个等式，第2个等式，
第3个等式，第4个等式，第n个等式（2n-1）（2n+1）=（2n）2-1；
故答案为：（2n-1）（2n+1）=（2n）2-1．
【变式训练2】一组数按照这样的规律排列：第十个数是______．
【答案】
【详解】解：找规律：发现了分母上的数字是分子的数的平方加1，
所以该组的数位： （n为组数），
当n=10时，原式=，所以第十个数是，
故答案为：．
【变式训练3】已知，在计算：的过程中，如果存在正整数N，使得各个数位均不产生进位，那么称这样的正整数N为“本位数”．例如：2和30都是“本位数”，因为没有进位，没有进位：15和91都不是“本位数”，因为，个位产生进位，，十位产生进位．根据上面给出的材料：在所有三位数中，“本位数”一共有_______个．
【答案】36
【详解】解：根据题意，可得：要想构成“本位数”，百位可以为1，2，3，十位可以为0，1，2，3，个位可以为0、1、2，所有的三位数中，“本位数”一共有（个）．
故答案为：36．
【变式训练4】如图所示的是中国南宋数学家杨辉在详解《九童算法》中出现的三角形状的数列，又称为“杨辉三角”．该三角形中的数据排列有着一定的规律，第21行从左边数第19个数是（ ）
A．19B．380C．210D．190
【答案】D
【详解】
解：第21行从左边数第19个数即为从右边数第三个
第3行右边数第三个数为1，即
第4行右边数第三个数为3，即
第5行右边数第三个数为6，即
第6行右边数第三个数为10，即
……
第21行右边数第三个数为21，即．
故选D．