北师大版2023-2024学年七年级数学上册压轴题攻略(成都专用)期末考试B卷压轴题考点训练(一)(原卷版+解析)

这是一份北师大版2023-2024学年七年级数学上册压轴题攻略(成都专用)期末考试B卷压轴题考点训练(一)(原卷版+解析)，共13页。

20．已知数轴上的点A，B表示的数分别为，4，P为数轴上任意一点，表示的数为x，若点P到点A，B的距离之和为7，则x的值为 _____．
21．我们知道在9点整时，时钟的分针与时针恰好互相垂直，那么从9点开始，到10点之前，经过__________分钟后，时钟的时针与分针的夹角为105°．
22．如图，红黄绿三块一样大的正方形纸片放在一个正方形盒内，它们之间互相重叠．已知露在外面的部分中，红色的面积是20，黄色的面积是13，绿色的面积是11，则正方形盒子的面积为_____________．
23．若关于x的方程，无论k为任何数时，它的解总是，那么_______．
24．如图，一把长度为5个单位的直尺AB放置在如图所示的数轴上（点A在点B左侧），点A、B、C表示的数分别是a、b、c，若b、c同时满足：
①c﹣b＝3；②（b﹣6）+3＝0是关于x的一元一次方程．
（1）a＝ ，b＝ ，c＝ ．
（2）设直尺以2个单位/秒的速度沿数轴匀速向右移动，同时点P从点A出发，以m个单位/秒的速度也沿数轴匀速向右移动，设运动时间为t秒．
①若B、P、C三点恰好在同一时刻重合，求m的值；
②当t＝1时，B、P、C三个点中恰好有一个点到另外两个点的距离相等，请直接写出所有满足条件的m的值．
25．我国著名数学家华罗庚说过“数缺形时少直观，形少数时难入微”．数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．
例如，式子的几何意义是数轴上所对应的点与2所对应的点之间的距离；因为，所以的几何意义就是数轴上所对应的点与-1所对应的点之间的距离．
结合数轴与绝对值的知识回答下列问题：
（1）若，则 ；的最小值是 ．
（2）若，则的值为 ；若，则的值为 ．
（3）是否存在使得取最小值，若存在，直接写出这个最小值及此时的取值情况；若不存在，请说明理由．
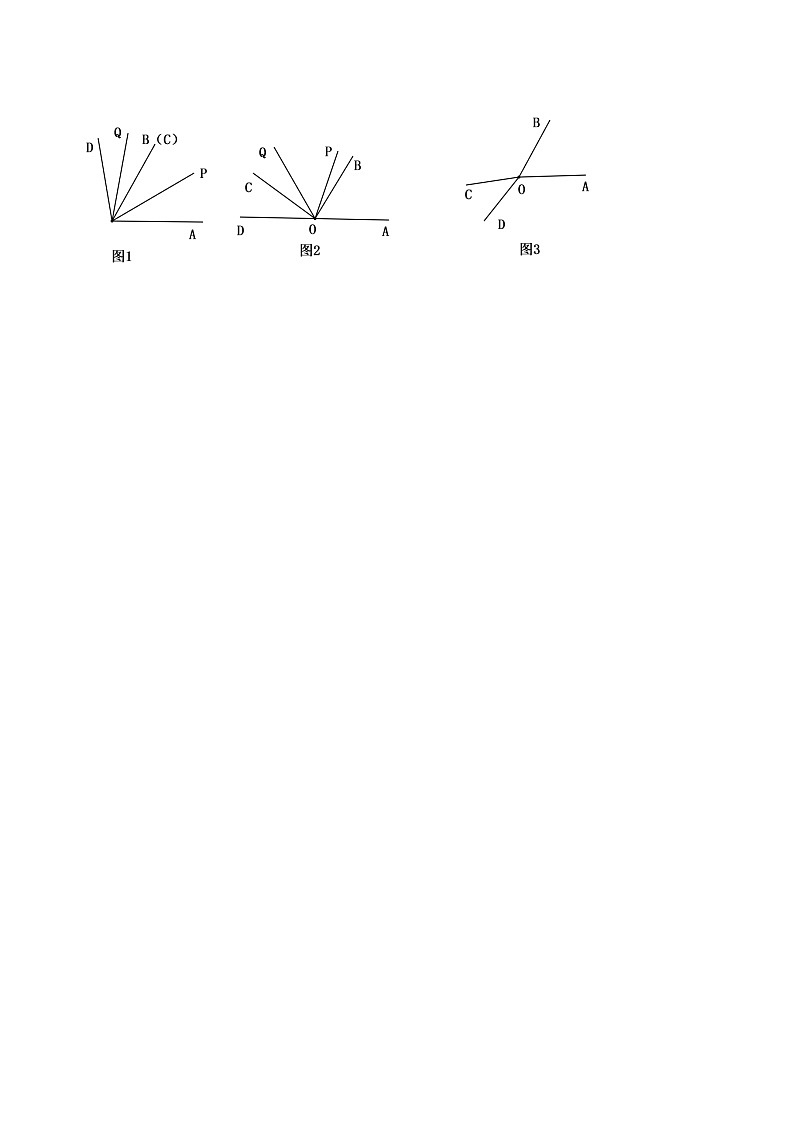
26．已知∠AOB和∠COD均为锐角，∠AOB＞∠COD，OP平分∠AOC，OQ平分∠BOD，将∠COD绕着点O逆时针旋转，使∠BOC=α（0≤α＜180°）
（1）若∠AOB=60°，∠COD=40°，
①当α=0°时，如图1，则∠POQ= ；
②当α=80°时，如图2，求∠POQ的度数；
③当α=130°时，如图3，请先补全图形，然后求出∠POQ的度数；
（2）若∠AOB=m°，∠COD=n°，m＞n，则∠POQ= ，（请用含m、n的代数式表示）．
期末考试B卷模拟训练（一）
19．如图，在三角形中，，点为边上一个动点，连接，把三角形沿着折叠，当时，则______．
【答案】33°或53°
【详解】解：当CA´在∠ACB外部，如图：
∵，，
∴，
∵三角形沿着折叠，
∴，
∴；
当CA´在∠ACB内部，如图：
∵，，
∴，
∵三角形沿着折叠，
∴，
∴；
故答案为：33°或53°
20．已知数轴上的点A，B表示的数分别为，4，P为数轴上任意一点，表示的数为x，若点P到点A，B的距离之和为7，则x的值为 _____．
【答案】或4.5
【详解】解：根据题意得：|x+2|+|x-4|=7，
当x＜-2时，化简得：-x-2-x+4=7，解得：x=-2.5；
当-2≤x＜4时，化简得：x+2-x+4=7，无解；
当x≥4时，化简得：x+2+x-4=7，解得：x=4.5，
综上，x的值为-2.5或4.5．
故答案为：-2.5或4.5．
21．我们知道在9点整时，时钟的分针与时针恰好互相垂直，那么从9点开始，到10点之前，经过__________分钟后，时钟的时针与分针的夹角为105°．
【答案】或30
【详解】解：分针的旋转速度是度/分钟，时针的旋转速度是0.5度/分钟，设经过x分钟后，时钟的时针与分针的夹角为105°，
分两种情况：
如图：
此时，∠AOC=0.5x，∠BOD=6x，
则∠COD=∠AOB+∠BOD-∠AOC= 90°+6x-0.5x=105°，
解得x=；如图：
此时，∠AOC=0.5x，∠BOD=360°-6x，
则∠COD=∠BOD-∠AOB+∠AOC=360°-6x -90°+0.5x=105°，解得x=30；
综上，经过或30分钟后，时钟的时针与分针的夹角为105°，
故答案为：或30
22．如图，红黄绿三块一样大的正方形纸片放在一个正方形盒内，它们之间互相重叠．已知露在外面的部分中，红色的面积是20，黄色的面积是13，绿色的面积是11，则正方形盒子的面积为_____________．
【答案】
【详解】解∶如图，将黄色部分向左平移，
∴黄色部分减少的面积为绿色部分增加的面积，
∵红黄绿三块一样大的正方形，整个盒子为正方形，
∴平移后，黄色部分与绿色部分面积相等，
∴平移前，黄色的面积是13，绿色的面积是11，
∴平移后黄色部分与绿色部分面积为∶ ( 13+11) 2=12，
设大正方形边长为b，红色部分边长为a，则黄色部分和绿色部分的长为a，宽为b-a，
∴，
∴，
∴，
∴，
故答案为∶．
23．若关于x的方程，无论k为任何数时，它的解总是，那么_______．
【答案】
【详解】解：将代入，
，
，
由题意可知：无论为任何数时恒成立，
，
，，
，
故答案为：
【点睛】本题主要考查了一元一次方程，解题的关键是正确理解一元一次方程的解．
24．如图，一把长度为5个单位的直尺AB放置在如图所示的数轴上（点A在点B左侧），点A、B、C表示的数分别是a、b、c，若b、c同时满足：
①c﹣b＝3；②（b﹣6）+3＝0是关于x的一元一次方程．
（1）a＝ ，b＝ ，c＝ ．
（2）设直尺以2个单位/秒的速度沿数轴匀速向右移动，同时点P从点A出发，以m个单位/秒的速度也沿数轴匀速向右移动，设运动时间为t秒．
①若B、P、C三点恰好在同一时刻重合，求m的值；
②当t＝1时，B、P、C三个点中恰好有一个点到另外两个点的距离相等，请直接写出所有满足条件的m的值．
【答案】（1）-1，4，7；（2）①；②6或7或7.5或8或9
【详解】解：（1）依题意有，
解得b＝4，c＝7，则a＝4﹣5＝﹣1．
故答案为：﹣1，4，7；
（2）①BC＝3，AC＝8，
当B、C重合时，
依题意有2t＝3，
解得t＝，
依题意有m＝8，
解得m＝．
②7﹣4﹣2＝1，
当B是P、C中点时，
依题意有5+2﹣m＝1，
解得m＝6；
当B与P重合时，
依题意有m﹣2＝5，
解得m＝7；
当P是B、C中点时，
依题意有m﹣＝5+2，
解得m＝7.5；
当P与C重合时，
m＝7﹣（﹣1）＝8；
当C是P、B中点时，
依题意有m﹣1＝7﹣（﹣1），
解得m＝9．
综上所述，m＝6或7或7.5或8或9．
25．我国著名数学家华罗庚说过“数缺形时少直观，形少数时难入微”．数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．
例如，式子的几何意义是数轴上所对应的点与2所对应的点之间的距离；因为，所以的几何意义就是数轴上所对应的点与-1所对应的点之间的距离．
结合数轴与绝对值的知识回答下列问题：
（1）若，则 ；的最小值是 ．
（2）若，则的值为 ；若，则的值为 ．
（3）是否存在使得取最小值，若存在，直接写出这个最小值及此时的取值情况；若不存在，请说明理由．
【答案】（1）5或-1；5；（2）或4；或；（3）的最小值为17，此时
【详解】解：（1）∵，
∴，
∴，
∴或；
设A点表示的数为-2，B点表示的数为3，P点表示的数为x，
∴表示的意义即为数轴上一点P到A的距离和到B的距离之和，
如图所示，当P在AB之间（包含A、B）时，；
当P在A点左侧时；
同理当P在B点右侧时；
∴的最小值为5，
故答案为：5或-1；5；
（2）设A点表示的数为-2，B点表示的数为3，P点表示的数为x，
由（1）可知当当P在AB之间（包含A、B）时，，当P在A点左侧时，当P在B点右侧时
∵，∴当P在A点左侧时即，∴；
同理当P在B点右侧时即，∴；
∴当时，或4；
当时，∵，∴，解得符合题意；
当时，∵，
∴，解得符合题意；
当时，∵，∴，解得不符合题意；
当时，∵，∴，解得不符合题意；
∴综上所述，当，或；
故答案为：或4；或；
（3）当时，∴，
当时，∴，
当时，∴，
当时
∴，∴此时
∴综上所述，的最小值为17，此时．
26．已知∠AOB和∠COD均为锐角，∠AOB＞∠COD，OP平分∠AOC，OQ平分∠BOD，将∠COD绕着点O逆时针旋转，使∠BOC=α（0≤α＜180°）
（1）若∠AOB=60°，∠COD=40°，
①当α=0°时，如图1，则∠POQ= ；
②当α=80°时，如图2，求∠POQ的度数；
③当α=130°时，如图3，请先补全图形，然后求出∠POQ的度数；
（2）若∠AOB=m°，∠COD=n°，m＞n，则∠POQ= ，（请用含m、n的代数式表示）．
【答案】（1）①50°；②50°；③130°；（2）m°+n°或180°-m°-n°
【详解】解：（1）①∵∠AOB=60°，∠COD=40°，OP平分∠AOC，OQ平分∠BOD，
∴∠BOP=∠AOB=30°，∠BOQ=∠COD=20°，
∴∠POQ=50°，
故答案为：50°；
②解：∵∠AOB=60°，∠BOC=α=80°，
∴∠AOC=140°，
∵OP平分∠AOC，
∴∠POC=∠AOC=70°，
∵∠COD=40°，∠BOC=α=80°，
且OQ平分∠BOD，
同理可求∠DOQ=60°，
∴∠COQ=∠DOQ-∠DOC=20°，
∴∠POQ=∠POC-∠COQ=70°-20°=50°；
③解：补全图形如图3所示，
∵∠AOB=60°，∠BOC=α=130°，
∴∠AOC=360°-60°-130°=170°，
∵OP平分∠AOC，
∴∠POC=∠AOC=85°，
∵∠COD=40°，∠BOC=α=130°，
且OQ平分∠BOD，
同理可求∠DOQ=85°，
∴∠COQ=∠DOQ-∠DOC=85°-40°=45°，
∴∠POQ=∠POC+∠COQ=85°+45°=130°；
（2）当∠AOB=m°，∠COD=n°时，如图2，
∴∠AOC= m°+ °，
∵OP平分∠AOC，
∴∠POC=(m°+ °)，
同理可求∠DOQ=(n°+ °)，
∴∠COQ=∠DOQ-∠DOC=(n°+ °)- n°=(-n°+ °)，
∴∠POQ=∠POC-∠COQ=(m°+ °)-(-n°+ °)
=m°+n°，
当∠AOB=m°，∠COD=n°时，如图3，
∵∠AOB=m°，∠BOC=α，
∴∠AOC=360°-m°-°，
∵OP平分∠AOC，
∴∠POC=∠AOC=180°(m°+ °)，
∵∠COD=n°，∠BOC=α，
且OQ平分∠BOD，
同理可求∠DOQ=(n°+ °)，
∴∠COQ=∠DOQ-∠DOC=(n°+ °)-n°=(-n°+ °)，
∴∠POQ=∠POC+∠COQ=180°(m°+ °)+(-n°+ °)
=180°-m°-n°，
综上所述，若∠AOB=m°，∠COD=n°，则∠POQ=m°+n°或180°-m°-n°．
故答案为：m°+n°或180°-m°-n°．