七年级下册5.2.2 平行线的判定示范课ppt课件

这是一份七年级下册5.2.2 平行线的判定示范课ppt课件，共20页。PPT课件主要包含了学习目标，解EFBC，理由如下，对顶角相等，等量代换，合作探究，练测促学，巩固新知，例题讲解，答AB∥CD等内容，欢迎下载使用。
1.进一步掌握平行线的判定方法，并会运用平行线的判定解决问题。2.掌握垂直于同一条直线的两条直线互相平行。3.经历例题的分析过程，从中体会转化的思想和分析问题的方法，进一步培养推理能力。
例1 如图，直线EF与∠ABC的一边BA相交于D， ∠B+∠ADE=180°，EF与BC平行吗？ 为什么？
∵ ∠B+ ∠1=180°（ ）,
∠1= ∠2（ ）,
∴ ∠B+ ∠2=180°（ ）.
∴ EF∥BC（ ）.
同旁内角互补，两直线平行
新知一 平行线判定方法的灵活应用
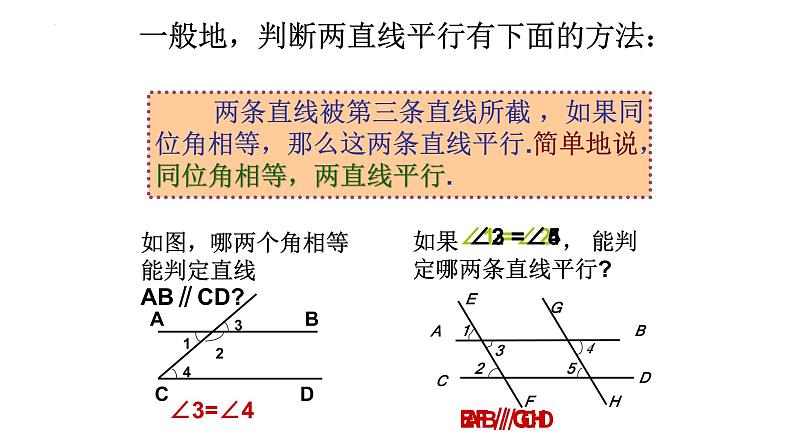
一般地，判断两直线平行有下面的方法：
两条直线被第三条直线所截 ，如果同位角相等，那么这两条直线平行.简单地说，同位角相等，两直线平行.
如图，哪两个角相等能判定直线AB∥CD?
如果 ， 能判定哪两条直线平行?
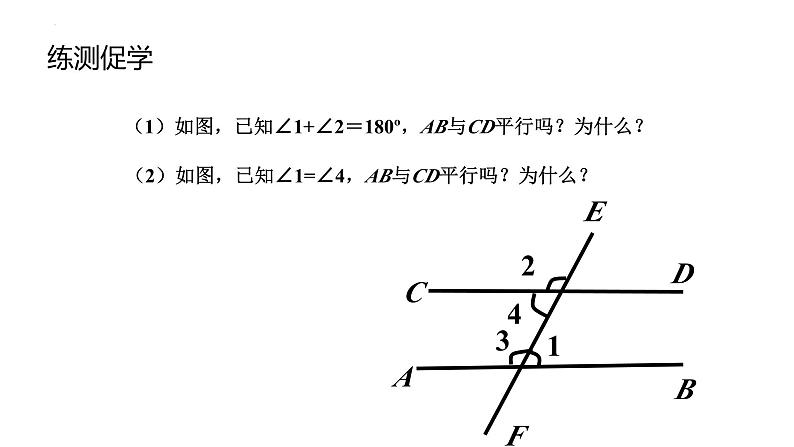
（1）如图，已知∠1+∠2＝180º，AB与CD平行吗？为什么？
（2）如图，已知∠1=∠4，AB与CD平行吗？为什么？
如图所示，直线a，b都与直线c相交，给出的下列条件：①∠1＝∠7；②∠3＝∠5；③∠1＋∠8＝180°；④∠3＝∠6.其中能判断a∥b的是( )A. ①③　 B. ②③C. ③④　 D. ①②③
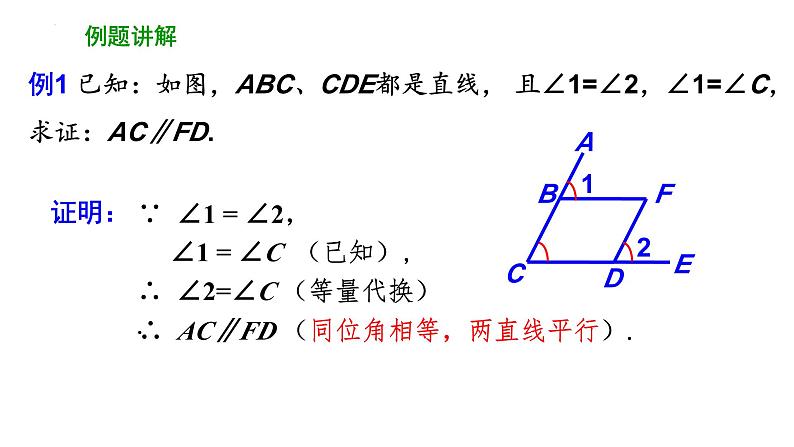
例1 已知：如图，ABC、CDE都是直线， 且∠1=∠2，∠1=∠C，求证：AC∥FD.
∵ ∠1 = ∠2， ∠1 = ∠C （已知）,
∴ ∠2=∠C （等量代换）.
∴ AC∥FD （同位角相等，两直线平行）.
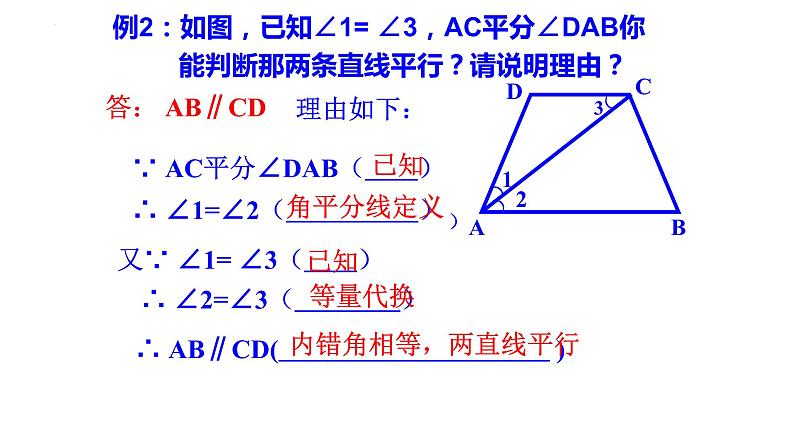
例2：如图，已知∠1= ∠3，AC平分∠DAB你 能判断那两条直线平行？请说明理由？

∵ AC平分∠DAB（ ）
∴ ∠1=∠2（ ）
又∵ ∠1= ∠3（ ）
∴ ∠2=∠3（ ）
∴ AB∥CD( )
内错角相等，两直线平行
如图,∠1＝∠2,则下列结论正确的是（ ）
A. AD//BC B. AB//CD C. AD//EF D. EF//BC
如图，∠1＝∠2，能判断AB∥DF吗？为什么？
答：添加∠CBD＝∠EDB
内错角相等，两直线平行.
若不能判断AB∥DF，你认为还需要再添加的一个条件是什么呢？写出这个条件，并说明你的理由.
解： AB∥CD .理由如下：∵ AC平分∠BAD，∴ ∠1=∠3 .∵∠1=∠2，∵ ∠2和∠3是内错角，∴ AB∥CD（内错角相等，两直线平行）.
例3 已知：如图，四边形ABCD中，AC平分∠BAD，∠1=∠2，AB与CD平行吗？为什么？
在同一平面内，两条直线垂直于同一条直线，这两条直线平行吗？为什么？
猜想：垂直于同一条直线的两条直线平行.
新知二 在同一平面内，垂直于同一直线的两直线平行
在同一平面内，b⊥a,c⊥a，试说明：b∥c.
∵b⊥a ，c ⊥a （已知）,
(同位角相等，两直线平行).
∴∠1= ∠2 = 90°
∵ b⊥a,c⊥a(已知),∴∠1=∠2=90°(垂直定义).∴b∥c(内错角相等，两直线平行).
当∠ABH= 时，AB∥DE当∠ABE 时，AB∥DE当∠HBC= 时，BC ∥EF当∠GBC= 时，BC ∥EF
2、如图，a∥c，∠1=∠2，那么c∥b吗？
解：∵ ∠1=∠2（ ）
∴ a∥b（ ）
∵ a∥c（ ）
∴ c∥b（ ）
3、如图,a、b、c、d是直线,E、F、G、H是交点,(1)若∠1=∠2,可以证明a∥b,而不能证明c∥d.这是因为∠1和∠2是直线_______和_____被直线____所截而成,它们与直线____无关. (2)同样的道理,若已知∠1 = ∠3,可以证明______∥______,这是因为它们是直线____和______被直线______所截而成.
4、如图，BC、DE分别平分ABD和BDF，且1=2， 请找出平行线，并说明理由。