

- 北师大版七年级数学下册尖子生培优必刷题 专题2.1两条直线的位置关系专项提升训练(重难点培优)(原卷版+解析 ) 试卷 0 次下载
- 北师大版七年级数学下册尖子生培优必刷题 专题2.2探索直线平行的条件专项提升训练(重难点培优)(原卷版+解析 ) 试卷 0 次下载
- 北师大版七年级数学下册尖子生培优必刷题 专题2.5平行线的性质与判定大题专练(填空型问题)(原卷版+解析 ) 试卷 0 次下载
- 北师大版七年级数学下册尖子生培优必刷题 专题2.6平行线的性质与判定大题专练(基础篇,重难点培优)(原卷版+解析 ) 试卷 0 次下载
- 北师大版七年级数学下册尖子生培优必刷题 专题2.7平行线的性质与判定大题专练(拔高篇,重难点培优)(原卷版+解析 ) 试卷 0 次下载
初中北师大版3 平行线的性质课堂检测
展开班级:___________________ 姓名:_________________ 得分:_______________
注意事项:
本试卷满分120分,试题共24题,其中选择10道、填空6道、解答8道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2022秋•碑林区校级月考)如图,a∥b.∠1=58°,则∠2的度数为( )
A.58°B.112°C.120°D.132°
2.(2023秋•蓝田县期末)如图,已知直线a∥b,若∠1=∠A,则∠A的度数为( )
A.70°B.60°C.50°D.40°
3.(2023秋•盐湖区校级期末)如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转( )
A.10°B.20°C.30°D.40°
4.(2022秋•桥西区期中)下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容.( )
A.※代表∠ABCB.⊙代表同旁内角
C.▲代表∠BFED.@代表同位角
5.(2022•陇县三模)如图,直线AB∥CD,直线EF分别交AB,CD于点G,H.GM平分∠BGH,且∠GHM=48°,那么∠GMD的度数为( )
A.96°B.104°C.114°D.124°
6.(2023秋•郓城县期末)如图,将一副直角三角板按图中所示位置摆放,保持两条斜边互相平行,则∠1=( )
A.15°B.20°C.25°D.30°
7.(2023秋•霍州市期末)如图,如果AB∥EF、EF∥CD,若∠1=50°,则∠2+∠3的和是( )
A.200°B.210°C.220°D.230°
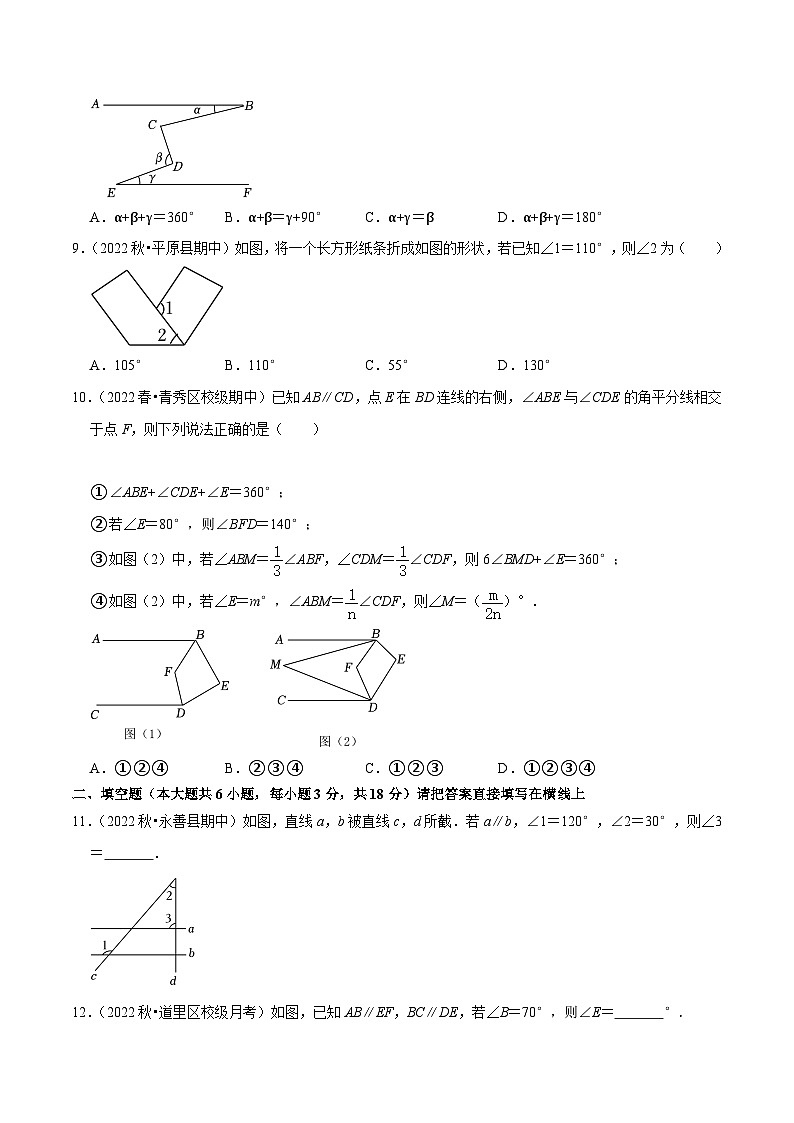
8.(2023秋•雅安期末)如图,AB∥EF,∠BCD=90°,探索图中角α,β,γ之间的关系式正确的是( )
A.α+β+γ=360°B.α+β=γ+90°C.α+γ=βD.α+β+γ=180°
9.(2022秋•平原县期中)如图,将一个长方形纸条折成如图的形状,若已知∠1=110°,则∠2为( )
A.105°B.110°C.55°D.130°
10.(2022春•青秀区校级期中)已知AB∥CD,点E在BD连线的右侧,∠ABE与∠CDE的角平分线相交于点F,则下列说法正确的是( )
①∠ABE+∠CDE+∠E=360°;
②若∠E=80°,则∠BFD=140°;
③如图(2)中,若∠ABM=∠ABF,∠CDM=∠CDF,则6∠BMD+∠E=360°;
④如图(2)中,若∠E=m°,∠ABM=∠CDF,则∠M=()°.
A.①②④B.②③④C.①②③D.①②③④
二、填空题(本大题共6小题,每小题3分,共18分)请把答案直接填写在横线上
11.(2022秋•永善县期中)如图,直线a,b被直线c,d所截.若a∥b,∠1=120°,∠2=30°,则∠3= .
12.(2022秋•道里区校级月考)如图,已知AB∥EF,BC∥DE,若∠B=70°,则∠E= °.
13.(2022春•海淀区校级月考)如图,一把长方形直尺沿直线断开并错位,点E,D,B,F在同一条直线上.若∠DBC=54°,则∠ADE的度数是 .
14.(2022秋•鼓楼区校级期中)已知三条线段AB,CD,EF满足:AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD的度数是 .
15.(2022•东胜区二模)如图,小刀的刀片上、下是平行的,刀柄外形是一个直角梯形(见图中标示),若∠1=65°,则∠2的度数是 .
16.(2022秋•道里区校级月考)如图,直线AB∥CD,点E、F分别为直线AB和CD上的点,点P为两条平行线间的一点,连接PE和PF,过点P作∠EPF的平分线交直线CD于点G,过点F作FH⊥PG,垂足为H,若∠DGP﹣∠PFH=120°,则∠AEP= °.
三、解答题(本大题共8小题,共72分.解答时应写出文字说明、证明过程或演算步骤)
17.(2022春•清镇市期中)如图,直线b,c被直线a所截,已知∠1+∠2=240°,b∥c,求∠2和∠3的度数.
18.(2022春•清镇市期中)如图,已知EF∥BC,AC平分∠BAF,∠B=50°,求∠BAC的度数.
19.(2022春•思明区校级期中)如图,AB∥CD,CE平分∠ACD,∠A=108°,求∠AEC的度数.
20.(2022春•宿豫区期中)如图,点B、C在直线AD上,∠DCG=70°,BF平分∠DBE,CG∥BF,求∠ABE的度数.
21.(2022春•岳麓区校级期末)如图,已知AB∥CD,点M是直线AB,CD内部一点,连接MB,MD.
(1)探究:①若∠B=25°,∠D=40°,则∠BMD= °;
②若∠B=α,∠D=β,则∠BMD= ;
(2)猜想:图中∠B,∠D与∠BMD之间的数量关系,并说明理由.
22.(2022春•山阳县期末)如图,已知AC∥FE,∠1+∠2=180°.
(1)求证:∠FAB=∠BDC;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
23.(2022春•龙岗区校级期中)如图,图①是一种网红弹弓的实物图,在两头上系上皮筋,拉动皮筋可形成平面示意图如图②和图③,弹弓的两边可看成是平行的,即AB∥CD,各活动小组探索∠APD与∠A,∠C之间数量关系时,有如下发现:
(1)在图②所示的图形中,若∠A=30°,∠D=35°,则∠APD= ;
(2)在图③中,若∠A=150°,∠APD=60°,则∠D= ;
(3)有同学在图②和图③的基础上,画出了图④所示的图形,其中AB∥CD,请判断∠α,∠β,∠γ之间的关系,并说明理由.
24.(2022春•天府新区月考)已知直线AB∥CD.直线EF分别与AB、CD交于点G、H,直线MS经过点G,与CD交于点P,且∠BGM=2∠EGM.
(1)如图1所示,当∠EGM=25°时,
①求∠GPH的度数;
②在直线MS上取一点O,使得∠GHO=10°,求∠GOH的度数.
(2)如图2所示,在射线GA上任取一点I,连接HI,∠IGP的角平分线GQ和∠IHC的角平分线HQ交于点Q,请写出∠GQH、∠QGH、∠GIH间的数量关系,并说明理由.
如图,AB∥EF,CB∥DE.求证:∠ADE+∠BFE=180°.
证明:
∵AB∥EF,∴∠ADE=※(两直线平行,⊙相等).
∵CB∥DE,∴∠DEF+▲=180°(两直线平行,@互补).
∴∠ADE+∠BFE=180°.
专题2.3平行线的性质专项提升训练(重难点培优)
班级:___________________ 姓名:_________________ 得分:_______________
注意事项:
本试卷满分120分,试题共24题,其中选择10道、填空6道、解答8道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2022秋•碑林区校级月考)如图,a∥b.∠1=58°,则∠2的度数为( )
A.58°B.112°C.120°D.132°
【分析】根据平行线性质得出∠1=∠3,根据对顶角相等即可得出答案.
【解答】解:如图,
∵a∥b,∠1=58°,
∴∠3=∠1=58°,
∴∠2=∠3=58°,
故选:A.
2.(2023秋•蓝田县期末)如图,已知直线a∥b,若∠1=∠A,则∠A的度数为( )
A.70°B.60°C.50°D.40°
【分析】由平行线的性质可得∠ADE=∠ABC=80°,再利用三角形的外角性质即可求解.
【解答】解:如图,
∵a∥b,
∴∠ADE=∠ABC=80°,
∵∠ADE=∠1+∠A,∠1=∠A,
∴2∠A=∠ADE,
即2∠A=80°,
解得∠A=40°.
故选:D.
3.(2023秋•盐湖区校级期末)如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转( )
A.10°B.20°C.30°D.40°
【分析】由平行线的判定“同位角相等,两直线平行”可知,∠EGB=∠EHD时,AB∥CD,即∠EGB需要变小20°,即将木棒AB绕点G逆时针旋转20°即可.
【解答】解:当∠EGB=∠EHD时,AB∥CD,
∵∠EGB=100°,∠EHD=80°,
∴∠EGB需要变小20°,即将木棒AB绕点G逆时针旋转20°.
故选:B.
4.(2022秋•桥西区期中)下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容.( )
A.※代表∠ABCB.⊙代表同旁内角
C.▲代表∠BFED.@代表同位角
【分析】先根据平行线的性质,得出∠ADE=∠DEF,∠DEF+∠BFE=180°,再求得∠ADE+∠BFE=180°即可.
【解答】证明:∵AB∥EF,
∴∠ADE=∠DEF (两直线平行,内错角相等).
∵CB∥DE,
∴∠DEF+∠BFE=180°(两直线平行,同旁内角互补).
∴∠ADE+∠BFE=180°.
故选:C.
5.(2022•陇县三模)如图,直线AB∥CD,直线EF分别交AB,CD于点G,H.GM平分∠BGH,且∠GHM=48°,那么∠GMD的度数为( )
A.96°B.104°C.114°D.124°
【分析】根据两直线平行,同旁内角互补求出∠BGH,再根据角平分线的定义可得∠BGM=∠BGH,然后根据两直线平行,同旁内角互补列式计算即可得解.
【解答】解:∵AB∥CD,∠GHM=48°,
∴∠BGH=180°﹣∠GHM=180°﹣48°=132°,
∵GM平分∠BGH,
∴∠BGM=∠BGH=×132°=66°,
∵AB∥CD,
∴∠GMD=180°﹣∠BGM=180°﹣66°=114°.
故选:C.
6.(2023秋•郓城县期末)如图,将一副直角三角板按图中所示位置摆放,保持两条斜边互相平行,则∠1=( )
A.15°B.20°C.25°D.30°
【分析】利用直角三角板值的特殊角,平行线的性质和三角形的内角和定理解答即可.
【解答】解:如图,
由题意得:∠B=45°,∠F=30°,∠DAC=90°,
∵BC∥DF,
∴∠EDA=∠B=45°,
∵∠EDF+∠F+∠DAF=180°,
∴∠DAF=105°,
∴∠1=∠DAF﹣∠DAC=105°﹣90°=15°,
故选:A.
7.(2023秋•霍州市期末)如图,如果AB∥EF、EF∥CD,若∠1=50°,则∠2+∠3的和是( )
A.200°B.210°C.220°D.230°
【分析】由平行线的性质可用∠2、∠3分别表示出∠BOE和∠COF,再由平角的定义可得出答案.
【解答】解:∵AB∥EF,
∴∠2+∠BOE=180°,
∴∠BOE=180°﹣∠2,同理可得∠COF=180°﹣∠3,
∵O在EF上,
∴∠BOE+∠1+∠COF=180°,
∴180°﹣∠2+∠1+180°﹣∠3=180°,
∴∠2+∠3=180°+∠1=180°+50°=230°,
故选:D.
8.(2023秋•雅安期末)如图,AB∥EF,∠BCD=90°,探索图中角α,β,γ之间的关系式正确的是( )
A.α+β+γ=360°B.α+β=γ+90°C.α+γ=βD.α+β+γ=180°
【分析】首先过点C作CM∥AB,过点D作DN∥AB,由AB∥EF,即可得AB∥CM∥DN∥EF,然后由两直线平行,内错角相等,即可求得答案.
【解答】解:过点C作CM∥AB,过点D作DN∥AB,
∵AB∥EF,
∴AB∥CM∥DN∥EF,
∴∠BCM=α,∠DCM=∠CDN,∠EDN=γ,
∵β=∠CDN+∠EDN=∠CDN+γ①,∠BCD=α+∠CDN=90°②,
由①②得:α+β﹣γ=90°.
故选:B.
9.(2022秋•平原县期中)如图,将一个长方形纸条折成如图的形状,若已知∠1=110°,则∠2为( )
A.105°B.110°C.55°D.130°
【分析】先根据两直线平行,同旁内角互补的性质求出∠3,再根据翻折的性质列式计算即可求出∠2.
【解答】解:如图,
∵纸条的两边互相平行,
∴∠1+∠3=180°,
∵∠1=110°,
∴∠3=180°﹣∠1=180°﹣110°=70°,
根据翻折的性质得,2∠2+∠3=180°,
∴∠2=(180°﹣∠3)=(180°﹣70°)=55°.
故选:C.
10.(2022春•青秀区校级期中)已知AB∥CD,点E在BD连线的右侧,∠ABE与∠CDE的角平分线相交于点F,则下列说法正确的是( )
①∠ABE+∠CDE+∠E=360°;
②若∠E=80°,则∠BFD=140°;
③如图(2)中,若∠ABM=∠ABF,∠CDM=∠CDF,则6∠BMD+∠E=360°;
④如图(2)中,若∠E=m°,∠ABM=∠CDF,则∠M=()°.
A.①②④B.②③④C.①②③D.①②③④
【分析】分别过E、F作GE∥AB,FH∥CD,再根据平行线的性质可以得到解答.
【解答】解:∵AB∥CD,
∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠BEG+∠CDE+∠DEG=360°,即∠ABE+∠BED+∠CDE=360°,①正确,
∵∠BED=80°,∠ABE+∠BED+∠CDE=360°,
∴∠ABE+∠CDE=280°,
∵AB∥CD,
∴∠ABF=∠BFH,∠CDF=∠DFH,
∴∠BFD=∠BFH+∠DFH=∠ABF+∠CDF=(∠ABE+∠CDE)=140°,②正确,
与上同理,∠BMD=∠ABM+∠CDM=(∠ABF+∠CDF),
∴6∠BMD=2(∠ABF+∠CDF)=∠ABE+∠CDE,
∴6∠BMD+∠E=360°,③正确,
由题意,④不一定正确,
∴①②③正确,
故选:C.
二、填空题(本大题共6小题,每小题3分,共18分)请把答案直接填写在横线上
11.(2022秋•永善县期中)如图,直线a,b被直线c,d所截.若a∥b,∠1=120°,∠2=30°,则∠3= 90° .
【分析】由平行线的性质可得∠ABC=∠1=120°,再由三角形的外角性质可求得∠3的度数.
【解答】解:如图,
∵a∥b,∠1=120°,
∴∠ABC=∠1=120°,
∵∠2=30°,
∴∠3=∠ABC﹣∠2=120°﹣30=90°.
故答案为:90°.
12.(2022秋•道里区校级月考)如图,已知AB∥EF,BC∥DE,若∠B=70°,则∠E= 110 °.
【分析】先根据AB∥EF求出∠1的度数,再由BC∥DE即可得出∠E的度数.
【解答】解:∵AB∥EF,∠B=70°,
∴∠1=180°﹣70°=110°.
∵BC∥DE,
∴∠E=∠1=110°.
故答案为:110.
13.(2022春•海淀区校级月考)如图,一把长方形直尺沿直线断开并错位,点E,D,B,F在同一条直线上.若∠DBC=54°,则∠ADE的度数是 126° .
【分析】先根据平行线的性质得出∠ADF=∠DBC=54°,再由补角的定义即可得出结论.
【解答】解:∵直尺的两边互相平行,
∴∠ADF=∠DBC=54°,
∴∠ADE=180°﹣54°=126°.
故答案为:126°.
14.(2022秋•鼓楼区校级期中)已知三条线段AB,CD,EF满足:AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD的度数是 140° .
【分析】如图,作辅助线;首先运用平行线的性质求出∠DGC的度数,借助三角形外角的性质求出∠ACD即可解决问题.
【解答】解:如图,延长AC交EF于点G,
∵AB∥EF,∠BAC=50°,
∴∠DGC=∠BAC=50°,
∵CD⊥EF,
∴∠CDG=90°,
∴∠ACD=90°+50°=140°.
故答案为:140°.
15.(2022•东胜区二模)如图,小刀的刀片上、下是平行的,刀柄外形是一个直角梯形(见图中标示),若∠1=65°,则∠2的度数是 25° .
【分析】延长BE交CD于F,由AB∥CD知∠1+∠BFC=180°,据此得出∠BFC=110°,根据∠BED=∠DEF=90°,∠BFC=∠2+∠DEF可得答案.
【解答】解:如图,延长BE交CD于F,
∵AB∥CD,
∴∠1+∠BFC=180°,
∵∠1=65°,
∴∠BFC=115°,
∵∠BED=∠DEF=90°,∠BFC=∠2+∠DEF,
∴∠2=∠BFC﹣∠DEF=115°﹣90°=25°,
故答案为:25°.
16.(2022秋•道里区校级月考)如图,直线AB∥CD,点E、F分别为直线AB和CD上的点,点P为两条平行线间的一点,连接PE和PF,过点P作∠EPF的平分线交直线CD于点G,过点F作FH⊥PG,垂足为H,若∠DGP﹣∠PFH=120°,则∠AEP= 30 °.
【分析】过点P作PQ∥AB,则PQ∥AB∥CD,根据平行线的性质与角平分线定义得∠AEP=2∠FPG﹣∠CFP,再根据三角形的外角定理,结合已知条件∠DGP﹣∠PFH=120°,得∠HFG=120°﹣∠FPG,由FH⊥PG,根据三角形内角和定理得∠PFH=90°﹣∠FPG,由平角定义得∠CFP=2∠PFG﹣30°,进而便可求得结果.
【解答】解:过点P作PQ∥AB,则PQ∥AB∥CD,
∴∠AEP=∠EPQ,∠CFP=∠FPQ,
∴∠AEP+∠CFP=∠EPQ+∠FPQ=∠EPF,
∵PD平分∠EPF,
∴∠EPF=2∠FPG,
∴∠AEP=2∠FPG﹣∠CFP,
∵∠DGP﹣∠PFH=120°,∠DGP=∠FPG+∠PFH+∠HFG,
∴∠HFG=120°﹣∠FPG,
∵FH⊥PG,
∴∠PFH=90°﹣∠FPG,
∴∠CFP=180°﹣∠PFH﹣∠HFG=2∠PFG﹣30°,
∴∠AEP=2∠FPG﹣∠CFP=30°,
故答案为:30.
三、解答题(本大题共8小题,共72分.解答时应写出文字说明、证明过程或演算步骤)
17.(2022春•清镇市期中)如图,直线b,c被直线a所截,已知∠1+∠2=240°,b∥c,求∠2和∠3的度数.
【分析】由对顶角相等知∠1=∠2,再根据∠1+∠2=240°可求出∠2,然后由平行线的性质可求∠3.
【解答】解:∵∠1=∠2(对顶角相等),
∠1+∠2=240°,
∴∠1=∠2=120°.
∵b∥c,
∴∠2+∠3=180°(两直线平行,同旁内角互补).
∴∠3=60°.
18.(2022春•清镇市期中)如图,已知EF∥BC,AC平分∠BAF,∠B=50°,求∠BAC的度数.
【分析】根据EF∥BC可知∠B+∠BAF=180°,求出∠BAF,再根据AC平分∠BAF即可求出∠BAC.
【解答】解:∵EF∥BC,
∴∠B+∠BAF=180°(两直线平行,同旁内角互补),
∴∠BAF=180°﹣∠B=180°﹣50°=130°.
∵AC平分∠BAF,
∴∠BAC=∠BAF=65°.
19.(2022春•思明区校级期中)如图,AB∥CD,CE平分∠ACD,∠A=108°,求∠AEC的度数.
【分析】先由AB∥CD,∠A=108°,得∠ACD的度数,再根据CE平分∠ACD,可得∠DCE的度数,再根据两直线平行,内错角相等求出结论.
【解答】解:∵AB∥CD,
∴∠A+∠ACD=180°,
∵∠A=108°,
∴∠ACD=180°﹣∠A=180°﹣108°=72°,
∵CE平分∠ACD,
∴∠ACE=∠DCE=36°,
∵AB∥CD,
∴∠AEC=∠DCE=36°.
20.(2022春•宿豫区期中)如图,点B、C在直线AD上,∠DCG=70°,BF平分∠DBE,CG∥BF,求∠ABE的度数.
【分析】根据CG∥BF,可证得∠DCG=∠CBF,根据BF平分∠DBE,可证得∠CBE=2∠CBF,根据邻补角的定义求出∠ABE即可.
【解答】解:∵CG∥BF,
∴∠DCG=∠CBF,
∵∠DCG=70°,
∴∠DCG=∠CBF=70°,
∵BF平分∠DBE,
∴∠CBE=2∠CBF=140°,
∴∠ABE=180°﹣∠CBE=180°﹣140°=40°.
21.(2022春•岳麓区校级期末)如图,已知AB∥CD,点M是直线AB,CD内部一点,连接MB,MD.
(1)探究:①若∠B=25°,∠D=40°,则∠BMD= 65 °;
②若∠B=α,∠D=β,则∠BMD= α+β ;
(2)猜想:图中∠B,∠D与∠BMD之间的数量关系,并说明理由.
【分析】(1)过M点作MN∥AB即可.得到∠BMD=∠B+∠D.
(2)运用(1)的结论.
(3)运用(1)的结论.
【解答】解:(1)如图,过M点作MN∥AB,
∴MN∥AB∥CD,
∴∠BMN=∠B,∠DMN=∠D,
∴∠BMD=∠BMN+∠DMN=∠B+∠D=25°+40°=65°,
故答案为:65.
(2)同理,∠B=α,∠D=β,
∴∠BMD=∠B+∠D=α+β,
故答案为:α+β.
(3)同理,∠BMD=∠B+∠D.
22.(2022春•山阳县期末)如图,已知AC∥FE,∠1+∠2=180°.
(1)求证:∠FAB=∠BDC;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
【分析】(1)根据AC∥EF,证得∠1+∠FAC=180°,已知∠1+∠2=180°,等量代换∠2=∠FAC,从而证得FA∥CD,得出∠FAB=∠BDC;
(2)根据角平分线的定义得∠FAC=∠CAD,∠FAD=2∠FAC,得出∠FAD=2∠2,根据已知求出∠2的度数,根据EF⊥BE,AC∥EF,证得AC⊥BE,得出∠ACB=90°,进一步求出∠BCD的度数.
【解答】(1)证明:∵AC∥EF,
∴∠1+∠FAC=180°,
∵∠1+∠2=180°,
∴∠2=∠FAC,
∴FA∥CD,
∴∠FAB=∠BDC;
(2)解:∵AC平分∠FAD,
∴∠FAC=∠CAD,∠FAD=2∠FAC,
由(1)知∠2=∠FAC,
∴∠FAD=2∠2,
∴∠2=∠FAD,
∵∠FAD=80°,
∴∠2=×80°=40°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠2=50°.
23.(2022春•龙岗区校级期中)如图,图①是一种网红弹弓的实物图,在两头上系上皮筋,拉动皮筋可形成平面示意图如图②和图③,弹弓的两边可看成是平行的,即AB∥CD,各活动小组探索∠APD与∠A,∠C之间数量关系时,有如下发现:
(1)在图②所示的图形中,若∠A=30°,∠D=35°,则∠APD= 65° ;
(2)在图③中,若∠A=150°,∠APD=60°,则∠D= 150° ;
(3)有同学在图②和图③的基础上,画出了图④所示的图形,其中AB∥CD,请判断∠α,∠β,∠γ之间的关系,并说明理由.
【分析】(1)过点P作PQ∥AB,根据AB∥CD,证得PQ∥AB∥CD,进而根据平行线的性质得到∠APD=∠A+∠D即可解答;
(2)过点P作PQ∥AB,根据AB∥CD,证得PQ∥AB∥CD,进而得到∠A+∠APQ=180°,∠D+∠DPQ=180°,求出∠DPQ=30°,进一步求出∠D即可;
(3)过点P作PQ∥AB,根据AB∥CD,证得PQ∥AB∥CD,根据平行线的性质得到α+∠BPQ=180°,γ=∠DPQ,进而得出β=∠BPQ+γ,进一步求出α+β﹣γ=180°.
【解答】解:(1)过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠A=∠APQ,∠D=∠DPQ,
∵∠A=30°,∠D=35°,
∴∠APD=∠APQ+∠DPQ=∠A+∠D=30°+35°=65°.
故答案为:65°;
(2)过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠A+∠APQ=180°,∠D+∠DPQ=180°,
∵∠A=150°,
∴∠APQ=30°,
∵∠APD=60°,
∴∠DPQ=30°,
∴∠D=180°﹣∠DPQ=180°﹣30°=150°.
故答案为:150°;
(3)过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴α+∠BPQ=180°,γ=∠DPQ,
∴∠BPQ=180°﹣α,
∵β=∠BPQ+∠DPQ,
∴β=∠BPQ+γ,
∴β=180°﹣α+γ,
即α+β﹣γ=180°.
24.(2022春•天府新区月考)已知直线AB∥CD.直线EF分别与AB、CD交于点G、H,直线MS经过点G,与CD交于点P,且∠BGM=2∠EGM.
(1)如图1所示,当∠EGM=25°时,
①求∠GPH的度数;
②在直线MS上取一点O,使得∠GHO=10°,求∠GOH的度数.
(2)如图2所示,在射线GA上任取一点I,连接HI,∠IGP的角平分线GQ和∠IHC的角平分线HQ交于点Q,请写出∠GQH、∠QGH、∠GIH间的数量关系,并说明理由.
【分析】(1)①运用平行线性质即可求得答案;
②如图1,过点O作ON∥AB,则∠MON=∠BOM=50°,由AB∥CD,可得∠EHD=∠BGE=75°,再由ON∥CD,可得∠NOH=95°,即可得出答案;
(2)如图2,过点Q作QN∥AB,则∠GQN=∠AGQ,利用角平分线定义可得:∠AGQ=∠QGP=∠AGP=∠QGH,∠QHC=∠IHC=∠GIH,即可得出答案.
【解答】解:(1)①∠BGM=2∠EGM,∠EGM=25°,
∴∠BGM=2×25°=50°,
∵AB∥CD,
∴∠GPH=∠BGM=50°;
②如图1,过点O作ON∥AB,
则∠MON=∠BOM=50°,
∵∠BGE=∠BGM+∠EGM=50°+25°=75°,AB∥CD,
∴∠EHD=∠BGE=75°,
∴∠DHO=∠EHD+∠GHO=75°+10°=85°,
∵AB∥CD,ON∥AB,
∴ON∥CD,
∴∠NOH=180°﹣∠DHO=180°﹣85°=95°,
∴∠GOH=∠MON+∠NOH=50°+95°=145°;
(2)2∠GQH=∠QGH+∠GIH.理由如下:
如图2,过点Q作QN∥AB,
则∠GQN=∠AGQ,
∵∠BGM=2∠EGM,∠BGM=∠AGP,∠EGM=∠FGP,
∴∠AGS=2∠FGS,
∵GQ平分∠AGP,
∴∠AGQ=∠QGP=∠AGP=∠QGH,
∵AB∥CD,
∴∠GIH=∠IHC,
∵HQ平分∠IHC,
∴∠QHC=∠IHC=∠GIH,
∵QN∥AB,AB∥CD,
∴QN∥CD,
∴∠NQH=∠QHC,
∴∠GQH=∠AGQ+∠QHC=∠QGH+∠GIH,
∴2∠GQH=∠QGH+∠GIH.
如图,AB∥EF,CB∥DE.求证:∠ADE+∠BFE=180°.
证明:
∵AB∥EF,∴∠ADE=※(两直线平行,⊙相等).
∵CB∥DE,∴∠DEF+▲=180°(两直线平行,@互补).
∴∠ADE+∠BFE=180°.
初中数学人教版七年级下册10.1 统计调查课时训练: 这是一份初中数学人教版七年级下册<a href="/sx/tb_c42629_t7/?tag_id=28" target="_blank">10.1 统计调查课时训练</a>,共17页。试卷主要包含了1统计调查专项提升训练,4,,5%,等内容,欢迎下载使用。
数学七年级下册7 整式的除法同步达标检测题: 这是一份数学七年级下册<a href="/sx/tb_c9971_t7/?tag_id=28" target="_blank">7 整式的除法同步达标检测题</a>,共17页。试卷主要包含了7整式的除法专项提升训练,14﹣π)0.等内容,欢迎下载使用。
初中北师大版6 完全平方公式测试题: 这是一份初中北师大版<a href="/sx/tb_c9970_t7/?tag_id=28" target="_blank">6 完全平方公式测试题</a>,共16页。试卷主要包含了6完全平方公式专项提升训练,75,求x﹣y;等内容,欢迎下载使用。













