初中数学湘教版七年级下册3.1 多项式的因式分解备课课件ppt

这是一份初中数学湘教版七年级下册3.1 多项式的因式分解备课课件ppt，共24页。

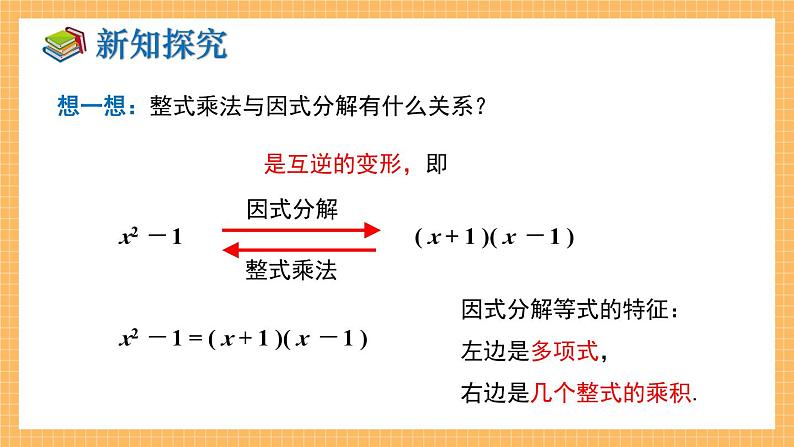
3.1 多项式的因式分解1.使学生了解因式分解的意义，理解因式分解的概念；通过对分解因式与整式的乘法的观察与比较，学习代数式的变形和转化与化归的能力，培养学生的分析问题能力与综合应用能力.2.认识因式分解与整式乘法的相互关系——互逆关系(即相反变形)，并能运用这种关系寻求因式分解的方法；通过解决实际问题，学会将实际应用问题转化为用所学到的数学知识解决问题，体验解决问题策略的多样性，发展实践应用意识.3.培养学生接受矛盾的对立统一观点，独立思考，勇于探索的精神和实事求是的科学态度.【教学重点】因式分解的概念.【教学难点】难点是理解因式分解与整式乘法的相互关系，并运用它们之间的相互关系寻求因式分解的方法.1.多项式的乘法有几种形式？单项式乘以多项式：a(m+n)=am+an多项式乘以多项式：(a+b)(m+n)=am+an+bm+bn2.乘法公式有哪些？讨论（1）21等于3乘那个数？（2）x2-1等于x+1乘哪个多项式？21=3×7.因为( x+1 )( x-1 )=x2-1，所以x2-1=( x+1 )( x-1 ).对于整数21于3，有整数7使得21=3×7，我们把3叫做21的一个因数，同理7也是21的一个因数. 类似地，对于多项式x2-1与x+1，由整式的乘法有多项式x-1使得x2-1=( x+1 )( x-1 )成立，我们把多项式x+1叫做x2-1的一个因式.同理，x-1也是x2-1的一个因式.定义： 把一个多项式化为几个整式的乘积的形式，像这样的式子变形叫做把这个多项式因式分解(也叫做把这个多项式分解因式). 一般地，对于两个多项式 f 与 g，如果有多项式 h 使得 f = gh，那么我们把 g 叫做 f 的一个因式，此时，h 也是 f 的一个因式．单项式可看作只有一项的多项式↗因式分解的特点： 分解的结果一定是积的形式. 每个因式必须是整式. 因式要分解到不能分解为止.x2 － 1 ( x + 1 )( x － 1 )因式分解整式乘法x2 － 1 = ( x + 1 )( x － 1 )因式分解等式的特征：左边是多项式，右边是几个整式的乘积.想一想：整式乘法与因式分解有什么关系？是互逆的变形，即【例1】下列各式由左边到右边的变形，哪些是因式分解，哪些不是，为什么？ (1) a2+2ab + b2= (a+b)2; (2) m2+m-4=( m +3 ) ( m-2 )+2.是.因为从左边到右边是把多项式a2+2ab + b2表示成了多项式a+b与a+b的积的形式.不是.因为( m +3 ) ( m-2 )+2不是几个多项式乘积的形式.方法总结：因式分解与整式乘法是相反方向的变形，即互逆运算，二者是一个式子的不同表现形式．因式分解的右边是两个或几个整式的积的形式，整式乘法的右边是多项式的形式．1、下列从左到右的变形中是因式分解的有 (　　)① x2 － y2 － 1 ＝ (x ＋ y)( x － y) － 1；② x3 ＋ x ＝ x (x2 ＋ 1)；③ (x － y)2 ＝ x2 － 2xy ＋ y2；④ x2 － 9y2 ＝ (x ＋ 3y)(x － 3y)．A．1 个 B．2 个 C．3 个 D．4 个B【例2】检验下列因式分解是否正确.（1）x2+xy=x( x+y )；（2）a2-5a+6=(a-2)(a-3)；（3）2m2-n2=( 2m-n )( 2m+n ).解：（1）因为x( x+y )=x2+xy，所以（1）正确； （2）因为( a-2 )( a-3 )=a2-5a+6，所以（2）正确； （3）因为( 2m-n )( 2m+n )=4m2-n2≠2m2-n2，所以（3）不正确. x2 + x = x2(1 + )2、在下列等式中，从左到右的变形是因式分解的有 ；不是因式分解的，请说明为什么. ① ② ③④ ⑤ ⑥ ③⑥am + bm + c = m(a + b) + c24x2y = 3x ·8xyx2－ 1 = (x + 1)(x－ 1)(2x + 1)2 = 4x2 + 4x + 12x + 4y + 6z = 2(x + 2y + 3z)最后不是积的运算因式分解的对象是多项式是整式乘法每个因式必须是整式3、若多项式 x2 + ax + b 分解因式的结果为 a( x﹣2 )( x + 3 )，求 a，b 的值.解：因为 x2 + ax + b = a( x﹣2 )( x + 3 )， 即 x2 + ax + b = ax2 + ax﹣6a， 所以 a = 1，b =﹣6a =﹣6，方法归纳：对于此类问题，掌握因式分解与整式乘法为互逆运算是解题关键，应先把分解因式后的结果乘开，再与多项式的各项系数对应比较，使其分别相等即可.1.下列等式从左到右的变形，属于因式分解的是( ) A.a(m-n)＝am-an B.y2+2y+1＝y(y+2)+1 C.(x+3)(x+6)＝x2+9x+18 D.b3-b＝b(b+1)(b-1)D2. (7x-y)(7x+y)是下列哪一个多项式因式分解的结果( ) A.49x2+y2 B.-49x2+y2 C.49x2-y2 D.-49x2-y2C3. 根据整式乘法的经验把下列多项式因式分解： 4. 求 4，6，14 的最大公因数.4 = 1×2×2，6 = 1×2×3，14 = 1×2×7，最大公因数是 2. 解： 6. 甲、乙两个同学分解因式 x2 + ax + b 时，甲看错了 b，分解结果为 ( x + 2 )( x + 4 )；乙看错了 a，分解结果为( x + 1)( x + 9 )，求 a + b 的值.解：分解因式甲看错了 b，但 a 是正确的， 其分解结果为 x2 + ax + b = (x + 2)(x + 4) = x2 + 6x + 8， 所以 a = 6. 同理，乙看错了 a，但 b 是正确的， 分解结果为 x2 + ax + b = (x + 1)(x + 9) = x2 + 10x + 9， 所以 b = 9. 因此 a + b = 15.7、若多项式 x4 + mx3 + nx﹣16 含有因式 (x﹣2) 和 (x﹣1)， 求 mn 的值.解：因为 x4 + mx3 + nx﹣16 的最高次数是 4，所以可设 x4 + mx3 + nx﹣16 = (x﹣1)(x﹣2)(x2 + ax + b).则 x4 + mx3 + nx﹣16= x4 + (a﹣3)x3 + (b﹣3a + 2)x2 + (2a﹣3b)x + 2b.比较系数得 a﹣3 = m，b﹣3a + 2 = 0，2a﹣3b = n，2b =﹣16. 解得 b =﹣8，a =﹣2，m =﹣5，n = 20. 所以 mn =﹣5×20 =﹣100． 一般地，把一个多项式表示成若干个多项式的乘积的形式，称为把这个多项式因式分解. 一般地，对于两个多项式f与g，如果有多项式h使得f=gh，那么我们把g叫做f的一个因式.此时，h也是f的一个因式.f=gh因式分解要注意以下几点： 3. 要分解到不能分解为止.2. 分解的结果一定是几个整式的乘积的形式；1. 分解的对象必须是多项式；因式分解与整式乘法是互逆的过程.1. 习题3.1中第2、3、4题.2.完成同步练习册中本课时的练习.