








初中数学湘教版七年级下册3.1 多项式的因式分解优秀ppt课件
展开1.掌握因式分解的意义,会判断一个变形是不是因式分解.(重点)2.理解因式分解与整式乘法之间的联系与区别.(难点)
(1)21等于3乘哪个整数?
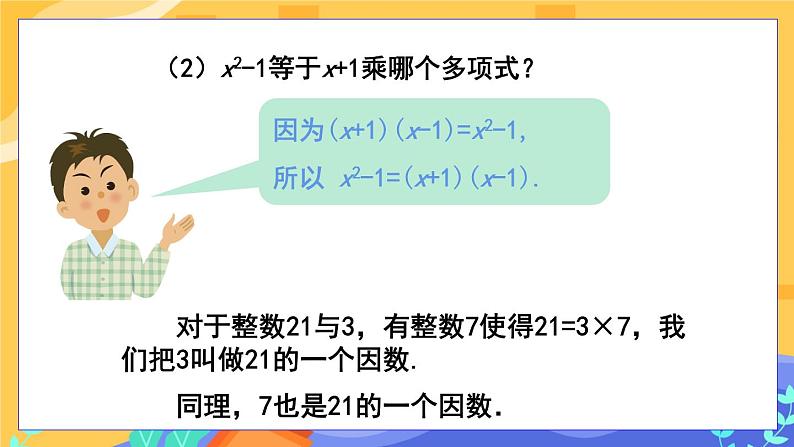
(2)x2-1等于x+1乘哪个多项式?
因为(x+1)(x-1)=x2-1,所以 x2-1=(x+1)(x-1).
对于整数21与3,有整数7使得21=3×7,我们把3叫做21的一个因数.
同理,7也是21的一个因数.
类似地,对于多项式x2-1与x+1,有整式的乘法有多项式x-1使得x2-1=(x+1)(x-1)成立,我们把多项式x+1叫做x2-1的一个因式.
同理,x-1也是x2-1的一个因式.
一般地,对于两个多项式f与g,如果有多项式h使得f=gh,那么我们把g叫做f的一个因式.
此时,h也是f的一个因式.
把x2-1写成(x+1)(x-1)的形式叫做把这个多项式因式分解.
一般地,把一个多项式表示成若干个多项式的乘积的形式,称为把这个多项式因式分解.
x2-1=(x+1)(x-1)
温馨提示:因式分解要注意以下几点:1.分解的对象必须是多项式.2.分解的结果一定是积的形式.3.结果中的每一个因式都必须是整式.
为什么要把一个多项式因式分解呢?
每一个大于1的正整数都能表示成若干个素(质)数的乘积的形式.
12 = 2×2×3, ①30 = 2×3×5 . ②
有了①式和②式,就容易求出12和30的最大公因数为
同样地,每一个多项式可以表示成若干个最基本的多项式的乘积的形式,从而为许多问题的解决架起了桥梁.
例如,以后我们要学习的分式的约分,解一元二次方程等,常常需要把多项式进行因式分解.
例1 下列各式由左边到右边的变形,哪些是因式分解,哪些不是,为什么?
(1) a2 + 2ab + b2 = (a+b)2;(2) m2 + m - 4 = (m+3)(m-2)+ 2 .
解:(1)是. 因为从左边到右边是把多项式a2+2ab+b2表示成了多项式a+b与a+b 的积的形式.
(2)不是. 因为(m+3)( m-2)+2不是几个多项式乘积的形式.
例2 检验下列因式分解是否正确. (1) x2 + xy = x(x+y) ; (2) a2 - 5a + 6 = (a-2)(a-3) ; (3) 2m2 -n2 = (2m-n)(2m+n) .
分析:检验因式分解是否正确,只要看等式右边的几个多项式的乘积与左边的多项式是否相等.
(2)因为(a-2)(a-3) = a2-5a+6, 所以因式分解a2 - 5a + 6 = (a-2)(a-3)正确.
解:(1)因为x( x + y ) = x2 + xy , 所以因式分解 x2 + xy = x(x + y)正确.
(3)因为(2m-n)(2m+n)= 4m2-n2≠2m2-n2, 所以因式分解2m2-n2=(2m-n)(2m+n)不正确.
根据左面算式填空:(1) 3x2-3x=_________(2)ma+mb+mc=___________(3) m2-16=__________(4) x2-6x+9=________ (5) a3-a=___________
计算下列各式:(1) 3x(x-1)= ,(2) m(a+b+c) = ,(3)(m+4)(m-4)= ,(4)(x-3)2= ,(5)a(a+1)(a-1)= ,
a(a+1)(a-1)
因式分解与整式乘法的关系
想一想:由a(a+1)(a-1)得到a3-a的变形是什么运算? 由a3-a得到a(a+1)(a-1)的变形与它有什么不同?
由a(a+1)(a-1)得到a3-a的变形是整式乘法,由a3-a得到a(a+1)(a-1)的变形与上面的变形互为逆过程.
x2-1 (x+1)(x-1)
x2-1 = (x+1)(x-1)
因式分解的特征:左边是多项式,右边是几个多项式的乘积
整式乘法与因式分解有什么关系?
例3 若多项式x2+ax+b分解因式的结果为a(x﹣2)(x+3),求a,b的值.
解:∵x2+ax+b=a(x﹣2)(x+3) =ax2+ax-6a. ∴a=1,b=﹣6a=﹣6.
方法归纳:对于此类问题,掌握因式分解与整式乘法为互逆运算是解题关键,应先把分解因式后的结果乘开,再与多项式的各项系数对应比较即可.
1.选择: (1)下列各式由左到右的变形是因式分解的是 ( ) A.-9+a2=-(3+a)(3-a) B.(x-2)(x-3)=x2-5x+6 C.a2-2ab+b2+a=(a-b)2+a D.m2+m=m2(1+ )
(2)(m+2n)(m-2n)是下列哪个多项式分解因式的结果( ) A.m2+4n2 B.-m2+4n2 C.m2-4n2 D.-m2-4n2
(3)下列多项式中,分解因式的结果为-(x+y)(x-y)的是( )A.x2﹣y2 B.﹣x2+y2C.x2+y2 D.﹣x2﹣y2
2.判断下列各式从左到右的变形中,是否为因式分解:
A. x(a﹣b)=ax﹣bx B. x2﹣1+y2=(x﹣1)(x+1)+y2 C. y2﹣1=(y+1)(y﹣1) D. ax+by+c=x(a+b)+c E. 2a3b=a2•2ab F. (x+3)(x﹣3)=x2﹣9
提示:判定一个变形是因式分解的条件:(1)左边是多项式.(2)右边是积的形式. (3)右边的因式全是整式.
3.填空: (2)根据下图写出一个因式分解的算式为_______________.
(1)对于(a-b)(x-y)=ax-ay-bx+by从左到右的变形是 ,从右到左的变是 ;
mn+m2=m(m+n)
4. 求4,6,20 的最大公因数.
解:因为4=2×2, 6=2×3, 20=2×2×5,
5.求代数式IR1+IR2+IR3的值,其中R1=19.2,R2=32.4,R3=38.4,I=2.5.
解: IR1+IR2+IR3 =I(R1+R2+R3) =2.5×(19.2+32.4+38.4) =2.5×90 =225.
定义:一般地,把一个多项式表示成若干个多项式的_____的形式,称为把这个多项式因式分解,也可称为___________.
与多项式乘法运算的关系
的变形过程.
前者是把一个多项式表示整式的_____,后者是把整式的______化为一个_________.
初中数学湘教版七年级下册3.1 多项式的因式分解精品习题ppt课件: 这是一份初中数学湘教版七年级下册3.1 多项式的因式分解精品习题ppt课件,文件包含31多项式的因式分解课件pptx、31多项式的因式分解练习pptx、31多项式的因式分解教案doc等3份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
湘教版3.1 多项式的因式分解完美版习题ppt课件: 这是一份湘教版3.1 多项式的因式分解完美版习题ppt课件,文件包含31多项式的因式分解课件pptx、31多项式的因式分解练习pptx、31多项式的因式分解教案doc等3份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
初中数学3.1 多项式的因式分解教案配套课件ppt: 这是一份初中数学3.1 多项式的因式分解教案配套课件ppt,文件包含31多项式的因式分解pptx、31多项式的因式分解docx、31多项式的因式分解练习doc等3份课件配套教学资源,其中PPT共11页, 欢迎下载使用。













