5.2 平行线及其判定 第3课时 初中数学人教版七年级下册上课课件

这是一份5.2 平行线及其判定 第3课时 初中数学人教版七年级下册上课课件，共28页。

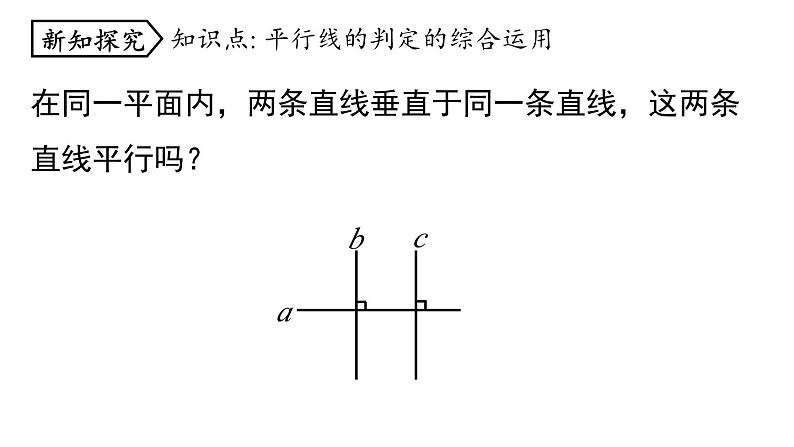
平行线及其判定七年级下册 RJ初中数学5.2.3相交线与平行线定义法.同位角相等，两直线平行.内错角相等，两直线平行.同旁内角互补，两直线平行.知识回顾进一步掌握平行线的判定方法，并会运用平行线的判定解决问题.学习目标在铺设铁轨时，两条直轨必须是互相平行的.课堂导入在同一平面内，两条直线垂直于同一条直线，这两条直线平行吗？知识点: 平行线的判定的综合运用新知探究例1在同一平面内，b⊥a，c⊥a，证明：b//c.12∵b⊥a ，c⊥a，(已知)证明：（方法一）如图，例1在同一平面内，b⊥a，c⊥a，证明：b//c.12∵b⊥a ，c⊥a，(已知)证明： （方法二）如图，例1在同一平面内，b⊥a，c⊥a，证明：b//c.12∵b⊥a ，c ⊥a，(已知)证明： （方法三）如图，∴∠1 + ∠2 = 180°， 例2如图，E 是 AB 上一点，F 是 DC 上一点，G 是 BC 延长线上一点.(1)如果∠B=∠DCG，可以判定哪两条直线平行？为什么？解：(1) AB//CD，同位角相等，两直线平行.例2如图，E 是 AB 上一点，F 是 DC 上一点，G 是 BC 延长线上一点.(2)如果∠D=∠DCG，可以判定哪两条直线平行？ 为什么？解：(2) AD//BC，内错角相等，两直线平行.例2如图，E 是 AB 上一点，F 是 DC 上一点，G 是 BC 延长线上一点.(3)如果∠D+∠DFE=180°，可以判定哪两条直线平行？为什么？解：(3) AD//EF，同旁内角互补，两直线平行.例3如图，已知 ∠1=75° ，∠2 =105°. AB 与 CD 平行吗？为什么？解：AB//CD，理由如下：∵ ∠1+∠3=180°，(邻补角互补)∠1=75°，(已知)∴ ∠3=180°-∠1=180°-75°=105°.∵ ∠2=105°，(已知)∴ ∠2=∠3，(等量代换)∴ AB//CD.(同位角相等，两直线平行)还有其他解法吗？解：∵ ∠2=∠5，(对顶角相等) ∠2=105°，(已知) ∴ ∠5=105°. (等量代换) ∵ ∠1=75°，(已知) ∴ ∠1+∠5=180°， ∴ AB//CD.(同旁内角互补，两直线平行)除了以上两种解法，还有其他解法吗？解：∵ ∠2+∠4=180°，(邻补角互补) ∠2=105°，(已知) ∴ ∠4=180°-105°=75°. ∵ ∠1=75°，(已知) ∴ ∠1=∠4， ∴ AB//CD.(内错角相等，两直线平行)光从空气斜射入水中时，传播方向会发生偏折，这种现象叫做光的折射.同样，光从水中斜射入空气中时，也会发生折射.如图，一束光 CD 从空气射入水中，再从水中射入空气中.其中，直线 a，b 都表示空气与水的分界面，光在水中的部分为 DE.已知∠1=∠4，∠2=∠3，请你判断 CD 与 EF 是否平行？为什么？跟踪训练新知探究解：平行. 理由如下：∵∠2+∠5=180°，∠3+∠6=180°，∠2=∠3，∴∠5=∠6，又∠1=∠4，∴∠1 +∠5=∠4+∠6，即∠CDE =∠DEF，∴CD//EF.1.如图，点 E 在 BC 的延长线上，对于给出的四个条件：①∠1=∠3；②∠2+∠5=180°；③∠4=∠B；④∠D+∠BCD =180°.其中能判断 AD//BC 的是( )A.①② B.①④ C.①③ D.②④内错角AB//DCAB//DC同旁内角B随堂练习2.设 a，b，c 为同一平面内的三条直线，下列判断不正确的是( )A.若 a//b，b//c，则 a//cB.若 a⊥b，b⊥c，则 a⊥cC.若 a⊥b，b⊥c，则 a//cD.若 a//b，b⊥c，则 a⊥cB3.在如图所示的四种沿 AB 进行折叠的方法中，不一定能判断纸带两条边 a，b互相平行的是( )A.如图1，展开后测得∠1=∠2B.如图2，展开后测得∠1=∠2且∠3=∠4C.如图3，测得∠1=∠2D.在图4中，展开后测得∠1+∠2=180°内错角∠1=∠2=∠3=∠4=90°同旁内角C同位角相等，两直线平行判定两直线平行的方法内错角相等，两直线平行同旁内角互补，两直线平行同一平面内，垂直于同一直线的两直线平行平行线的定义平行公理的推论课堂小结1.如图，在下列条件中，能说明 AC//DE 的是( )A.∠A =∠CFDB.∠BED =∠EDFC.∠BED =∠AD.∠A+∠AFD =180°AB//DFAB//DFAB//DFC拓展提升AC//DE2.如图所示，一条公路修到湖边时，需要拐弯绕湖而过，第一次拐的角∠A=110°，第二次拐的角∠B=145°，则第三次拐的角∠C = 时，道路 CE 才能恰好与 AD 平行.解析：当第三次拐的角∠C = 145°时，道路 CE 才能恰好与 AD 平行.理由如下：如图，过点 B 作∠ABF = 110°.∵ ∠A =∠ABF =110°，∴ AD//BF(内错角相等，两直线平行).∵ ∠ABC =145°，∠ABF =110°，∴ ∠FBC =∠ABC -∠ABF =35°.F∵ ∠C +∠FBC =145°+35°=180°，∴ BF//CE(同旁内角互补，两直线平行)，∴ CE//AD(平行公理的推论).F3.一副直角三角尺叠放如图（1）所示，现将含 45° 的三角尺 ADE 固定不动，将含 30° 的三角尺 ABC 绕顶点 A 顺时针转动，使两块三角尺至少有一组边互相平行，如图（2），当∠BAD =15°时，BC//DE，则∠BAD(0°＜∠BAD＜180°)其他所有可能符合条件的度数为( )A.60°和135° B.45°、60°、105°和135°C.30°和45° D.以上都有可能解析：如图(1)，当∠BAD =∠DAE =45° 时, AC//DE ；如图(2)，当 ∠DAB =∠B =60° 时， BC//AD ；如图(3)，当 ∠EAB =∠B =60° 时， BC//AE ，∠BAD =∠DAE +∠EAB =45°+60°=105°；如图(4)，当 ∠E =∠EAB =90° 时， AB//DE ，∠BAD =∠DAE +∠EAB =45°+90°=135°.此类型题的专题训练见《教材帮》数学RJ七下《培优帮》培优专题二.3.一副直角三角尺叠放如图（1）所示，现将含 45° 的三角尺 ADE 固定不动，将含 30° 的三角尺 ABC 绕顶点 A 顺时针转动，使两块三角尺至少有一组边互相平行，如图（2），当∠BAD =15°时，BC//DE，则∠BAD(0°＜∠BAD＜180°)其他所有可能符合条件的度数为( )A.60°和135° B.45°、60°、105°和135°C.30°和45° D.以上都有可能B