初中数学人教版七年级下册5.2.2 平行线的判定教学ppt课件

这是一份初中数学人教版七年级下册5.2.2 平行线的判定教学ppt课件，共23页。PPT课件主要包含了由此说明了什么，同位角，解这两条直线平行，平行线的判定方法2，简单说成，还有其他解法吗，平行线的判定方法3，平行线的判定方法等内容，欢迎下载使用。

一、创设情境，引入新课
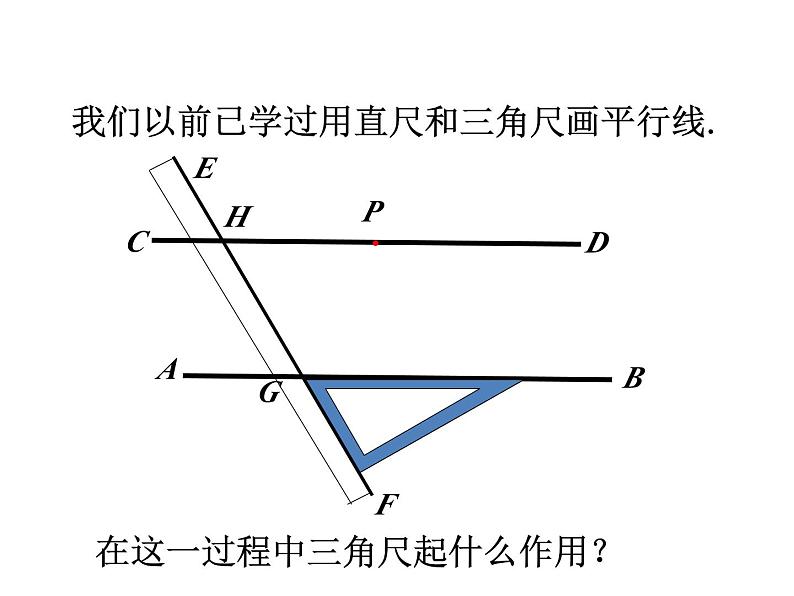
我们以前已学过用直尺和三角尺画平行线.
在这一过程中三角尺起什么作用？
二、探究直线平行的方法1
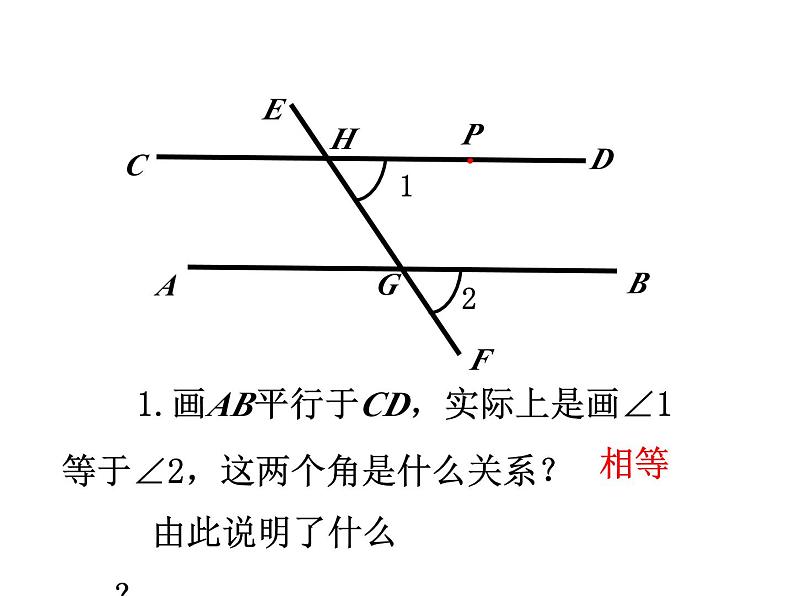
1.画AB平行于CD，实际上是画∠1等于∠2，这两个角是什么关系？
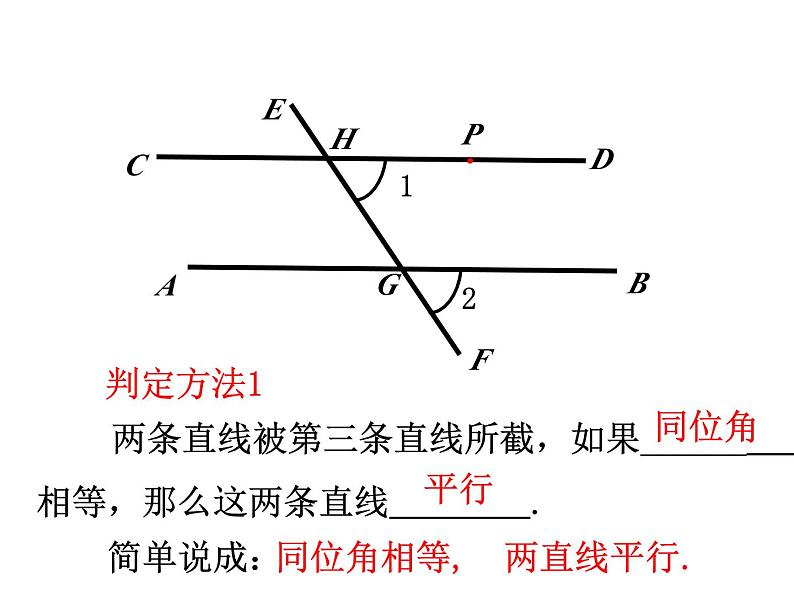
两条直线被第三条直线所截，如果______ 相等，那么这两条直线 .
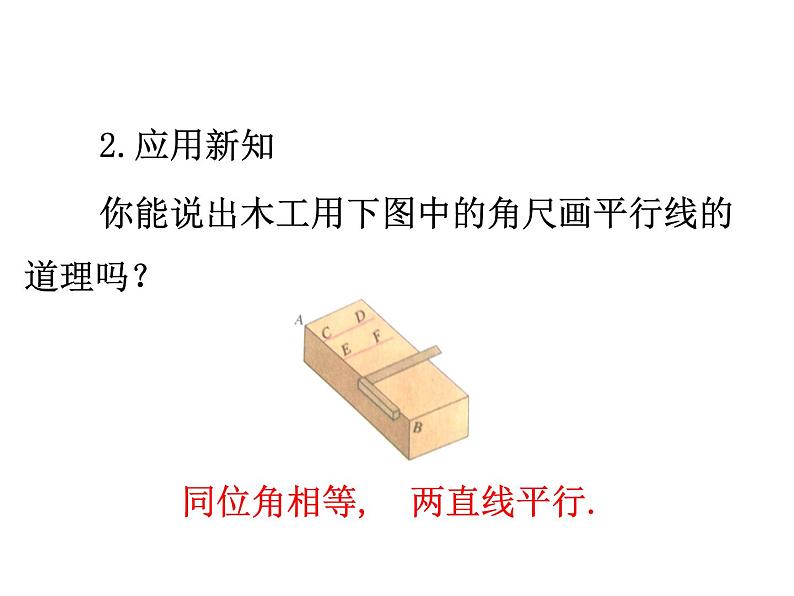
同位角相等, 两直线平行.
你能说出木工用下图中的角尺画平行线的道理吗？
例 在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行吗？为什么？
∵ b⊥a， c⊥a，∴∠1=∠2 = 90°.∴b ∥ c（同位角相等，两直线平行）.
结论：垂直于同一条直线的两条直线互相（ ）.
三、探究直线平行的其他方法
两条直线被第三条直线所截，形成的角中，有同位角、内错角和同旁内角，同位角相等, 两直线平行，那么，利用内错角、同旁内角的关系，能否判定两直线平行？
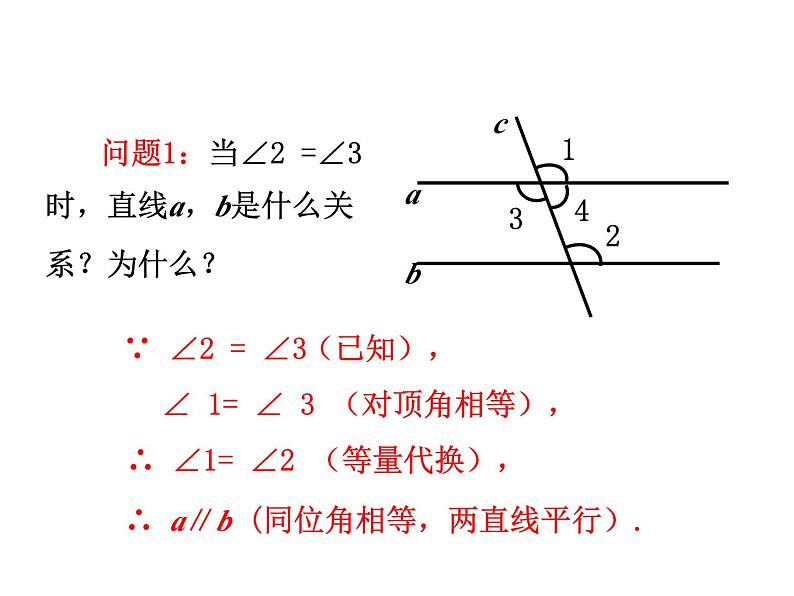
∠ 1= ∠ 3 （对顶角相等），
∴ ∠1= ∠2 （等量代换），
∴ a∥b (同位角相等，两直线平行）.
问题1：当∠2 =∠3时，直线a，b是什么关系？为什么？
两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.
内错角相等，两直线平行.
问题2：你能发现当∠2 ，∠4有怎样的关系时，直线a∥b吗？
讨论：如果∠2+∠4= 180°，能得到 a∥b吗?
∵ ∠1 + ∠4= 180°，∠2 + ∠4 = 180°，∴ ∠1 =∠2（同角的补角相等），∴ a∥b (同位角相等，两直线平行）.
同旁内角互补，两直线平行.
两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.
想一想，我们是怎样利用“同位角相等, 两直线平行”得到“内错角相等，两直线平行”和“同旁内角互补，两直线平行”的.
例 如图，b⊥a， c⊥a，直线b ，c平行吗？
你能用判定方法2解决这个问题吗？
解：∵b⊥a，c⊥a，∴∠1=90°，∠3=90° ，∴∠1=∠3， ∴b∥c（内错角相等，两直线平行）.
你能用判定方法3解决这个问题吗？
解：∵b⊥a，c⊥a，∴ ∠1=90°，∠3=90° ，∴ ∠1+∠3=180°， ∴b∥c（同旁内角互补，两直线平行）.
1.如图，BE是AB的延长线. （1）由∠CBE=∠A可以判定哪两条直线平行？根据是什么？ （2）由∠CBE=∠C可以判定哪两条直线平行？根据是什么？
解：（1）由∠CBE=∠A可以判断AD∥BC，根据是同位角相等，两条直线平行.
解：（2）由∠CBE=∠C可以判断CD∥AE，根据是内错角相等，两条直线平行．
2.在铺设铁轨时，两条直轨必须是互相平行的.如图，已经知道∠2是直角，那么再度量图中已标出的哪个角，就可以判断两条直轨是否平行？为什么？
解：①通过度量∠3的度数，若满足∠2+∠3=180°，根据同旁内角互补，两直线平行，就可以验证这个结论；②通过度量∠4的度数，若满足∠2=∠4，根据同位角相等，两直线平行，就可以验证这个结论；③通过度量∠5的度数，若满足∠2=∠5，根据内错角相等，两直线平行，就可以验证这个结论．
3.如图，这是小明同学自己制作的英语抄写纸的一部分.其中的横格线互相平行吗？你有多少种判别方法？
解：横格线互相平行．判断方法有：画一条直线与横格线相交，然后利用同位角相等判断横格线平行；或利用内错角相等判断横格线平行；或利用同旁内角互补判断横格线平行等．
补充：有一块长方形的玻璃，你能用什么方法检查它的对边是平行的？
解：可以通过测量玻璃的四个角，看相邻两个角的和是否为180°，若是，就平行．
小结：想一想，你有多少种判定直线平行的方法？
1.同位角相等, 两直线平行.
2.内错角相等，两直线平行.
3.同旁内角互补，两直线平行.
4.如果两条直线都与第三条直线平行，那么这两条直线也互相平行.
5.在同一平面内，垂直于同一条直线的两条直线互相平行.
习题5.2第2，3，4，7题.