数学8.1 基本立体图形课时练习

这是一份数学8.1 基本立体图形课时练习，共31页。试卷主要包含了1基本立体图形，棱柱的概念，棱柱的分类等内容，欢迎下载使用。

【考点梳理】
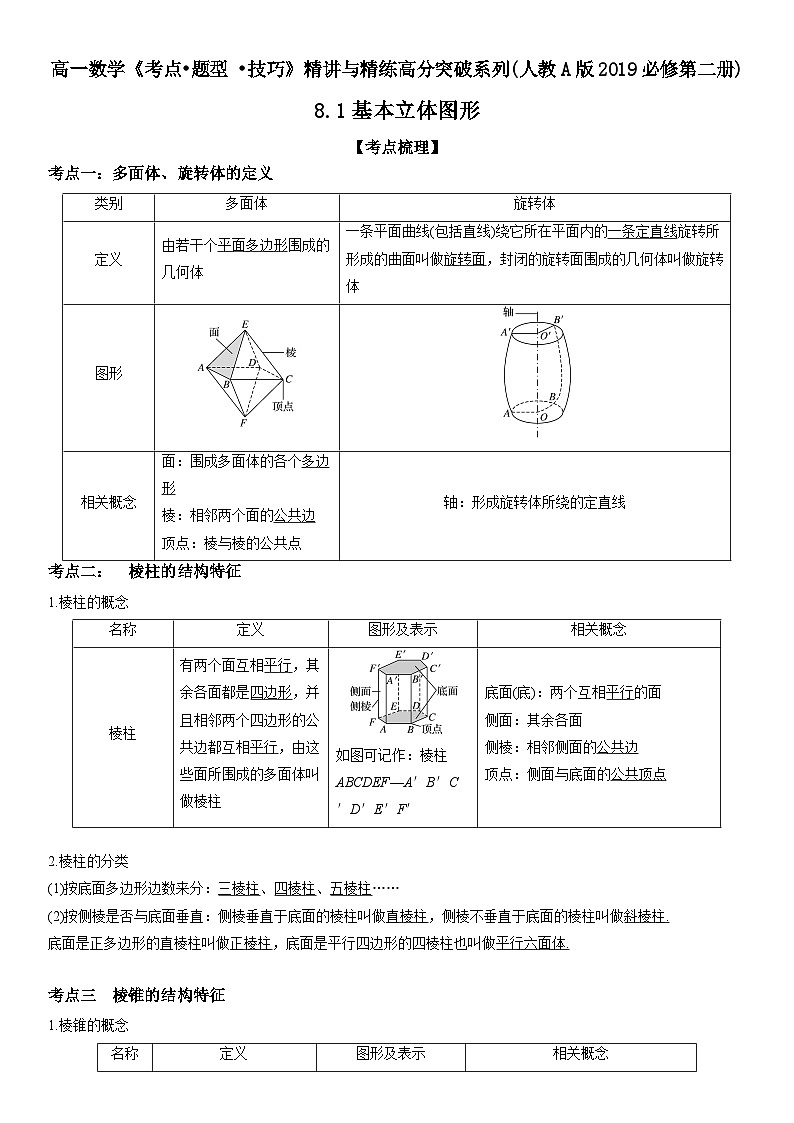
考点一：多面体、旋转体的定义
考点二： 棱柱的结构特征
1.棱柱的概念
2.棱柱的分类
(1)按底面多边形边数来分：三棱柱、四棱柱、五棱柱……
(2)按侧棱是否与底面垂直：侧棱垂直于底面的棱柱叫做直棱柱，侧棱不垂直于底面的棱柱叫做斜棱柱.
底面是正多边形的直棱柱叫做正棱柱，底面是平行四边形的四棱柱也叫做平行六面体.
考点三 棱锥的结构特征
1.棱锥的概念
2.棱锥的分类
(1)按底面多边形的边数分：三棱锥、四棱锥……
(2)底面是正多边形，并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥.
考点四：棱台的结构特征
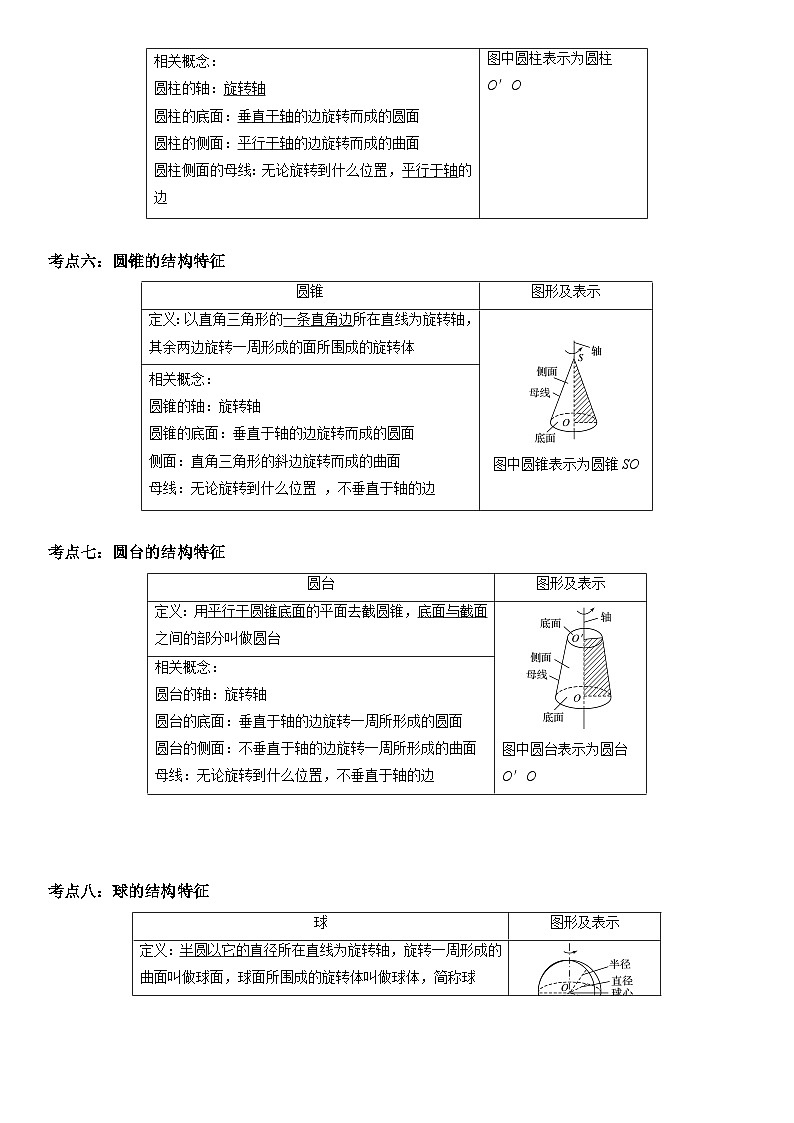
考点五：圆柱的结构特征
考点六：圆锥的结构特征
考点七：圆台的结构特征
考点八：球的结构特征
考点九：简单组合体的结构特征
1.概念：由简单几何体组合而成的，这些几何体叫做简单组合体.
2.基本形式：一种是由简单几何体拼接而成，另一种是由简单几何体截去或挖去一部分而成.
【题型归纳】
题型一：棱柱的结构特征
1．（2023·全国·高一课时练习）下列命题正确的是（ ）
A．有两个面平行，其余各面都是四边形的几何体叫棱柱
B．有两个面平行，其余各面都是平行四边形的几何体叫棱柱
C．有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱
D．棱柱的侧面都是全等的平行四边形
2．（2023·全国·高一课时练习）如图所示的几何体中棱柱的个数为（ ）
A．1B．2
C．3D．4
3．（2023·安徽安庆·高一期末）下列关于棱柱的命题中，真命题的个数是（ ）
①同一棱柱的侧棱平行且相等；
②一个棱柱至少有5个面；
③当棱柱的底面是正多边形时，该棱柱一定是正棱柱；
④当棱柱的底面是等腰梯形时，该棱柱一定是平行六面体.
A．1B．2C．3D．4
题型二：棱锥的结构特征
4．（2023·全国·高一课时练习）以下关于正棱锥的叙述不正确的是（ ）
A．正棱锥的高与底面的交点是底面的中心
B．正四棱锥的各侧面都是锐角三角形
C．正棱锥的各侧面都是等腰三角形
D．底面是正多边形且各侧面都是等腰三角形的棱锥是正棱锥
5．（2023·全国·高一课前预习）下面图形中，为棱锥的是（ ）
A．①③B．①③④C．①②④D．①②
6．（2020·河南·南阳市第四中学高一阶段练习）给出下列四个命题：
①各侧面都是全等四边形的棱柱一定是正棱柱；
②对角面是全等矩形的六面体一定是长方体；
③棱锥的侧棱长与底面多边形的边长相等，则该棱锥可能是正六棱锥；
④长方体一定是正四棱柱．
其中正确的命题个数是（ ）
A．B．C．D．
题型三：棱台的结构特征
7．（2023·山西柳林·高一期中）下列关于棱台的说法中错误的是（ ）
A．所有的侧棱所在直线交于一点
B．只有两个面互相平行
C．上下两个底面全等
D．所有的侧面不存在两个面互相平行
8．（2023·重庆市江津中学校高一开学考试）下列说法中正确的是（ ）
A．棱台的侧棱延长后必交于一点
B．两个底面平行且相似，其余各面都是梯形的多面体是棱台
C．棱台的底面是两个相似的正方形
D．用一个平面去截棱锥，棱锥底面和截面之间的部分是棱台
9．（2019·天津·高一期中）下列命题中正确的是
A．有两个面平行，其余各面都是四边形的几何体叫棱柱
B．有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱
C．用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台
D．有两个面平行，其余各面都是平行四边形的几何体叫棱柱
题型四：圆柱、圆锥、圆台的结构特征
10．（2020·全国·高一课时练习）下列命题中不正确的是（ ）
A．用平行于圆锥底面的平面截圆锥，截面与底面之间的部分是圆台
B．以直角梯形的一腰为轴，另一腰旋转形成的面是圆台的侧面
C．圆柱、圆锥、圆台的底面相似
D．圆台的母线延长后交于一点
11．（2023·全国·高一课时练习）给出下列命题：①在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线；②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线；③在圆台的上、下底面的圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的任意两条母线所在的直线是互相平行的；⑤圆台所有母线的延长线交于一点其中正确的命题是（ ）
A．①②④B．②③④C．①③⑤D．②④⑤
12．（2023·全国·高一）下列说法正确的是（ ）
A．以直角三角形的一边所在直线为轴旋转一周所得的旋转体是圆锥
B．以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台
C．圆柱、圆锥、圆台的底面都是圆面
D．一个平面截圆锥，得到一个圆锥和一个圆台
题型五：球的结构特征
13．（2023·全国·高一课时练习）下列命题正确的是( )
①过球面上任意两点只能作一个经过球心的圆；②球的任意两个经过球心的圆的交点的连线是球的直径；③用不过球心的截面截球，球心和截面圆心的连线垂直于截面；④球面上任意三点可能在一条直线上；⑤球的半径是球面上任意一点和球心的连线段.
A．①②③B．②③④
C．②③⑤D．①④⑤
14．（2020·全国·高一课时练习）下列说法中正确的个数是（ ）
①球的半径是球面上任意一点与球心的连线；
②球面上任意两点的连线是球的直径；
③用一个平面截一个球，得到的截面是一个圆；
④用一个平面截一个球，得到的截面是一个圆面；
⑤以半圆的直径所在直线为轴旋转形成的曲面叫做球；
⑥空间中到定点的距离等于定长的所有的点构成的曲面是球面.
A．0B．1C．2D．3
15．（2019·全国·高一课时练习）给出下列四个命题：①空间中，到一定点距离等于定长的点的集合是球面；②球面上不同的三点不可能在同一直线上；③过球面上不同的两点只能作一个大圆；④球的表面积是球大圆面积的4倍．其中假命题的个数是
A．0B．1C．2D．3
题型六：简单组合体问题
16．（2023·重庆一中高一阶段练习）如图所示的螺母可以看成一个组合体，对其结构特征最接近的表述是（ ）
A．一个六棱柱中挖去一个棱柱B．一个六棱柱中挖去一个棱锥
C．一个六棱柱中挖去一个圆柱D．一个六棱柱中挖去一个圆台
17．（2023·江苏徐州·高一期中）将一个等腰梯形绕它的较长的底边所在的直线旋转一周，所得的几何体包括（ ）
A．一个圆台、两个圆锥B．两个圆台、一个圆柱
C．两个圆柱、一个圆台D．一个圆柱、两个圆锥
18．（2018·湖北宜昌·高一期末（文））如图所示的几何体，关于其结构特征，下列说法不正确的是
A．该几何体是由两个同底的四棱锥组成的几何体
B．该几何体有12条棱、6个顶点
C．该几何体有8个面，并且各面均为三角形
D．该几何体有9个面，其中一个面是四边形，其余均为三角形
题型七：基本立体图形的综合性问题
19．（2022·内蒙古·呼和浩特市第十四中学高一期末）下列说法中正确的是（ ）
A．斜棱柱的侧面中可能有矩形
B．有一个面是多边形，其余各面都是三角形的几何体是棱锥
C．直角三角形绕它的一条边所在直线旋转一周形成的曲面围成的几何体是圆锥
D．棱台各侧棱的延长线不一定交于一点
20．（2023·安徽·六安一中高一阶段练习）给出下列命题∶
①棱柱的侧棱都相等，侧面都是全等的平行四边形；
②用一个平面去截棱锥，棱锥底面与截面之间的部分是棱台
③棱台的侧棱延长后交于一点，且侧面是等腰梯形，
其中正确命题的个数是（ ）
A．0B．1C．2D．3
21．（2023·河北大名·高一期中）下列结论错误的是（ ）
A．圆柱的每个轴截面都是全等矩形
B．一个棱锥至少有四个面
C．一个棱柱至少有两个面平行
D．用一个平面截圆锥，必得到一个圆锥和一个圆台
【双基达标】
一、单选题
22．（2023·河北省盐山中学高一阶段练习）棱台不具备的特点是（ ）
A．两底面相似B．侧面都是梯形
C．侧棱长都相等D．侧棱延长后都交于一点
23．（2023·陕西师大附中高一阶段练习）下列判断正确的是（ ）
A．正三棱锥一定是正四面体
B．底面是正方形的四棱锥是正四棱锥
C．底面是正方形的直四棱柱是正四棱柱
D．底面是正方形的棱台是正四棱台
24．（2023·山西·怀仁市大地学校高中部高一阶段练习）如图是一个正方体的表面展开图，则图中“有”在正方体中所在的面的对面上的是（ ）
A．者B．事C．竟D．成
25．（2020·安徽六安·高一阶段练习）下列说法正确的是（ ）
A．圆柱的母线长与圆柱的底面圆半径不可能相等
B．将一个等腰梯形绕着它较长的底边所在的直线旋转一周，所得的几何体是一个圆锥
C．侧面都是矩形的直四棱柱是长方体
D．任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥
26．（2023·河北·博野县实验中学高一期中）两平行平面截半径为13的球，若截面面积分别为和，则这两个平面间的距离是（ ）
A．7B．17
C．5或12D．7或17
27．（2023·山西灵丘·高一期中）如图，几何体是由一个圆柱挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥而得的．现用一个竖直的平面去截这个几何体，则截面图形可能是（ ）
A．B．C．D．
【高分突破】
一：单选题
28．（2023·山西高平·高一期中）有以下命题：
①以直角梯形的一腰为轴旋转所得的几何体是圆台
②棱台的两个底面一定是相似多边形
③连接圆柱的上、下底面圆周上任意两点的线段是圆柱的母线
④用平行于底面的平面截去一个小圆锥后剩余的部分是圆台
其中的正确命题的个数为（ ）
A．1B．2C．3D．4
29．（2023·山西高平·高一期中）下面四个几何体中，是棱台的是（ ）
A．B．C．D．
30．（2023·河北·邯山区新思路学本文化辅导学校高一期中）下列命题中是假命题的是（ ）
A．圆柱的任意两条母线平行B．棱台各侧棱的延长线交于一点
C．经过圆锥侧面上一点，有无数条母线D．底面是正多边形的直棱柱叫做正棱柱
31．（2023·内蒙古·集宁二中高一期末）下列结论正确的是（ ）
A．侧面都是等腰三角形的三棱锥是正三棱锥
B．用一个平面去截圆锥，底面与截面之间的部分叫圆台
C．有两个侧面是矩形的棱柱是直棱柱
D．底面是平行四边形的四棱柱是平行六面体
32．（2023·安徽宣城·高一期中）下列说法正确的是（ ）
①棱柱的侧棱都相等；
②以直角梯形的一腰为轴旋转一周所得到旋转体是圆台；
③圆锥截去一个小圆锥后剩余部分是圆台；
④通过圆台侧面上一点有无数条母线．
A．①②B．①③C．②④D．③④
33．（2023·福建福州·高一期中）下列关于空间几何体的叙述，正确的是（ ）
A．直角三角形绕它的一条边旋转得到的几何体是一个圆锥
B．棱柱的侧面都是平行四边形
C．用一个平面去截棱锥，底面和截面之间的部分组成的几何体叫棱台
D．直平行六面体是长方体
34．（2023·广西钦州·高一期末）下列说法正确的有（ ）
①棱台的各条侧棱所在的直线交于同一点；
②经过球面上不同的两点只能作一个面积最大的截面圆；
③各侧面都是正方形的四棱柱一定是正四棱柱；
④正三棱锥的各个侧面一定是全等的正三角形；
A．1个B．2个C．3个D．4个
35．（2023·重庆复旦中学高一期中）下面的几何体中棱柱有（ ）
A．个B．个C．个D．个
36．（2023·湖南·高一阶段练习）如图，在正四棱锥中，侧棱长均为4，且相邻两条侧棱的夹角为，E，F分别是线段，上的一点，则的最小值为（ ）
A．4B．4C．D．
37．（2023·安徽·合肥市第六中学高一期中）给出下列四个命题：
①底面是正多边形的棱柱是正棱柱；
②四棱柱、四棱台、五棱锥都是六面体；
③所有棱长相等的棱柱一定是直棱柱；
④直角三角形绕其一条边所在的直线旋转一周形成的几何体是圆锥．
其中正确的命题个数是（ ）
A．0B．1C．2D．3
二、填空题
38．（2023·河北·博野县实验中学高一期中）如图，底面半径为1，高为2的圆柱，在点A处有一只蚂蚁，现在这只蚂蚁要围绕圆柱由点A爬到点B，则蚂蚁爬行的最短路线的长是__________．
39．（2023·山西高平·高一期中）在棱长为6的正方体中，E是棱AB的中点，过作正方体的截面，则该截面的面积是___________．
40．（2023·重庆·铜梁一中高一阶段练习）有下列说法：
①球的半径是球面上任意一点与球心的连线；
②球的直径是球面上任意两点间的连线；
③半圆绕直径所在直线旋转后形成的几何体是球．
其中正确说法的序号是_____________．
41．（2023·吉林·长春外国语学校高一期中）下列说法正确的是_________．（填序号）．
①有一个面是多边形，其余各面都是三角形，由这些面所围成的几何体是棱锥；
②用一个平面去截棱锥，底面与截面之间部分所围成的几何体叫做棱台；
③三棱锥的任何一个面都可看作底面．
42．（2023·浙江·高一期末）已知圆锥的母线长为，圆锥的底面圆半径为，一只蚂蚁从圆锥的底面圆周上A点出发，沿圆锥侧面爬行一周回到点A，则蚂蚁爬行的最短路程为_______．
类别
多面体
旋转体
定义
由若干个平面多边形围成的几何体
一条平面曲线(包括直线)绕它所在平面内的一条定直线旋转所形成的曲面叫做旋转面，封闭的旋转面围成的几何体叫做旋转体
图形
相关概念
面：围成多面体的各个多边形
棱：相邻两个面的公共边
顶点：棱与棱的公共点
轴：形成旋转体所绕的定直线
名称
定义
图形及表示
相关概念
棱柱
有两个面互相平行，其余各面都是四边形，并且相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱
如图可记作：棱柱ABCDEF—A′B′C′D′E′F′
底面(底)：两个互相平行的面
侧面：其余各面
侧棱：相邻侧面的公共边
顶点：侧面与底面的公共顶点
名称
定义
图形及表示
相关概念
棱锥
有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥
如图可记作：棱锥S—ABCD
底面(底)：多边形面
侧面：有公共顶点的各个三角形面
侧棱：相邻侧面的公共边
顶点：各侧面的公共顶点
名称
定义
图形及表示
相关概念
分类
棱台
用一个平行于棱锥底面的平面去截棱锥，底面与截面之间那部分多面体叫做棱台
如图可记作：棱台ABCD—A′B′C′D′
上底面：平行于棱锥底面的截面
下底面：原棱锥的底面
侧面：其余各面
侧棱：相邻侧面的公共边
顶点：侧面与上(下)底面的公共顶点
由三棱锥、四棱锥、五棱锥……
截得的棱台分别叫做三棱台、四棱台、五棱台……
圆柱
图形及表示
定义：以矩形的一边所在直线为旋转轴，其余三边旋转一周形成的面所围成的旋转体叫做圆柱
图中圆柱表示为圆柱O′O
相关概念：
圆柱的轴：旋转轴
圆柱的底面：垂直于轴的边旋转而成的圆面
圆柱的侧面：平行于轴的边旋转而成的曲面
圆柱侧面的母线：无论旋转到什么位置，平行于轴的边
圆锥
图形及表示
定义：以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转一周形成的面所围成的旋转体
图中圆锥表示为圆锥SO
相关概念：
圆锥的轴：旋转轴
圆锥的底面：垂直于轴的边旋转而成的圆面
侧面：直角三角形的斜边旋转而成的曲面
母线：无论旋转到什么位置 ，不垂直于轴的边
圆台
图形及表示
定义：用平行于圆锥底面的平面去截圆锥，底面与截面之间的部分叫做圆台
图中圆台表示为圆台O′O
相关概念：
圆台的轴：旋转轴
圆台的底面：垂直于轴的边旋转一周所形成的圆面
圆台的侧面：不垂直于轴的边旋转一周所形成的曲面
母线：无论旋转到什么位置，不垂直于轴的边
球
图形及表示
定义：半圆以它的直径所在直线为旋转轴，旋转一周形成的曲面叫做球面，球面所围成的旋转体叫做球体，简称球
图中的球表示为球O
相关概念：
球心：半圆的圆心
半径：连接球心和球面上任意一点的线段
直径：连接球面上两点并经过球心的线段
【答案详解】
1．C
【解析】
【分析】
根据棱柱的特点进行辨析.
【详解】
有两个面平行,其余各面都是四边形的几何体，A错；
有两个面平行, 其余各面都是平行四边形的几何体如图所示，B错；
棱柱的侧面不一定是全等的平行四边形，D错；
由棱柱的定义，C正确.
故选：C.
2．C
【解析】
【分析】
根据棱柱的三个特征：①有两个面互相平行；②其余各面都是四边形；③侧棱互相平行，判断即可．
【详解】
解：棱柱有三个特征：①有两个面互相平行；②其余各面都是四边形；③侧棱互相平行，
本题所给几何体中②⑤不符合棱柱的三个特征，而①③④符合，所以几何体中棱柱的个数为3个．
故选：C．
3．B
【解析】
【分析】
根据棱柱的定义和特征，逐项分析即可求出结果.
【详解】
根据棱柱的特征，可知同一棱柱的侧棱平行且相等，故①正确；
三棱柱有5个面，故②正确；
根据正棱柱的定义，底面是正多边形的直棱柱是正棱柱，所以③错误；
根据平行六面体的定义可知，每个面都是平行四边形，所以④错误；
故选：B.
4．D
【解析】
【分析】
利用正棱锥的几何性质可判断各选项的正误.
【详解】
对于A选项，正棱锥的高与底面的交点是底面的中心，A对；
对于B选项，在正四棱锥中，设点在底面的射影点为点，如下图所示：
设，，则，，
，则为锐角，
易知等腰三角形中，，、均为锐角，即为锐角三角形，B对；
对于C选项，因为正棱锥的侧棱长相等，故正棱锥的各侧面都是等腰三角形，C对；
对于D选项，在三棱锥中，是边长为的等边三角形，，，
则三棱锥的底面是等边三角形，且每个侧面均为等腰三角形，但该三棱锥不是正棱锥，D错.
故选：D.
5．C
【解析】
【分析】
利用棱锥的定义对所给4个图形逐一分析判断作答.
【详解】
一般地，有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥，
显然①②④满足棱锥定义，③不满足棱锥定义，
所以①②④是棱锥，③不是棱锥.
故选：C
6．A
【解析】
【分析】
利用底面为菱形的直四棱柱可判断①的正误；利用底面为等腰梯形的直四棱柱可判断②的正误；利用正六棱锥的几何特征可判断③的正误；取长、宽、高都不相等的长方体可判断④的正误.
【详解】
对于①，底面是菱形（不是正方形）的直四棱柱满足条件，但它不是正棱柱，①错误；
对于②，底面为等腰梯形的直四棱柱的对角面全等，但它不是长方体，②错误；
对于③，如下图所示：
在正六棱锥中，六边形为正六边形，
设为正六边形的中心，则平面，
平面，则，
由正六边形的几何性质可知，为等边三角形，则，
，③错误；
对于④，在长方体中，若、、的长两两不相等，
则长方体不是正四棱柱，④错误.
故选：A.
7．C
【解析】
【分析】
根据棱台的定义可判断各选项的正误.
【详解】
由棱台的定义可知：
A.所有的侧棱所在直线交于一点，正确；
B.只有两个面互相平行，就是上、下底面平行，正确；
C.棱台的上下两个底面不全等，故C不正确；
D.所有的侧面不存在两个面互相平行，正确.
故选：C.
8．A
【解析】
【分析】
根据棱台的定义以及结构特征逐项判定，即可得出结论.
【详解】
因为棱台是棱锥被平行底面的平面所截，截面和底面间的部分，
选项D不正确；棱台各侧棱延长后必相交，选项A正确；
两个底面平行且相似，其余各面都是梯形的多面体中，
侧棱延长不一定会相交，所以不一定是棱台，选项B不正确；
棱台的底面不一定是正方形，选项C不正确.
故选：A.
9．B
【解析】
利用棱柱、棱台、棱锥的概念即可对逐个选项的正误作出判断
【详解】
在A中，如图的几何体，有两个面平行，其余各面都是四边形的几何体不是棱柱，故A错误；
在B中，由棱柱的定义得：
有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱，故B正确；
在C中，用一个平行于底面的平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台，故C错误；
在D中，如图的几何体，有两个面平行，其余各面都是平行四边形的几何体不是棱柱，故D错误．
故选B．
【点睛】
本题考查棱台、棱锥和棱柱的定义，属于简单题
10．B
【解析】
根据旋转体的结构特征进行判断.
【详解】
由圆柱、圆锥、圆台的概念及结构特征知均正确.
以直角梯形的直角腰为轴，另一腰旋转形成的面是圆台的侧面，以直角梯形的非直角腰为轴，另一腰旋转形成的面不是圆台的侧面.
故选B.
【点睛】
本题主要考查旋转体的特征性质，明确它们的特征性质是求解的关键，侧重考查直观想象的核心素养.
11．D
【解析】
圆柱母线所在的直线互相平行且与旋转轴平行，判断①错误，④正确；由圆锥母线的定义知②正确；根据圆台定义，判断③错误，⑤正确.
【详解】
由于圆柱母线所在的直线互相平行且与旋转轴平行，
而在圆柱的上、下底面的圆周上各取一点，
这两点的连线与旋转轴不一定平行，故①错误，④正确；
由圆锥母线的定义知②正确；
在圆台的上、下底面的圆周上各取一点，这两点的连线不一定是母线，
且圆台所有母线的延长线交于一点，故③错误，⑤正确.
故选：D.
【点睛】
本题考查圆柱、圆锥、圆台的定义，以及几何结构特征，属于基础题.
12．C
【解析】
【分析】
根据旋转体的定义判断.
【详解】
以直角三角形的直角边所在直线为轴旋转一周所得的旋转体是圆锥，以斜边为轴旋转一周所得的旋转体是是两个同底圆锥的组合体，A错；
以直角梯形的直角腰所在直线为轴旋转一周所得的旋转体才是圆台，B错；
圆柱、圆锥、圆台的底面都是圆面，正确；
平行于圆锥底面平面截圆锥，得到一个圆锥和一个圆台，如果截面不平行于底面，则截得的不是圆锥和圆台，D错.
故选：C.
【点睛】
本题考查旋转体的定义，掌握圆柱、圆锥、圆台的定义是解题的关键.
13．C
【解析】
【分析】
根据球体概念和性质即可求解.
【详解】
由球的概念与性质，当任意两点与球心在一条直线上时，可作无数个圆，故①错；②正确；③正确；球面上任意三点一定不共线，故④错误；根据球的半径的定义可知⑤正确.
故选：C.
14．D
【解析】
依次判断每个选项：两点的连线经过球心时才满足，②错误；截面是圆面，③错误；几何体叫做球，故⑤错误；得到答案.
【详解】
①正确；
当球面上两点的连线经过球心时，这两点的连线才是球的直径，故②错误；
③用一个平面截一个球，得到的截面是圆面，而不是一个圆，故③错误；
④正确；
曲面所围成的几何体叫做球，故⑤错误；
⑥正确；
故正确说法为①④⑥，共3个.
故选：
【点睛】
本题考查了与球相关命题的判断，意在考查学生的推断能力.
15．B
【解析】
【分析】
通过球的定义判断①的正误;利用球的性质判断②的正误;通过大圆的特征判断③的正误;通过球的表面积公式判断④的正误.
【详解】
解:对于①空间中,到一定点距离等于定长的点的集合是球面;满足球的定义, ①正确.
对于②,球面上不同的三点不可能在同一直线上;因为球的表面是曲面,过球面上不同的三点可以做一个截面圆,三点不可能在同一直线上, ②正确;
对于③过球面上不同的两点只能作一个大圆;如果两点是球的直径的两个端点,大圆有无数个, ③不正确;
对于④,球的表面积是,半径相同的圆面积是:,二者是4倍关系, ④正确.
综上错误的命题有: ③
所以B选项是正确的.
【点睛】
本题考查球的定义以及球的基本知识的应用,③是容易出错的命题.
16．C
【解析】
【分析】
根据组合体外部轮廓图的结构特征和挖掉的几何体的结构特征即可得解.
【详解】
螺母这个组合体的外部轮廓图是六棱柱，由于螺母是旋拧在螺杆上的，则挖去的部分是圆柱，选项C表述准确.
故选：C
17．D
【解析】
【分析】
根据题意，画出旋转后的几何体，观察图形，可得结果.
【详解】
从较短的底边的端点向另一底边作垂线，
两条垂线把等腰梯形分成了两个直角三角形，一个矩形，
所以一个等腰梯形绕它的较长的底边所在直线旋转一周形成的
是由一个圆柱，两个圆锥所组成的几何体，
如图所示．
故选：D.
18．D
【解析】
【分析】
根据几何体的直观图，得出该几何体的结构特征，由此判断选项A、B、C正确，选项D错误．
【详解】
根据几何体的直观图，得
该几何体是由两个同底的四棱锥组成的几何体，
且有棱MA、MB、MC、MD、AB、BC、CD、DA、NA、NB、NC和ND，共12条；
顶点是M、A、B、C、D和N共6个；
且有面MAB、面MBC、面MCD、面MDA、面NAB、面NBC、面NCD和面NDA共个，且每个面都是三角形．
所以选项A、B、C正确，选项D错误．
故选D．
【点睛】
本题考查了利用空间几何体的直观图判断几何体结构特征的应用问题，是基础题目．
19．A
【解析】
【分析】
由棱柱的概念可判断A；由棱锥的概念可判断B；由圆锥的概念可判断C；由棱台的概念可判断D
【详解】
对于A：斜棱柱的侧面中是平行四边形，有可能是矩形，故A正确；
对于B：有一个面是多边形，其余各面都是三角形，如果三角形没有公共点，该的几何体不是棱锥，故B错误；
对于C：如果绕直角三角形斜边所在直线旋转一周形成的曲面围成的几何体不是圆锥，故C错误；
对于D：棱台各侧棱的延长线一定交于一点，故D错误；
故选：A
20．A
【解析】
【分析】
根据棱柱，棱锥，棱台的性质判断各命题，由此确定正确命题的个数.
【详解】
因为棱柱的侧面不一定全等，所以①错，
用不平行与棱锥底面的平面解棱锥时，截面与底面之间的部分不是棱台，②错，
棱台的侧面不一定是等腰梯形，③错，
所以正确的命题个数为0，
故选：A.
21．D
【解析】
【分析】
对四个选项一一验证：
对于A，利用圆柱的结构特征判断；
对于B，利用棱锥的结构特征判断；
对于C，根据棱柱的概念判断；
对于D，由圆台于产生圆台的圆锥的结构特征，即可判断．
【详解】
对于A，圆柱的每个轴截面都是全等矩形，故A正确；
对于B，棱锥的侧面最少有三个，故一个棱锥最少有四个面，故B正确；
对于C，根据棱柱的概念可知，棱柱必有一组底面平行，故C正确；
对于D，用一个平行于底面的平面截圆锥才可以得到一个圆台和一个圆锥，故D错误．
故选：D
22．C
【解析】
【分析】
根据棱台的定义结构特征求解.
【详解】
根据棱台的定义知，棱台底面相似，侧面都是梯形，侧棱延长后都交于一点，
但是侧棱长不一定相等，
故选：C
23．C
【解析】
【分析】
由正四面体、正四棱锥、正四棱柱、正四棱台的定义辨析，即可判断
【详解】
正三棱锥不一定是正四面体，侧棱长与底面边长可能不相等，故A错误；
底面是正方形的四棱锥不一定是正四棱锥，顶点在底面的射影不一定是底面的中心，故B错误；
由正四棱住的概念可知，底面是正方形的直四棱柱是正四棱柱，故C正确；
底面是正方形的棱台不一定是正四棱台，原因是棱台的侧棱延长后的交点在两底面的射影不一定为正方形的中心，故D错误．
故选：C
24．A
【解析】
【分析】
直接把正方体的展开面图复原为空间图，结合正方体的结构特征，即可求解．
【详解】
根据正方体的表面展开图，换元成正方体，如图所示：
其中“者”在最里面，“有”在最外面．构成对面关系．
故选：A．
25．D
【解析】
【分析】
对于A，由圆柱的结构特征判断，对于B，由于等腰梯形分割成两个直角三角形和一个矩形，从而可判断所得的几何体，对于C，举例判断，对于D，由棱台的定义判断
【详解】
圆柱的底面半径可能与母线长相等，故A项不正确；
把等腰梯形分割成两个直角三角形和一个矩形，由旋转体的定义可知所得几何体包括一个圆柱、两个圆锥，故B项错误；
认识棱柱一般要从侧棱与底面的垂直与否和底面多边形的形状两方面去分析，当底面为梯形时，侧面都是矩形的直四棱柱不是长方体，故C项错误；
任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥，故D项正确．
故选：D
26．D
【解析】
【分析】
根据球的半径和两个截面圆的面积求出对应圆的半径，再分析出两个截面所存在的位置分别求出两个平行平面间的距离．
【详解】
解：球的半径为，设两个截面圆的半径别为，，球心到截面的距离分别为，；
球的半径为，由，得；
由，得；
如图①所示，当球的球心在两个平行平面的外侧时，
这两个平面间的距离为球心与两个截面圆的距离之差；
即；
如图②所示，当球的球心在两个平行平面的之间时，
这两个平面间的距离为球心与两个截面圆的距离之和．
即；
所以这两个平面间的距离为或．
故选：D．
27．A
【解析】
【分析】
考虑截面不经过圆柱的轴时对应的截面形状.
【详解】
当截面不过旋转轴时﹐截面图形如选项A所示．
故选：A．
28．B
【解析】
【分析】
根据圆台、棱台、圆柱的性质，逐一分析①②③④即可得答案.
【详解】
对于①：以直角梯形较长的腰为轴旋转所得的几何体不是圆台，所以①错误；
对于②：棱台的两个底面一定是相似多边形，所以②正确；
对于③：圆柱的轴截面与其侧面的交线才是圆柱的母线，所以③错误；
对于④：根据圆台的定义，可得④是正确的．
故选：B
29．B
【解析】
【分析】
根据台体、锥体概念逐一分析，即可得结果.
【详解】
A是圆台，D是棱锥，C侧棱延长没有交于一点，故不是四棱台，B是三棱台．
故选：B
30．C
【解析】
【分析】
分别根据圆柱、棱台、圆锥、正棱柱的定义即可判定.
【详解】
根据圆柱的定义，圆柱的任意一条母线都与圆柱的轴平行，故任意两条母线都平行，故A正确；
棱台是由平行于棱锥的底面平面所截得，故其侧棱延长后必交于原来棱锥的顶点，故B正确；
根据圆锥的定义，不可能有两条母线经过圆锥面上同一点，所以经过圆锥侧面上一点，有且仅有一条母线，故错误；
根据正棱柱的定义可知正确；
故选：.
31．D
【解析】
【分析】
利用正三棱锥，圆台，直棱柱、平行六面本的定义分别判断四个选项即可作答.
【详解】
对于A，三棱锥中，若，则侧面都是等腰三角形，显然底面不是正三角形，A不正确；
对于B，用一个平面去截圆锥，当且仅当底面与截面平行时，底面与截面之间的部分才是圆台，B不正确；
对于C，底面是菱形的直四棱柱，则以矩形与矩形为底面的四棱柱不是直棱柱，
而它的两个相对侧面,都是矩形，C不正确；
对于D，底面是平行四边形的四棱柱，它的六个面都是平行四边形，该四棱柱是平行六面体，D正确.
故选：D
32．B
【解析】
【分析】
结合棱柱与圆台的定义与几何特征即可判断.
【详解】
由棱柱定义可知，棱柱的侧面是平行四边形，所有侧棱都相等，①正确；以直角梯形垂直于底边的一腰为轴旋转才可以得到圆台，故②错误；用平行于底面的截面截圆锥，上部分为小圆锥，下部分为圆台，故③正确；通过圆台侧面上一点，只有一条母线，故④错误.
故选：B.
33．B
【解析】
【分析】
根据圆锥、棱柱、棱台、长方体的定义判断．
【详解】
直角三角形绕斜边所在直线旋转得到的几何体不是一个圆锥，A错；
根据棱柱定义知棱柱的侧面都是平行四边形，B正确；
用一个平行于底面的平面去截棱锥，底面和截面之间的部分组成的几何体叫棱台，C错；
底面是长方形的直平行六面体是长方体，D错．
故选：B．
34．A
【解析】
【分析】
利用空间几何体的几何特征逐一判断正误即可.
【详解】
①中，棱台的各条侧棱所在的直线交于同一点，故正确；
②中，若球面上不同的两点恰为某条直径的两个端点，则过此两点的大圆有无数个，故错误；
③中，正四棱柱的上下底面必须是正方形，故错误；
④中，正三棱锥的底面是等边三角形，侧面是全等的等腰三角形，故错误.
故选：A.
35．B
【解析】
【分析】
根据棱柱的结构特征，即可判断几何体是否为棱柱.
【详解】
由棱柱的三个特征：①有两个面相互平行；②其余各面是四边形；③侧棱相互平行.
题设各几何体中⑥⑦不完全符合棱柱的三个特征，而①②③④⑤符合.
故选：B.
36．C
【解析】
【分析】
将正四棱柱的侧面展开，利用两点间距离结合三角形知识求得结果.
【详解】
如图，将正四棱柱的侧面展开，则的最小值为．在中，，则．
故选：C.
37．B
【解析】
【分析】
利用几何体的结构特征，几何体的定义，逐项判断选项的正误即可．
【详解】
解：①底面是正多边形，侧棱与底面垂直的棱柱是正棱柱；所以①不正确；
②四棱柱、四棱台、五棱锥都是六面体；满足多面体的定义，所以②正确；
③所有棱长相等的棱柱一定是直棱柱；不满足直棱柱的定义，所以③不正确；
④直角三角形绕直角边所在的直线旋转一周形成的几何体是圆锥．所以④不正确；
故选：B．
38．
【解析】
【分析】
将圆柱侧面展开，结合两点间直线距离最短，求得最短线路的长.
【详解】
把圆柱的侧面沿剪开，然后展开成平面图形：矩形，在矩形中求最短距离即可．如图所示，连接，则即为蚂蚁爬行的最短距离．∵，且，
∴
∴蚂蚁爬行的最短路线的长为．
故答案为：
39．
【解析】
【分析】
先确定截面为等腰梯形，画出平面图形，计算即得解.
【详解】
如图，在正方体中，E是棱AB的中点，过作正方体的截面为等腰梯形．画出平面图形，过点作,垂足为.
因为，，，所以，
所以截面的面积为.
故答案为：
40．①③
【解析】
【分析】
根据球的知识确定正确的说法.
【详解】
①，球的半径是球面上任意一点与球心的连线，正确；
②，球的直径是球面上任意两点间的连线，错误，因为球的直径是最长的弦；
③，半圆绕直径所在直线旋转后形成的几何体是球，正确.
故答案为：①③
41．③
【解析】
【分析】
根据棱锥、棱台的结构特征逐一判断即可.
【详解】
①，有一个面是多边形，其余各面都是三角形，
由这些面所围成的几何体不一定是棱锥，
三角形满足有一个公共顶点，才能构成棱锥，错误；
②，用一个平行于底面的平面去截棱锥，
底面与截面之间部分所围成的几何体叫做棱台，错误；
③，三棱锥的任何一个面都是三角形，所以任何一个面都可看作底面，正确.
故答案为：③
42．
【解析】
【分析】
求得圆锥侧面展开图对应扇形的弦长，也即是最短路程.
【详解】
圆锥底面半径为，底面周长为，
所以圆锥侧面展开图对应的扇形的弧长为，
由于圆锥的母线长为，所以圆锥侧面展开图对应的扇形的圆心角为，
所以最短路程为.
故答案为：