
浙江省温州市瓯海区部分学校2023-2024学年上学期 期中联合考试 八年级数学试题
展开学校:___________姓名:___________班级:___________考号:___________
一、选择题(每题3分,共30分,每题只有一个正确答案)
1.已知关于的不等式的解在数轴上表示如图所示,则这个不等式可以是( )
A. B.
C. D.
2.已知,则下列不等式成立的是( )
A. B. C. D.
3.如图,已知,添加以下条件,不能判定的是( )
A. B. C. D.
(第7题)
(第3题) (第4题)
4.如图,是的角平分线,于点D.若,,则的度数是( )
A. B. C. D.
5.具备下列条件的中,不是直角三角形的是( )
A. B.
C.三边之比为 D.三边长分别为,,
6.三角形两边长为2,5,则第三条边的长可能为( )
A.2 B.3 C.5 D.7
7.如图,已知是中,的平分线的交点,交于点,交
于点.若,则的周长为( )
A. B. C. D.
8.下列选项中,可以用来说明命题“若a2>b2则a>b”是假命题的反例为( )
A.a=3,b=﹣2B.a=﹣3,b=2C.a=2,b=1D.a=﹣2,b=3
如图,已知点在的边上,,点,在边上.若,,则的长为( )
A.6 B.8 C. D.9
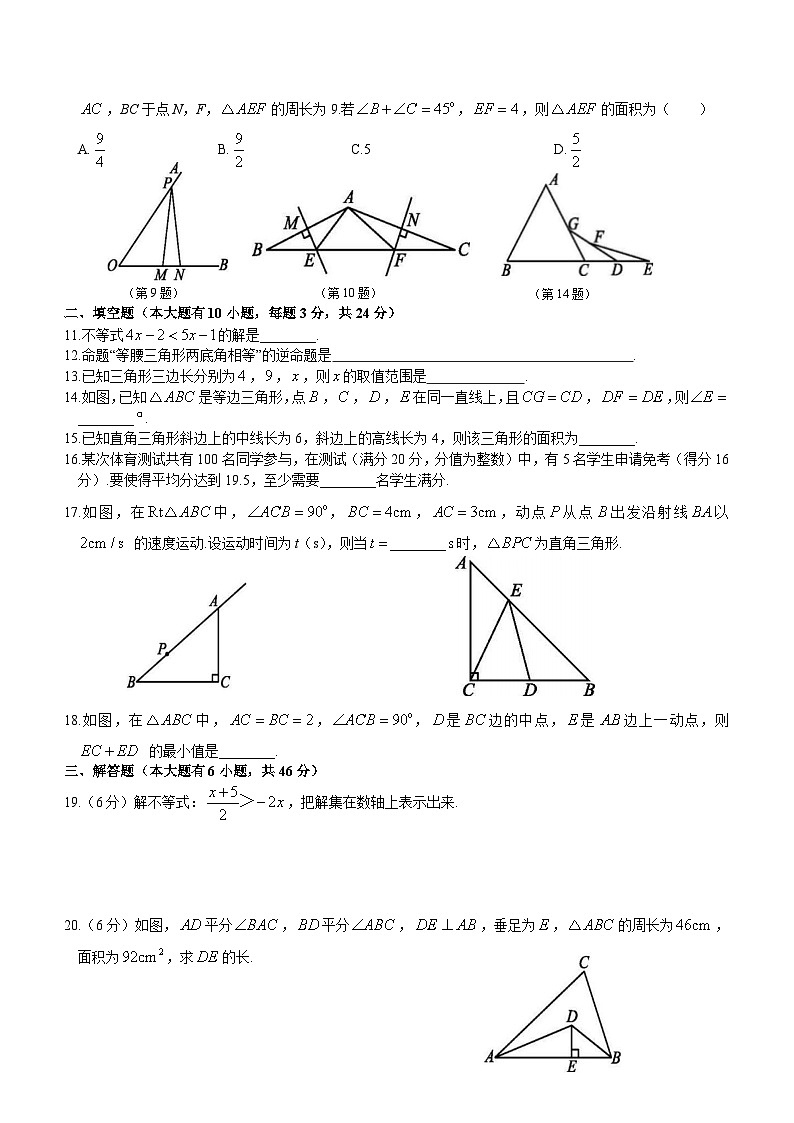
10.如图,在中,边的垂直平分线分别交,于点,,边的垂直平分线分别交,BC于点N,F,的周长为9.若,,则的面积为( )
A. B. C.5 D.
(第14题)
(第9题) (第10题)
二、填空题(本大题有10小题,每题3分,共24分)
11.不等式的解是________.
12.命题“等腰三角形两底角相等”的逆命题是 .
13.已知三角形三边长分别为,,,则的取值范围是 .
14.如图,已知是等边三角形,点,,,在同一直线上,且,,则________.
15.已知直角三角形斜边上的中线长为6,斜边上的高线长为4,则该三角形的面积为________.
16.某次体育测试共有100名同学参与,在测试(满分20分,分值为整数)中,有5名学生申请免考(得分16分).要使得平均分达到19.5,至少需要________名学生满分.
17.如图,在中,,,,动点从点出发沿射线以 的速度运动.设运动时间为t(s),则当________时,为直角三角形.
18.如图,在中,,,是边的中点,是边上一动点,则 的最小值是________.
三、解答题(本大题有6小题,共46分)
19.(6分)解不等式:,把解集在数轴上表示出来.
20.(6分)如图,平分,平分,,垂足为,的周长为,面积为,求的长.
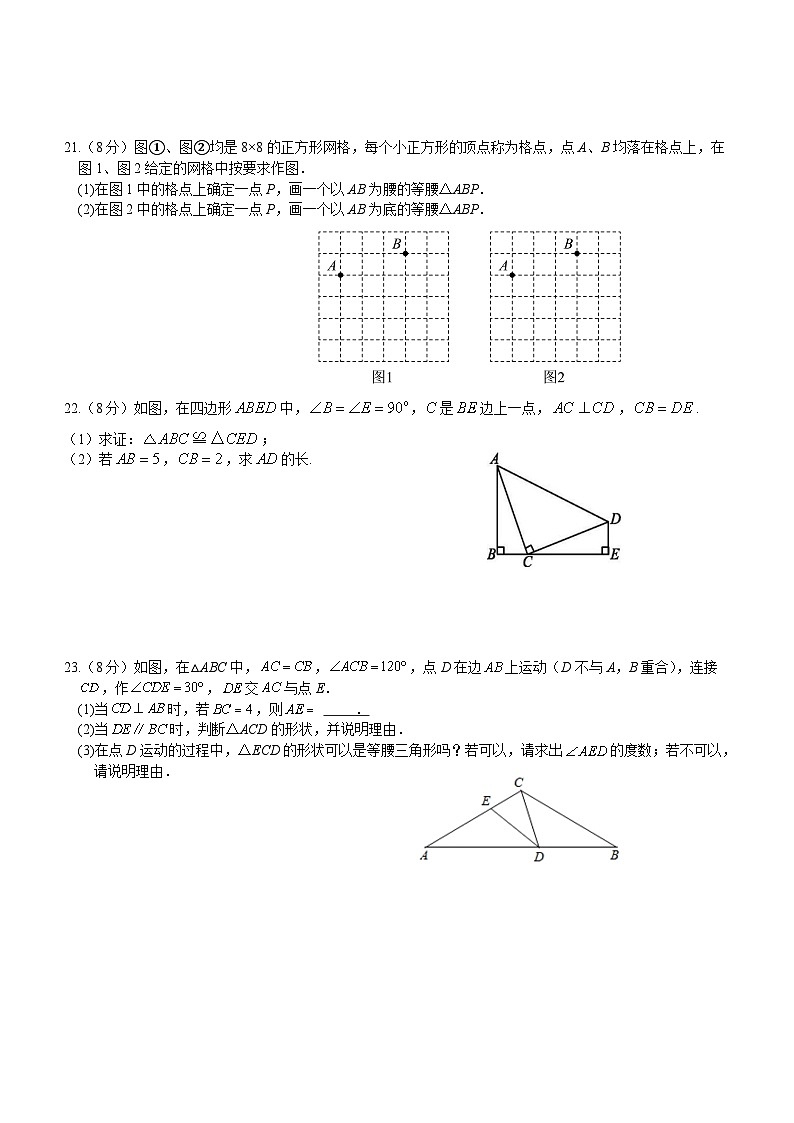
21.(8分)图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,点A、B均落在格点上,在图1、图2给定的网格中按要求作图.
(1)在图1中的格点上确定一点P,画一个以AB为腰的等腰△ABP.
(2)在图2中的格点上确定一点P,画一个以AB为底的等腰△ABP.
22.(8分)如图,在四边形中,,是边上一点,,.
(1)求证:;
(2)若,,求的长.
23.(8分)如图,在△ABC中,,,点D在边上运动(D不与A,B重合),连接,作,交与点E.
(1)当时,若,则 .
(2)当时,判断△ACD的形状,并说明理由.
(3)在点D运动的过程中,△ECD的形状可以是等腰三角形吗?若可以,请求出的度数;若不可以,请说明理由.
24.(10分)等腰中,,.
(1)如图1,,是等腰斜边上两动点,且,将△ABE绕点逆时针旋转后,得到△AFC,连接.
①求证:△AED≌AFD.
②当,时,求的长;
(2)如图2,点是等腰斜边所在直线上的一动点,连接,以点为直角顶点作等腰Rt△ADE,当,时,则的长 __________.(直接给出答案).
八年级数学试卷
一、选择题(本大题有10小题,每题3分,共30分)
1-5 ACDAB 6-10 AABCA
二、填空题(本大题有10小题,每题3分,共30分)
11. 12.有两个角相等的三角形是等腰三角形
13. 14. 15.24 16.65 17.或 18.
三、解答题(本大题有6小题,共40分)
19.(1) (2)
20.解:如图,连结CD.
平分,平分,
点D到,,的距离相等,即为的长.
的周长为,面积为,
,
即,解得.
21.(1)解:如图1,点P即为所求(答案不唯一).
(2)如图2,点P即为所求(答案不唯一).
22.解:(1)证明:如图.
,
.
,
,
.
在和中,
.
(2),
.
,,
在中,由勾股定理,得,
,
在中,由勾股定理,得.
23.(1)如图,
∵在中,,,
∴,
∵,
∴,
∵,
∴,
在中,,
∴,
同理可得:,
∵,
∴;
(2)∵中,,
∴,
∵,
∴,
又∵,
∴,
∴,
∴是直角三角形;
(3)可以是等腰三角形.理由如下:
①当时,,
∴,
∵,
∴,
②当时,,
∵,
∴,
∴,
③当时,,
即,
∵,
∴此时,点D与点B重合,不合题意.
综上,可以是等腰三角形,此时的度数为或.
24.(1)证明:如图1中,
,
,,
,,
,
,
在和中,
,
.
解:如图1中,设,则.
,,
,
,
,
,
,
在中,∵,,
∴,解得,
∴.
(2)解:当点在线段上时,如图2中所示,连接:
当点在线段的延长线上,如图3中所示,连接:
同法可证是直角三角形
浙江省温州市瓯海区部分学校2023-2024学年八年级上学期期中数学试题(原卷+解析): 这是一份浙江省温州市瓯海区部分学校2023-2024学年八年级上学期期中数学试题(原卷+解析),文件包含精品解析浙江省温州市瓯海区部分学校2023-2024学年八年级上学期期中数学试题原卷版docx、精品解析浙江省温州市瓯海区部分学校2023-2024学年八年级上学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
浙江省温州市瓯海区部分学校2023-2024学年七年级上学期期中数学试题(原卷+解析): 这是一份浙江省温州市瓯海区部分学校2023-2024学年七年级上学期期中数学试题(原卷+解析),文件包含精品解析浙江省温州市瓯海区部分学校2023-2024学年七年级上学期期中数学试题原卷版docx、精品解析浙江省温州市瓯海区部分学校2023-2024学年七年级上学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。
浙江省温州市瓯海区瓯海区实验中学2023-2024学年八年级上学期期中数学试题: 这是一份浙江省温州市瓯海区瓯海区实验中学2023-2024学年八年级上学期期中数学试题,共24页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












