初中数学人教版八年级上册12.1 全等三角形课后作业题

这是一份初中数学人教版八年级上册12.1 全等三角形课后作业题，共4页。试卷主要包含了1全等三角形等内容，欢迎下载使用。
第12章 全等三角形第1课时  12.1全等三角形
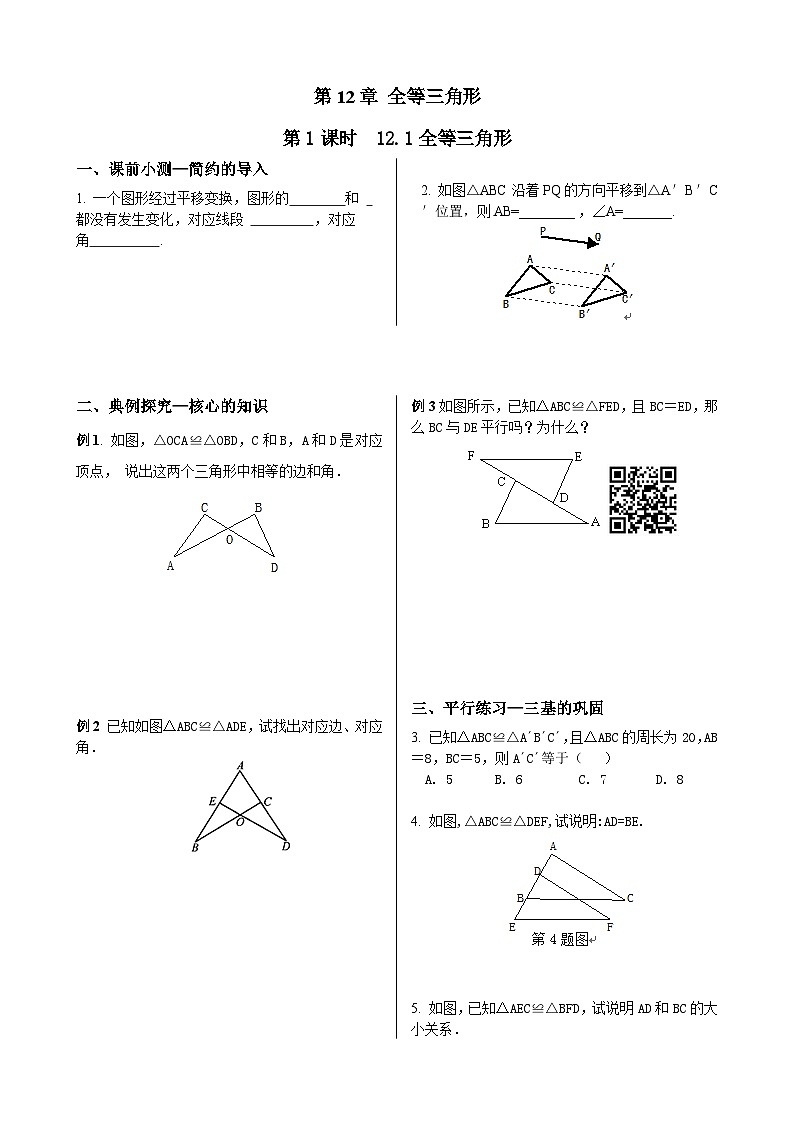
一、课前小测—简约的导入1. 一个图形经过平移变换，图形的        和          都没有发生变化，对应线段          ，对应角          .    2. 如图△ABC沿着PQ的方向平移到△A′B′C′位置，则AB=________，∠A=_______.
  
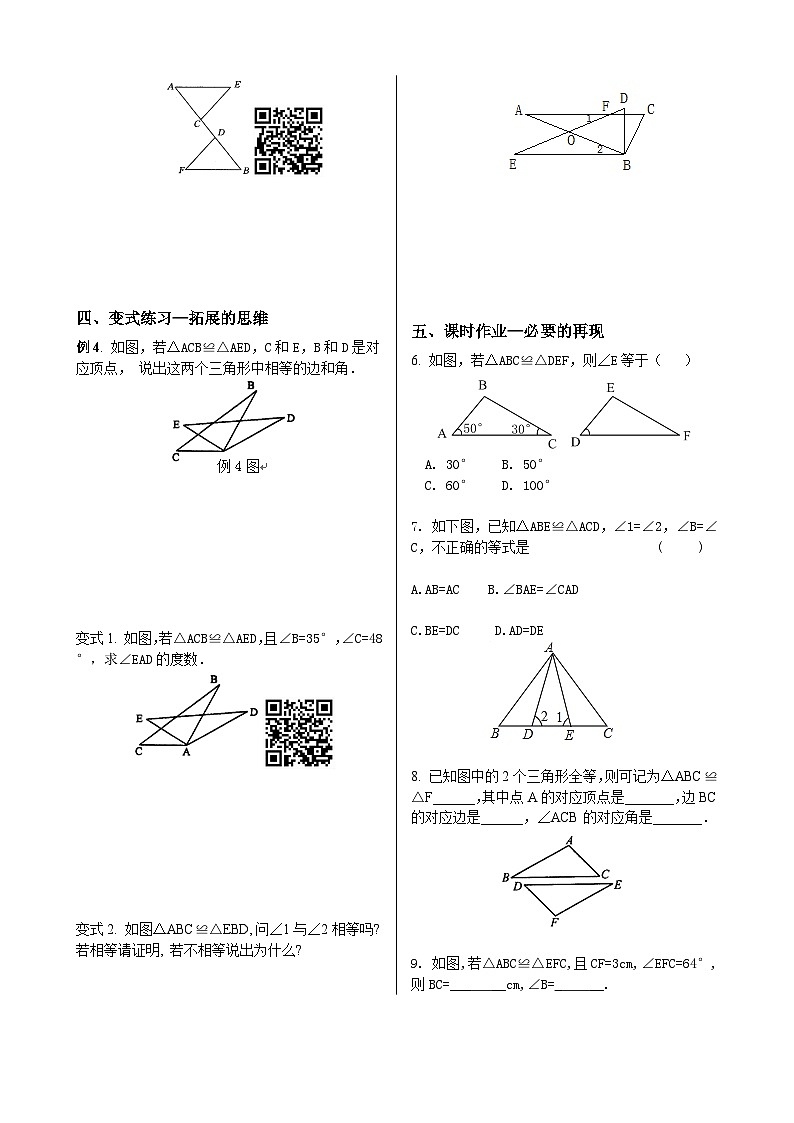
二、典例探究—核心的知识例1. 如图，△OCA≌△OBD，C和B，A和D是对应顶点，说出这两个三角形中相等的边和角．     例2 已知如图△ABC≌△ADE，试找出对应边、对应角．        例3如图所示，已知△ABC≌△FED，且BC＝ED，那么BC与DE平行吗？为什么？    三、平行练习—三基的巩固3. 已知△ABC≌△A´B´C´，且△ABC的周长为20，AB＝8，BC＝5，则A´C´等于（   ）A. 5     B. 6        C. 7    D. 8 4. 如图,△ABC≌△DEF,试说明:AD=BE.  5. 如图，已知△AEC≌△BFD，试说明AD和BC的大小关系．    四、变式练习—拓展的思维例4. 如图，若△ACB≌△AED，C和E，B和D是对应顶点，说出这两个三角形中相等的边和角．       变式1. 如图，若△ACB≌△AED，且∠B=35°，∠C=48°，求∠EAD的度数．       变式2. 如图△ABC≌△EBD,问∠1与∠2相等吗?若相等请证明, 若不相等说出为什么?     五、课时作业—必要的再现6. 如图，若△ABC≌△DEF，则∠E等于（   ）A. 30°  B. 50°  C. 60°    D. 100° 7. 如下图，已知△ABE≌△ACD，∠1=∠2，∠B=∠C，不正确的等式是                  (     ) A.AB=AC    B.∠BAE=∠CAD C.BE=DC     D.AD=DE 8. 已知图中的2个三角形全等，则可记为△ABC≌△F______，其中点A的对应顶点是_______，边BC的对应边是______，∠ACB的对应角是_______． 9. 如图,若△ABC≌△EFC,且CF=3cm,∠EFC=64°,则BC=___   __cm,∠B=_    __.   答案:1. 形状，大小，相等，相等.2．A′B′, ∠A′.例1.解：因为C和B、A和D是对应顶点，所以C和B重合，A和D重合．∠C=∠B；∠A=∠D；∠AOC=∠DOB．AC=DB；OA=OD；OC=OB．例2.解:对应边为AB与AD、AC与AE、BC与DE．对应角为∠A与∠A、∠B与∠D、∠ACB与∠AED．例3.解：∵△ABC≌△FED，∴∠BCD=∠EDC.∴BC∥DE.3.C4.解：∵△ABC≌△DEF,∴AB=DE.∴AB-BD=DE-BD.∴AD=BE.5.解:AD=BC．    理由：∵△AEC≌△BFD，    ∴AC=BD（全等三角形对应边相等），    ∴AC+CD=BD+CD，即AD=BC．例4 解:∠C=∠E；∠CAB=∠EAD；∠B=∠D．AD=AB；AE=AC；BC=DE．变式1.解: 在△ABC中，∠B=35°，∠C=48°，       ∴∠CAB=97°,       ∵△ACB≌△AED，       ∴∠EAD=∠CAB=97°变式2. 解：∠1=∠2.∵△ABC≌△EBD,∴∠A=∠E.在△AOF和△EOB中，∵∠A=∠E，∠AOF=∠EOB，∴∠1=∠2.6．D7．D8.ED, F, DE, ∠EDF9. 3, 64°