初中数学第十二章 全等三角形12.1 全等三角形优秀教案设计
展开【教材分析】
【教学流程】
教
学
目
标
知识
技能
1.复习全等三角形的概念、性质和判定方法,能够利用三角形全等进行证明;
2.复习角平分线的性质、判定方法,并利用角平分线的性质、判定进行证明问题
3.回顾复习全章知识,梳理知识点,形成全章知识框架;
过程
方法
通过有理有据的推理证明、精炼准确地表达推理过程,注重分析思路,学会思考问题,注重书写格式,学会清楚地表达思考的过程.
情感
态度
通过师生共同的探究活动,进一步培养学生合作交流的意识和大胆猜想、乐于探究的良好品质以及发展基本的创新意识和培养逻辑思维能力和.
重点
掌握全等三角形的性质与判定方法.
难点
对全等三角形性质及判定方法的运用.
环节
导 学 问 题
师 生 活 动
二次备课
知
识
回
顾
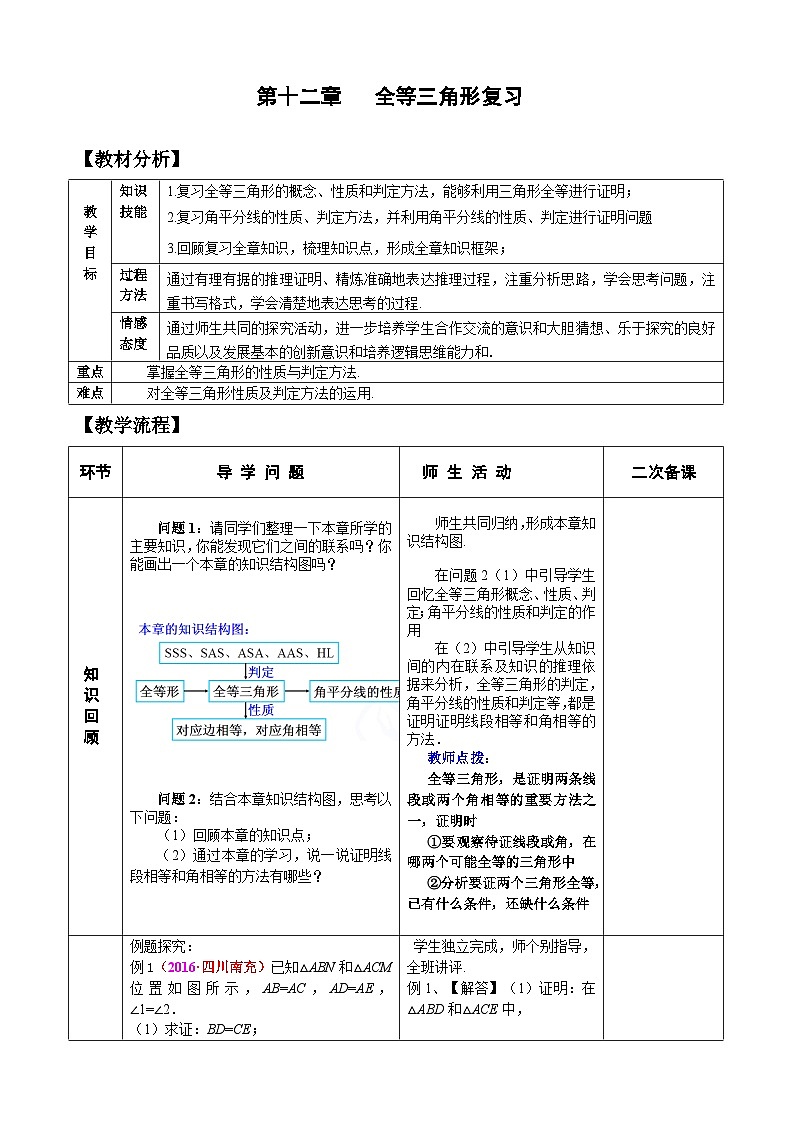
问题1:请同学们整理一下本章所学的主要知识,你能发现它们之间的联系吗?你能画出一个本章的知识结构图吗?
问题2:结合本章知识结构图,思考以下问题:
回顾本章的知识点;
(2)通过本章的学习,说一说证明线段相等和角相等的方法有哪些?
师生共同归纳,形成本章知识结构图.
在问题2(1)中引导学生回忆全等三角形概念、性质、判定;角平分线的性质和判定的作用
在(2)中引导学生从知识间的内在联系及知识的推理依据来分析,全等三角形的判定,角平分线的性质和判定等,都是证明证明线段相等和角相等的方法.
教师点拨:
全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时
①要观察待证线段或角,在哪两个可能全等的三角形中
②分析要证两个三角形全等,已有什么条件,还缺什么条件
合
作
交
流
例题探究:
例1(2016·四川南充)已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)求证:BD=CE;
(2)求证:∠M=∠N.
【分析】(1)由SAS证明△ABD≌△ACE,得出对应边相等即可
(2)证出∠BAN=∠CAM,由全等三角形的性质得出∠B=∠C,由AAS证明△ACM≌△ABN,得出对应角相等即可.
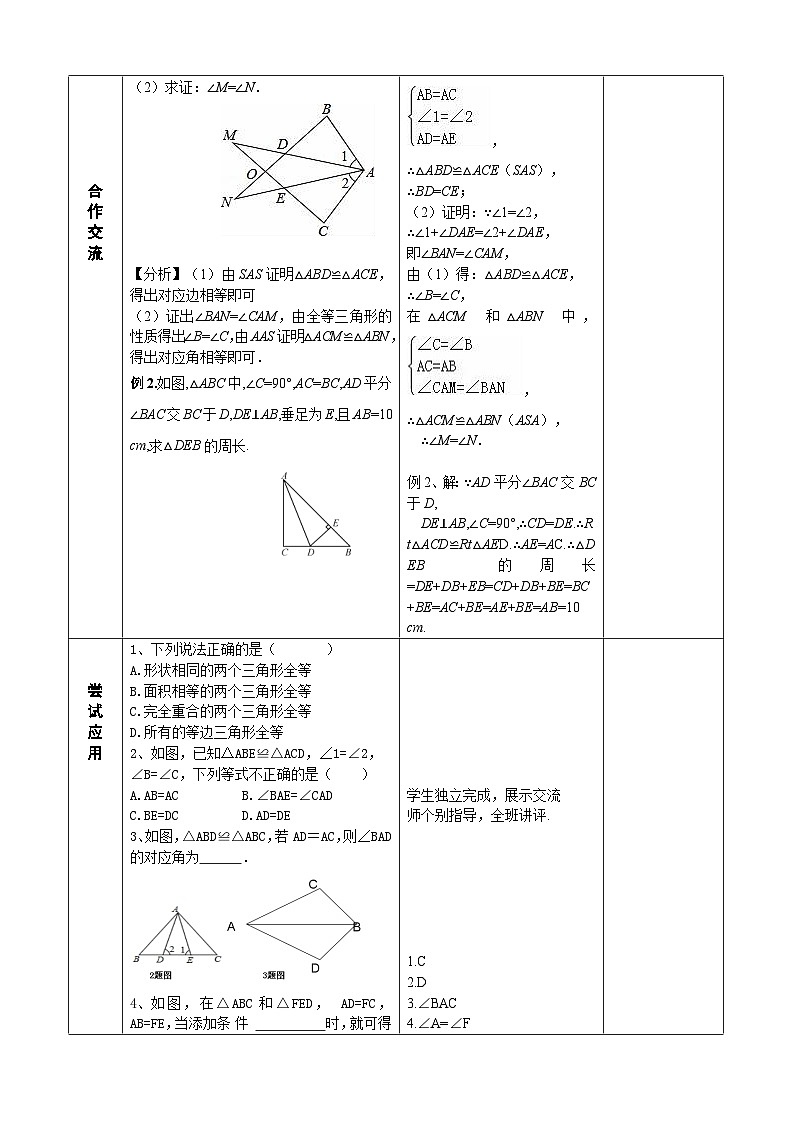
例2.如图,△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB,垂足为E,且AB=10 cm,求△DEB的周长.
学生独立完成,师个别指导,全班讲评.
例1、【解答】(1)证明:在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)证明:∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,
即∠BAN=∠CAM,
由(1)得:△ABD≌△ACE,
∴∠B=∠C,
在△ACM和△ABN中,,
∴△ACM≌△ABN(ASA),
∴∠M=∠N.
例2、解:∵AD平分∠BAC交BC于D,
DE⊥AB,∠C=90°,∴CD=DE.∴Rt△ACD≌Rt△AED.∴AE=AC.∴△DEB的周长=DE+DB+EB=CD+DB+BE=BC+BE=AC+BE=AE+BE=AB=10 cm.
尝
试
应
用
1、下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
如图,已知△ABE≌△ACD,∠1=∠2,
∠B=∠C,下列等式不正确的是( )
A.AB=AC B.∠BAE=∠CAD
C.BE=DC D.AD=DE
3、如图,△ABD≌△ABC,若AD=AC,则∠BAD的对应角为 .
如图,在△ABC和△FED, AD=FC,AB=FE,当添加条 件 时,就可得到 △ABC≌△FED.(只需填写一个你认为正确的条件)
5、如图,在△ABC中,∠C=90°, AD平分∠CAB,BC=8 cm,BD=5 cm,那么点D到直线AB的距离是 cm.
6、如图,已知△ABC的周长是21,OB, OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是 .
7、已知:如图,BE⊥CD,BE=DE,
BC=DA,求证:(1) △BEC≌△DAE;
(2)DF⊥BC.
学生独立完成,展示交流
师个别指导,全班讲评.
C
D
∠BAC
4.∠A=∠F
3
7.证明:
∵BE⊥CD
∴∠BEC=∠DEA=90°
又BE=DE,BC=DA
∴△BEC≌△DAE
由(1)得
△BEC≌△DAE,
∴∠C=∠DAE,
又∵∠DAE+∠D=90°
∴∠C+∠D=90°,
∴∠DFA=90°,∴DF⊥BC
成
果
展
示
判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
师生共同总结、反思,教师重点强调
补
偿
提
高
8已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
求证:AM平分∠DAB(提示:过点M作AD的垂线段)
学生独立完成,师个别指导,全班讲评.
8.证明:过点M作MF⊥AD,垂足为F,则∠DFM=90°
∵DM平分∠ADC
∴∠FDM=∠CDM
又∵∠DFM=∠C=90°,
DM=DM
∴△DFM≌△DCM
∴FM=CM
又∵点M是BC的中点. ∴BM=CM
∴在RT△ABM和RT△AFM中,AM=AM,FM=BM
∴RT△ABM≌RT△AFM
∴∠FAM=∠BAM
∴AM平分∠DAB
人教版八年级上册12.1 全等三角形优秀教学设计: 这是一份人教版八年级上册12.1 全等三角形优秀教学设计,共9页。教案主要包含了内容和内容解析,目标和目标分析,教学问题诊断分析,教学过程设计等内容,欢迎下载使用。
初中数学12.1 全等三角形精品教学设计: 这是一份初中数学12.1 全等三角形精品教学设计,共6页。教案主要包含了教学目标,教学重点,教学难点,教学过程,板书设计等内容,欢迎下载使用。
初中数学12.1 全等三角形教学设计及反思: 这是一份初中数学12.1 全等三角形教学设计及反思,共9页。教案主要包含了情境导入,考点题型,巩固练习,综合训练等内容,欢迎下载使用。













