人教A版 (2019)4.1 指数说课ppt课件

这是一份人教A版 (2019)4.1 指数说课ppt课件，共39页。PPT课件主要包含了目录索引等内容，欢迎下载使用。

基础落实·必备知识全过关
重难探究·能力素养全提升
学以致用·随堂检测全达标
知识点一:指数函数的概念1.一般地,函数y=ax(a>0,且a≠1)叫做指数函数.其中指数x是自变量,定义域为R.2.指数函数的特征: 判断函数是否为指数函数的标准(1)底数a>0,且a≠1;(2)指数幂的系数是1.名师点睛根据指数函数的定义,只有形如y=ax(a>0,且a≠1)的函数才是指数函数.
微思考指数函数为什么要规定a>0,且a≠1?
提示 如果a<0,那么ax对某些x值没有意义,如 无意义;如果a=0,那么当x>0时,ax=0,当x≤0时,ax无意义;如果a=1,y=1x=1是个常数函数,没有研究的必要.所以规定a>0,且a≠1,此时x可以是任意实数.
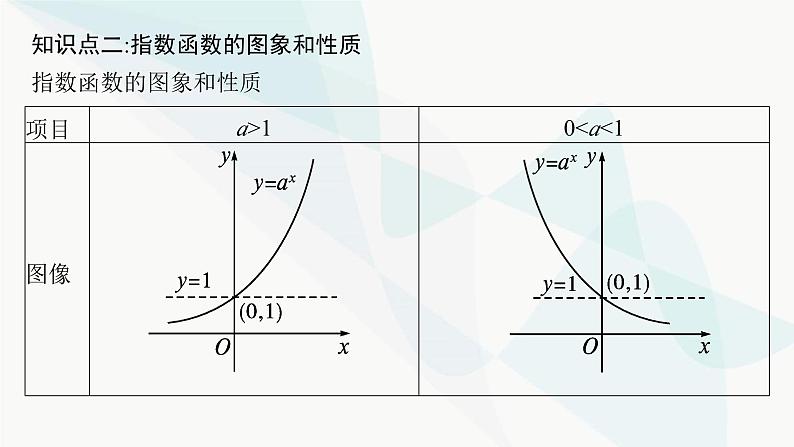
知识点二:指数函数的图象和性质指数函数的图象和性质
微思考指数函数y=ax(a>0,且a≠1)的图象“升”“降”主要取决于什么?具体变化特征是什么?
提示 指数函数y=ax(a>0,且a≠1)的图象“升”“降”主要取决于字母a.当a>1时,图象具有上升趋势,当x>0时底数a的值越大,函数图象“越陡”,函数值增长得越快;当0问题1增长率是刻画事物变化规律很重要的量,如何研究此类指数增长或衰减的函数模型?问题2通过分数指数幂的性质,思考指数函数的底数为什么要大于0?问题3类比幂函数的定义,如何给指数函数下定义?
探究点一 指数函数的概念
问题4如何根据指数函数的定义求指数函数的解析式?【例1】 (1)如果指数函数y=f(x)的图象经过点(-2, ),那么f(4)f(2)等于　　　　　. 
(2)已知函数y=(a2-3a+3)ax是指数函数,求a的值.
规律方法　指数函数是一个形式定义,其特征如下:
问题5在同一个坐标轴画出几个不同的指数函数,根据这几个指数函数的图象思考:指数函数的增减速度与底数有什么关系?问题6观察几个指数函数的图象,认真理解何为“定点”.思考:我们能否说函数y=2x的定点是(0,1)呢?
探究点二 指数函数的图象
问题7你能用描点法画出指数函数的图象吗?怎么取点合适呢?【例2】 在同一直角坐标系中画出函数y=3x和y=( )x的图象,并说明它们的关系.
两个函数的图象关于y轴对称.
探究点三 指数函数的图象及应用
问题8如何利用指数函数图象的定点求指数型函数图象的定点?【例3】 已知函数f(x)=ax+1+3(a>0,且a≠1)的图象一定过点P,则点P的坐标是　　　　　. 
解析 ∵当x+1=0,即x=-1时,f(-1)=a0+3=4恒成立,故函数f(x)=ax+1+3的图象恒过点(-1,4).
延伸探究若本例中的函数改为f(x)=5a3x-2+3呢?
规律方法　指数型函数图象过定点问题的解法因为函数y=ax的图象恒过定点(0,1),所以对于函数f(x)=kag(x)+b(k,a,b均为常数,且k≠0,a>0,且a≠1).若g(m)=0,则f(x)的图象过定点(m,k+b),即令指数等于0,解出相应的x,y,则点(x,y)为所求点.
问题9如何利用指数函数图象的性质求参数?【例4】 [2023山东枣庄高一月考]函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是(　　)A.a>1,b<0B.a>1,b>0C.00D.0解析 由于f(x)的图象单调递减,所以00,b<0,故选D.
规律方法　指数函数图象问题的处理技巧(1)抓住图象上的特殊点,如指数函数的图象过定点、特殊点的函数的值的符号等;(2)利用图象变换,如函数图象的平移变换(左右平移、上下平移);(3)利用函数的奇偶性与单调性,奇偶性确定函数的对称情况,单调性决定函数图象的走势.
问题10能由指数函数的图象画出指数型函数的图象吗?【例5】 画出函数y=( )|x|的图象,这个图象有什么特征?你能根据图象指出它的值域和单调区间吗?
∵y=( )x(x>0)和y=2x(x<0)的图象关于y轴对称,∴原函数的图象关于y轴对称.由图象可知值域是(0,1],单调递增区间是(-∞,0],单调递减区间是(0,+∞).
规律方法　指数函数y=ax与y=( )x(a>0,且a≠1)的图象关于y轴对称.处理函数图象问题的常用方法:一是抓住图象上的特殊点;二是利用图象的变换;三是利用函数的奇偶性与单调性.
探究点四 利用指数函数的单调性比较幂值大小
问题11如何利用指数函数的单调性比较两个数的大小?【例6】 比较下列各题中两个值的大小:(1)2.53,2.55.7;
解 (单调性法)由于2.53与2.55.7的底数是2.5,故构造函数y=2.5x,而函数y=2.5x在R上是增函数.又3<5.7,∴2.53<
(2)1.5-7,( )4;
(3)2.3-0.28,0.67-3.1;
解 (中间量法)由指数函数的性质,知2.3-0.28<2.30=1,0.67-3.1>0.670=1,则2.3-0.28<0.67-3.1.
(4)(a-1)1.3,(a-1)2.4(a>1,且a≠2).
解∵a>1,且a≠2,∴a-1>0,且a-1≠1.若a-1>1,即a>2,则y=(a-1)x是增函数,∴(a-1)1.3<(a-1)2.4.若0(a-1)2.4.故当a>2时,(a-1)1.3<(a-1)2.4;当1(a-1)2.4.
规律方法　比较幂的大小的常用方法
1.(例1对点题)下列函数中是指数函数的是　　　　　. 
解析 因为形如y=ax(a>0,且a≠1)的函数为指数函数,所以函数y=( )x符合指数函数的定义,是指数函数;y=4x符合指数函数的定义,是指数函数;其他函数不符合指数函数的定义,不是指数函数.
(1)在给出的坐标系中画出函数f(x)的图象.(2)根据图象写出函数的单调区间和值域.
解 (1)利用指数函数和一次函数的图象特征即可画出分段函数
(2)由函数的图象可知,函数f(x)的单调递增区间为(-∞,0],单调递减区间为[0,+∞),函数f(x)的值域为(-∞,1].
3.(例3对点题)若a>3,则函数f(x)=4(a-2)2x+6-1的图象恒过定点的坐标是　　　　　. 
解析 ∵a>3,∴a-2>1.令2x+6=0,得x=-3,则f(-3)=4(a-2)0-1=3.故函数f(x)的图象恒过定点的坐标是(-3,3).
4.(例4对点题)函数y=ax- (a>0,a≠1)的图象可能是(　　)
A.①③B.②①C.④D.①
5.(例5对点题)函数y=2-|x|的图象为下面选项中的(　　)
解析 由函数的解析式,得该函数的定义域为R,当x=0时,y=20=1,即函数图象过点(0,1),可排除选项A;当x>0时,y=2-|x|=2-x=( )x,函数y=( )x在(0,+∞)上是单调递减的,可排除选项B,D.故选C.