人教A版 (2019)必修 第一册4.1 指数示范课课件ppt

这是一份人教A版 (2019)必修 第一册4.1 指数示范课课件ppt，共37页。PPT课件主要包含了目录索引等内容，欢迎下载使用。
基础落实·必备知识全过关
重难探究·能力素养全提升
学以致用·随堂检测全达标
学习单元1　指数与指数函数
第三章“函数的概念与性质”的学习,我们初步掌握了研究函数的一般途径:概念—图象—性质—应用.并在学习的过程中,逐步体会用函数的思想解决问题的基本思路.指数函数与对数函数是高中阶段非常重要的基本初等函数,通过这两类重要的基本初等函数的学习,再次理解研究函数的基本方式,体会用函数模型解决问题的基本思路.
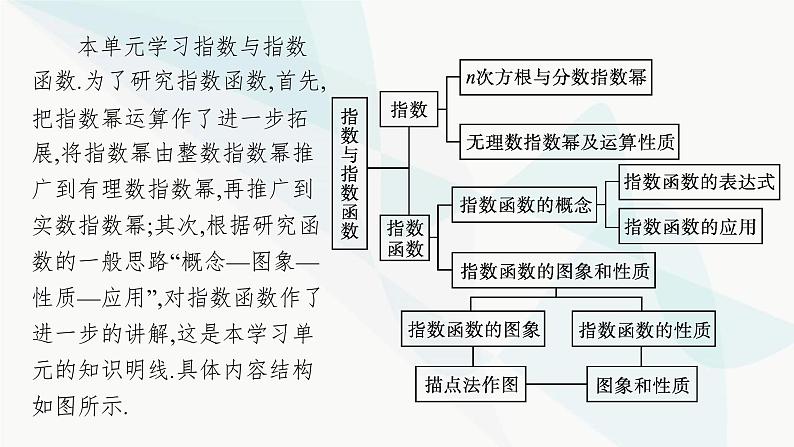
本单元学习指数与指数函数.为了研究指数函数,首先,把指数幂运算作了进一步拓展,将指数幂由整数指数幂推广到有理数指数幂,再推广到实数指数幂;其次,根据研究函数的一般思路“概念—图象—性质—应用”,对指数函数作了进一步的讲解,这是本学习单元的知识明线.具体内容结构如图所示.
本学习单元的最终目标就是掌握指数函数的图象性质,并能利用此函数模型解决问题.在此单元的学习过程中,通过指数运算、指数函数概念、指数函数图象及性质的学习,体会数形结合的思想方法,培养学生数学运算、数学抽象、直观想象、数学模型等核心素养.
知识点一:n次方根1.n次方根的定义:一般地,如果xn=a,那么x叫做　　　　　　,其中n>1,且n∈N*. 2.n次方根的性质(1)当n是奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数,这时,a的n次方根用符号 表示.(2)当n是偶数时,正数的n次方根有两个,这两个数互为相反数.这时正数a的正的n次方根用符号 表示,负的n次方根用符号　　　　表示.正的n次方根与负的n次方根可以合并写成　　　　　　　.负数没有偶次方根. (3)0的任何次方根都是0,记作　　　　　. 
3.根式的定义:式子 叫做根式,这里n叫做根指数,a叫做被开方数.(根号内的数)4.根式的性质:(1)( )n=a.
名师点睛1.在n次方根的概念中,关键是数a的n次方根x满足xn=a,因此求一个数a的n次方根,就是求一个数的n次方等于a.2.n次方根实际上就是平方根与立方根的推广.3.n次方根的概念表明,乘方与开方是互逆运算.
2.( )n中实数a的取值范围是任意实数吗?
提示 不一定,当n为大于1的奇数时,a∈R;当n为大于1的偶数时,a∈[0,+∞).
知识点二:分数指数幂1.正数的正分数指数幂的意义: (a>0,m,n∈N*,n>1).2.正数的负分数指数幂的意义:3.0的正分数指数幂等于0,0的负分数指数幂没有意义.规定了分数指数幂的意义以后,幂ax中指数x的取值范围就从整数拓展到了有理数.
名师点睛1.分数指数幂 不可理解为 个a相乘,它是根式的一种写法.2.正数的负分数指数幂总表示正数,而不是负数.3.我们可以类似得出:一般地,给定正数a,对任意无理数α,aα都是一个确定的实数.同理规定a-α= .这样指数幂中指数的范围就扩展到了全体实数.
知识点三:指数幂的运算性质对于任意正数a,b和实数r,s,指数幂均满足下面的运算性质:(1)aras=ar+s(a>0,r,s∈R);(2)(ar)s=ars(a>0,r,s∈R);(3)(ab)r=arbr(a>0,b>0,r∈R).名师点睛实数指数幂的运算性质除了上述三个外,还有如下两个常用性质:(1)ar÷as=ar-s(a>0,r,s∈R);
微思考为什么指数幂的运算法则要求a>0?
问题1我们知道,正数的平方根有两个,负数没有平方根.若将平方根推广至n次方根,类比初中平方根的定义,n次方根的定义是什么?被开方数需要满足什么条件?问题2根式与分数指数幂是如何转化的?认真探究问题: 一定相等吗?据此问题思考,根式与分数指数幂转化时需要特别注意什么?
探究点一 根式的概念
问题3根据根式的概念,如何区分求奇次方根与偶次方根?【例1】 (1)27的立方根是　　　　;16的4次方根是　　　. (2)已知x6=2 019,则x=　 　　. (3)若 有意义,则实数x的取值范围为　　　　　　　　　. 
规律方法　根式概念问题应关注的两点(1)n的奇偶性决定了n次方根的个数;(2)n为奇数时,被开方数a的正负决定着n次方根的符号.
探究点二 根式的化简(求值)
问题4根据根式的运算性质,如何对根式进行化简?【例2】 求下列各式的值:
解(1)原式=a-b+b-a=0.
∵-3