数学八年级上册13.3.2 等边三角形图文ppt课件

这是一份数学八年级上册13.3.2 等边三角形图文ppt课件，共20页。PPT课件主要包含了BC10cm，量一量，AB20cm，还有其他的方法吗，你能得出什么结论呢，符号语言表示，∵D是AB的中点，∵CD⊥AB，∴∠CDB90°，∴∠130°等内容，欢迎下载使用。

1、掌握含有30°角的直角三角形的性质和应用.2、探索并证明含有30°角的直角三角形性质的过程，并用以解决实际问题.
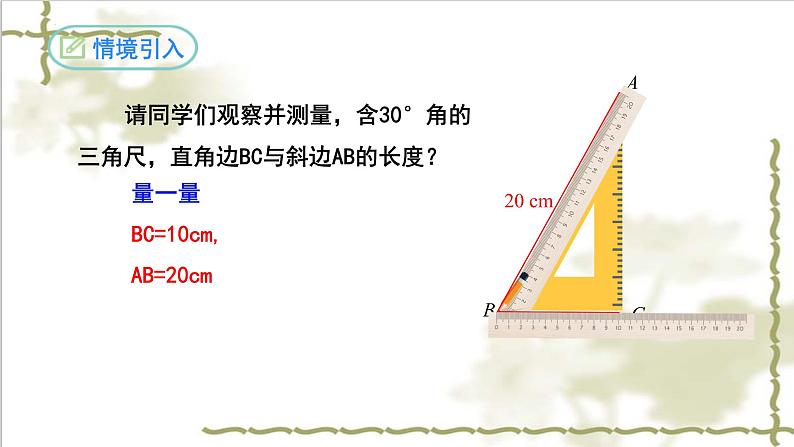
请同学们观察并测量，含30°角的三角尺，直角边BC与斜边AB的长度？
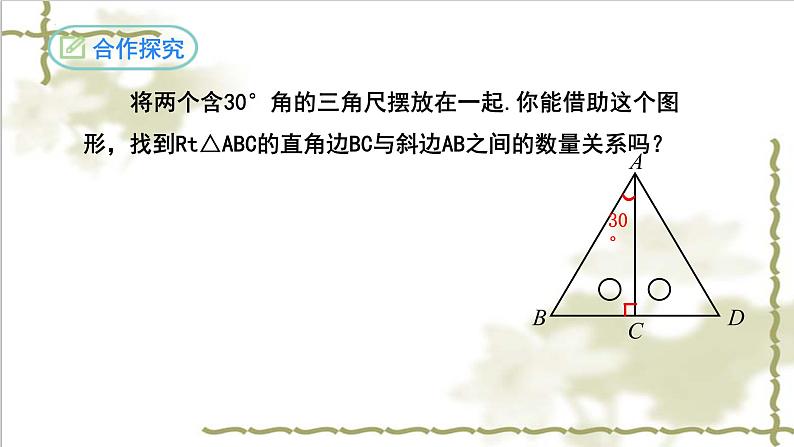
将两个含30°角的三角尺摆放在一起.你能借助这个图形，找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗？
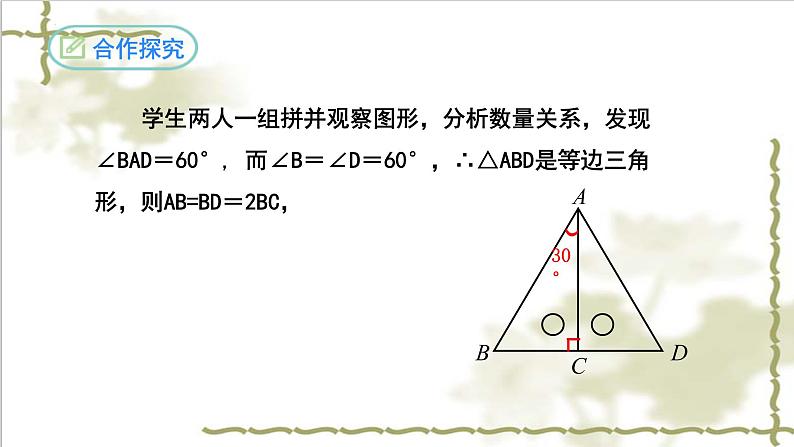
学生两人一组拼并观察图形，分析数量关系，发现∠BAD＝60°, 而∠B＝∠D＝60°，∴△ABD是等边三角形，则AB=BD＝2BC，
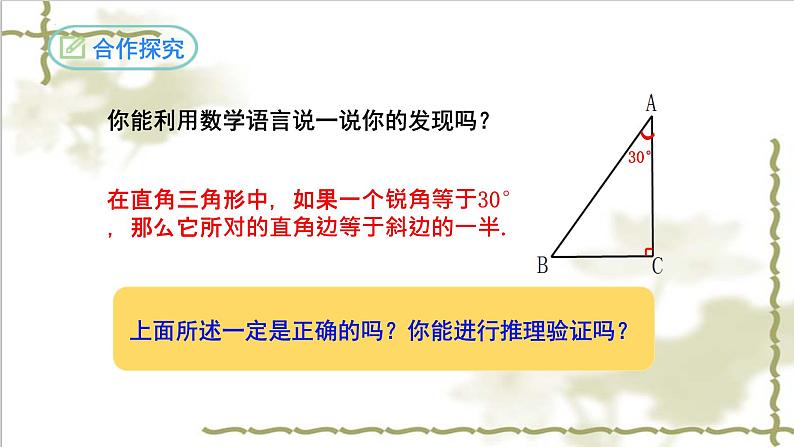
你能利用数学语言说一说你的发现吗？
在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
上面所述一定是正确的吗？你能进行推理验证吗？
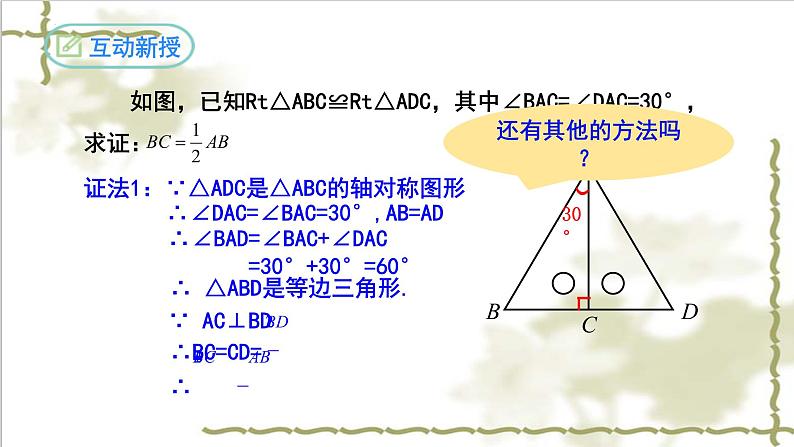
如图，已知Rt△ABC≌Rt△ADC，其中∠BAC=∠DAC=30°，求证：
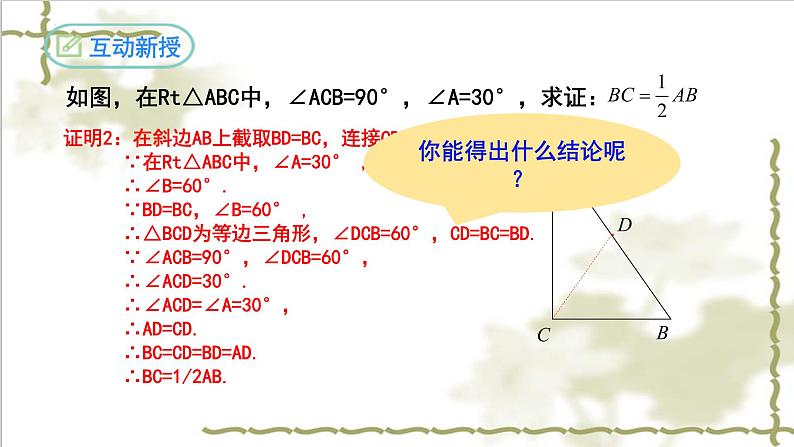
如图，在Rt△ABC中，∠ACB=90°，∠A=30°，求证：
证明2：在斜边AB上截取BD=BC，连接CD. ∵在Rt△ABC中，∠A=30° , ∴∠B=60°. ∵BD=BC，∠B=60° , ∴△BCD为等边三角形，∠DCB=60°，CD=BC=BD. ∵∠ACB=90°，∠DCB=60°， ∴∠ACD=30°. ∴∠ACD=∠A=30°， ∴AD=CD. ∴BC=CD=BD=AD. ∴BC=1/2AB.
在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.（简记为：30°的角所对的直角边等于斜边的一半）
含30°角的直角三角形的性质：
∵ ∠C=90°，∠A=30°
注意：必须满足两个条件
①30°的角，②直角三角形中.
例5:如图是屋架设计图的一部分，点D 是斜梁AB的中点，立柱BC、DE 垂直于横梁AC，AB =7.4 cm，∠A =30°，立柱BC、DE 要多长？
解：∵　BC⊥AC，∠A =30°
∵ DE⊥AC，∠A =30°
答：立柱BC 的长是3.7 m，DE 的长是1.85 m．　　
1．如图，在Rt△ABC中，∠A=30°，AB＋BC=12 cm，则AB= ．
2．如图：△ABC是等边三角形，AD⊥BC，DE⊥AB，若AB=8 cm，则BD= ，BE= ．
第1题 第2题
3.如图，在△ABC中，∠ACB=90°，BA的垂直平分线交边CB于D，若AB=10，AC=5，则图中等于30°的角的个数为（ ）．
A．2 B．3C．4 D．5
1.如图，已知△ABC中，AB=AC，∠C=30°，AB⊥AD，AD=4，求BC长。
解：在Rt△ABD中 ∵∠C=30° ∴BD=2AD=8 ∵∠BAD=90° 则∠DAC=∠C=30°，AD=CD=4 ∴BC=8+4=12
解：∵在△ABC中，∠C=90°，∠B=30°, ∴∠CAB=60°. ∵AD平分∠CAB, ∴∠CAD=∠BAD=30°. ∴∠B=∠BAD， ∴AD=BD. 在Rt△ACD中，∠C=90°， ∠CAD=30°，CD=2, ∴AD=2CD=4. ∴BD=AD=4.
2.如图，在△ABC中，∠C=90°，∠B=30°，AD平分∠CAB交BC于点D，若CD=2，求BD的长.
1.如图，在△ABC中，∠ACB=90°,CD是AB边上的高，∠A=30°，求证：AB=4BD.
解：∵∠ACB=90°, ∠A=30°
2.如图，一个等腰三角形的两个底角为15°，腰长为14cm，求这个等腰三角形的面积.
解：过点C作AB边上的高，交BA的延长线于点D. ∵∠B=∠ACB=15°， ∴∠DAC=30°. ∵AB=AC=14cm，CD⊥AB，∠DAC=30°， ∴CD=1/2AC=7cm. ∴S△ABC=1/2AB×CD=49cm2.
1．含30°角的直角三角形的性质：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．2．证明一条线段等于另一条线段一半或2倍的证明思路与方法：延长一倍或截半的方法将其转化为证明两条线段相等．
1.如图所示，在△ABC中，∠C=90°,∠B=15°,AB的垂直平分线交BC于点D,交AB于点M,BD=8cm,则AC=_______cm.
2.如图所示，在△ABC中，AB=AC=9,∠BAC=120°,AD是△ABC的中线，AE是∠BAD的平分线，DF//AB交AE的延长线于点F,则DF的长为_____.
第1题 第2题
3.如图，在Rt△ABC中，CD是斜边AB上的高，∠B=30°，CD=6cm，则BC的长度是多少？
解：∵CD是斜边AB边上的高， ∴∠BDC=90°. ∵在Rt△BCD中，∠B=30°，CD=6cm， ∴BC=2CD=12cm.