湖南省常德市2021-2023三年中考数学真题分类汇编-03解答题（基础题）知识点分类(含答案)

湖南省常德市2021-2023三年中考数学真题分类汇编-03解答题（基础题）知识点分类

一．实数的运算（共3小题）

1．（2023•常德）计算：．

2．（2022•常德）计算：30﹣（）﹣2sin30°+cos45°．

3．（2021•常德）计算：20210+3﹣1•﹣sin45°．

二．分式的混合运算（共2小题）

4．（2022•常德）化简：（a﹣1+）÷．

5．（2021•常德）化简：（+）÷．

三．分式的化简求值（共1小题）

6．（2023•常德）先化简，再求值：，其中x＝5．

四．解二元一次方程组（共1小题）

7．（2023•常德）解方程组：．

五．解一元二次方程-因式分解法（共1小题）

8．（2021•常德）解方程：x2﹣x﹣2＝0．

六．分式方程的应用（共1小题）

9．（2022•常德）小强的爸爸平常开车从家中到小强奶奶家，匀速行驶需要4小时．某天，他们以平常的速度行驶了的路程时遇到了暴雨，立即将车速减少了20千米/小时，到达奶奶家时共用了5小时，问小强家到他奶奶家的距离是多少千米？

七．一元一次不等式的应用（共1小题）

10．（2021•常德）某汽车贸易公司销售A、B两种型号的新能源汽车，A型车进货价格为每台12万元，B型车进货价格为每台15万元，该公司销售2台A型车和5台B型车，可获利3.1万元，销售1台A型车和2台B型车，可获利1.3万元．

（1）求销售一台A型、一台B型新能源汽车的利润各是多少万元？

（2）该公司准备用不超过300万元资金，采购A、B两种新能源汽车共22台，问最少需要采购A型新能源汽车多少台？

八．解一元一次不等式组（共1小题）

11．（2022•常德）解不等式组．

九．反比例函数系数k的几何意义（共1小题）

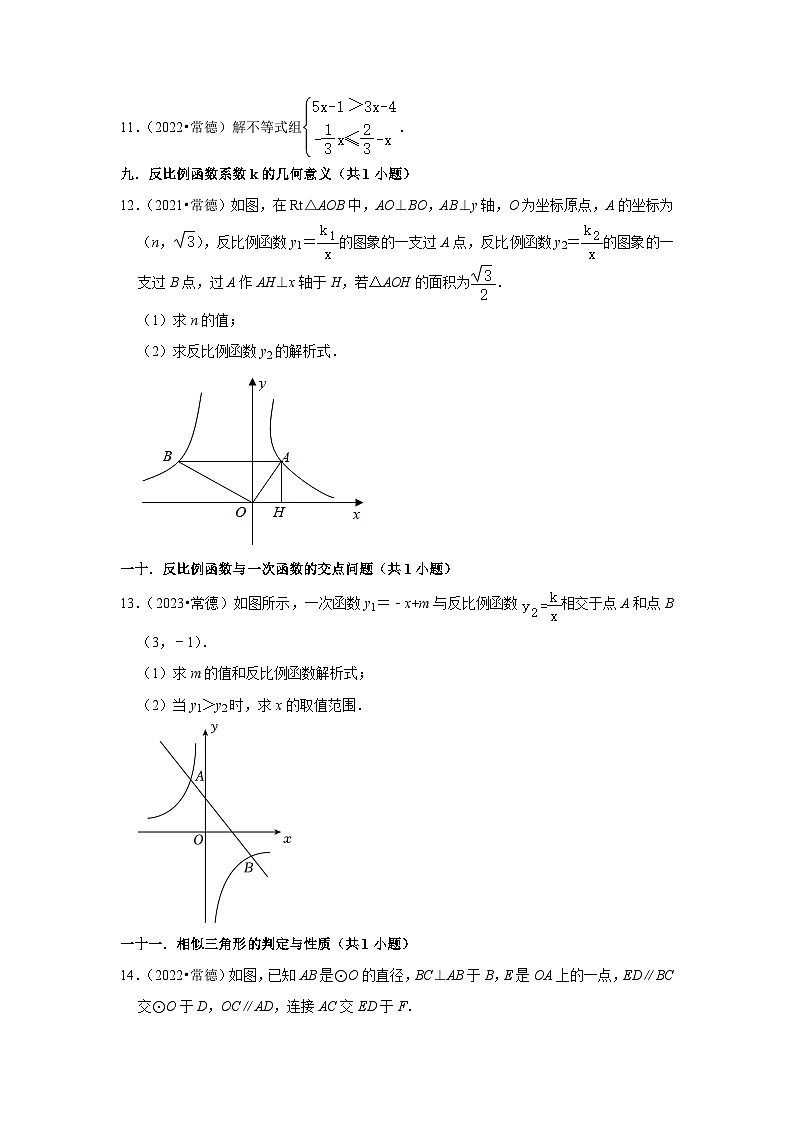
12．（2021•常德）如图，在Rt△AOB中，AO⊥BO，AB⊥y轴，O为坐标原点，A的坐标为（n，），反比例函数y1＝的图象的一支过A点，反比例函数y2＝的图象的一支过B点，过A作AH⊥x轴于H，若△AOH的面积为．

（1）求n的值；

（2）求反比例函数y2的解析式．

一十．反比例函数与一次函数的交点问题（共1小题）

13．（2023•常德）如图所示，一次函数y1＝﹣x+m与反比例函数相交于点A和点B（3，﹣1）．

（1）求m的值和反比例函数解析式；

（2）当y1＞y2时，求x的取值范围．

一十一．相似三角形的判定与性质（共1小题）

14．（2022•常德）如图，已知AB是⊙O的直径，BC⊥AB于B，E是OA上的一点，ED∥BC交⊙O于D，OC∥AD，连接AC交ED于F．

（1）求证：CD是⊙O的切线；

（2）若AB＝8，AE＝1，求ED，EF的长．

一十二．条形统计图（共1小题）

15．（2022•常德）2020年7月，教育部印发的《大中小学劳动教育指导纲要（试行）》中明确要求中小学劳动教育课平均每周不少于1课时，初中生平均每周劳动时间不少于3小时．某初级中学为了解学生劳动教育的情况，从本校学生中随机抽取了500名进行问卷调查．如图是根据此次调查结果得到的统计图．

请根据统计图回答下列问题：

（1）本次调查中，平均每周劳动时间符合教育部要求的人数占被调查人数的百分比为多少？

（2）若该校有2000名学生，请估计最喜欢的劳动课程为木工的有多少人．

（3）请你根据本次问卷调查的结果给同学和学校各提一条合理化建议．

一十三．中位数（共1小题）

16．（2023•常德）党的二十大报告指出：“我们要全方位夯实粮食安全根基，牢牢守住十八亿亩耕地红线．确保中国人的饭碗牢牢端在自己手中”．为了了解粮食生产情况，某校数学兴趣小组调查了某种粮大户2018年至2022年粮食总产量及2022年粮食分季节占比情况如下：

请根据图中信息回答下列问题：

（1）该种粮大户2022年早稻产量是 　     　吨；

（2）2018年至2022年该种粮大户粮食总产量的中位数是 　       　，平均数是 　       　；

（3）该粮食大户估计2023年的粮食总产量年增长率与2022年的相同，那么2023年该粮食大户的粮食总产量是多少吨？

湖南省常德市2021-2023三年中考数学真题分类汇编-03解答题（基础题）知识点分类

参考答案与试题解析

一．实数的运算（共3小题）

1．（2023•常德）计算：．

【答案】0．

【解答】解：原式＝1﹣2×+|1﹣|

＝1﹣+[﹣（1﹣）]

＝1﹣﹣（1﹣）

＝1﹣﹣1+

＝0．

2．（2022•常德）计算：30﹣（）﹣2sin30°+cos45°．

【答案】1．

【解答】解：30﹣（）﹣2sin30°+cos45°，

＝1﹣4×+2×，

＝1﹣2+2，

＝1．

故答案为：1．

3．（2021•常德）计算：20210+3﹣1•﹣sin45°．

【答案】1．

【解答】解：20210+3﹣1•﹣sin45°

＝1+×3﹣

＝1+1﹣1

＝1．

二．分式的混合运算（共2小题）

4．（2022•常德）化简：（a﹣1+）÷．

【答案】．

【解答】解：（a﹣1+）÷

＝[+]•

＝•

＝．

5．（2021•常德）化简：（+）÷．

【答案】．

【解答】解：（+）÷

＝[]

＝

＝

＝．

三．分式的化简求值（共1小题）

6．（2023•常德）先化简，再求值：，其中x＝5．

【答案】，．

【解答】解：

＝

＝

＝，

当x＝5时，

原式＝

＝．

四．解二元一次方程组（共1小题）

7．（2023•常德）解方程组：．

【答案】．

【解答】解：①×2+②得：5x＝25，

解得：x＝5，

将x＝5代入①得：5﹣2y＝1，

解得：y＝2，

所以原方程组的解是．

五．解一元二次方程-因式分解法（共1小题）

8．（2021•常德）解方程：x2﹣x﹣2＝0．

【答案】见试题解答内容

【解答】解：分解因式得：（x﹣2）（x+1）＝0，

可得x﹣2＝0或x+1＝0，

解得：x1＝2，x2＝﹣1．

六．分式方程的应用（共1小题）

9．（2022•常德）小强的爸爸平常开车从家中到小强奶奶家，匀速行驶需要4小时．某天，他们以平常的速度行驶了的路程时遇到了暴雨，立即将车速减少了20千米/小时，到达奶奶家时共用了5小时，问小强家到他奶奶家的距离是多少千米？

【答案】240千米．

【解答】解：设平常的速度是x千米/小时，

根据题意，得，

解得x＝60，

经检验，x＝60是原方程的根，

4×60＝240（千米），

答：小强家到他奶奶家的距离是240千米．

七．一元一次不等式的应用（共1小题）

10．（2021•常德）某汽车贸易公司销售A、B两种型号的新能源汽车，A型车进货价格为每台12万元，B型车进货价格为每台15万元，该公司销售2台A型车和5台B型车，可获利3.1万元，销售1台A型车和2台B型车，可获利1.3万元．

（1）求销售一台A型、一台B型新能源汽车的利润各是多少万元？

（2）该公司准备用不超过300万元资金，采购A、B两种新能源汽车共22台，问最少需要采购A型新能源汽车多少台？

【答案】（1）销售一台A型新能源汽车的利润是0.3万元，销售一台B型新能源汽车的利润是0.5万元；

（2）最少需要采购A型新能源汽车10台．

【解答】解：（1）设销售一台A型新能源汽车的利润是x万元，销售一台B型新能源汽车的利润是y万元，

依题意得：，

解得：．

答：销售一台A型新能源汽车的利润是0.3万元，销售一台B型新能源汽车的利润是0.5万元．

（2）设需要采购A型新能源汽车m台，则采购B型新能源汽车（22﹣m）台，

依题意得：12m+15（22﹣m）≤300，

解得：m≥10．

答：最少需要采购A型新能源汽车10台．

八．解一元一次不等式组（共1小题）

11．（2022•常德）解不等式组．

【答案】﹣＜x≤1．

【解答】解：由5x﹣1＞3x﹣4，得：x＞﹣，

由﹣≤﹣x，得：x≤1，

则不等式组的解集为﹣＜x≤1．

九．反比例函数系数k的几何意义（共1小题）

12．（2021•常德）如图，在Rt△AOB中，AO⊥BO，AB⊥y轴，O为坐标原点，A的坐标为（n，），反比例函数y1＝的图象的一支过A点，反比例函数y2＝的图象的一支过B点，过A作AH⊥x轴于H，若△AOH的面积为．

（1）求n的值；

（2）求反比例函数y2的解析式．

【答案】见试题解答内容

【解答】解：（1）S△AOH＝，

即，＝，

∴n＝1，

（2）过点B作BQ⊥x轴于点Q，如图所示：

∵AO⊥BO，AB⊥y轴，

∴∠OQB＝∠AHO＝∠AOB＝90°，

∴∠BOQ+∠AOH＝90°，∠AOH+∠OAH＝90°，

∴∠BOQ＝∠OAH，

∴△BOQ∽△OAH，且BQ＝AH＝，

∴，即，

∴QO＝3，

∵点B位于第二象限，

∴点B的坐标（﹣3，），

将点B的坐标代入反比例函数y2＝中，

k2＝﹣3×＝﹣3，

∴反比例函数y2的解析式为：y2＝﹣．

一十．反比例函数与一次函数的交点问题（共1小题）

13．（2023•常德）如图所示，一次函数y1＝﹣x+m与反比例函数相交于点A和点B（3，﹣1）．

（1）求m的值和反比例函数解析式；

（2）当y1＞y2时，求x的取值范围．

【答案】（1）m＝2，反比例函数的解析式为y2＝﹣；

（2）x＜﹣1或0＜x＜3．

【解答】解：（1）∵一次函数y1＝﹣x+m与反比例函数相交于点A和点B（3，﹣1），

∴﹣1＝﹣3+m，﹣1＝，

解得m＝2，k＝﹣3，

∴反比例函数的解析式为y2＝﹣；

（2）解方程组，得或，

∴A（﹣1，3），

观察图象可得，当y1＞y2时，x的取值范围为x＜﹣1或0＜x＜3．

一十一．相似三角形的判定与性质（共1小题）

14．（2022•常德）如图，已知AB是⊙O的直径，BC⊥AB于B，E是OA上的一点，ED∥BC交⊙O于D，OC∥AD，连接AC交ED于F．

（1）求证：CD是⊙O的切线；

（2）若AB＝8，AE＝1，求ED，EF的长．

【答案】（1）证明见解答过程；

（2），．

【解答】（1）证明：连接OD，

∵AD∥OC，

∴∠BOC＝∠OAD，∠DOC＝∠ODA，

∵OA＝OD，

∴∠OAD＝∠ODA，

∴∠BOC＝∠DOC，

在△BOC和△DOC中，

，

∴△BOC≌△DOC（SAS），

∴∠ODC＝∠OBC＝90°，

∵OD为⊙O的半径，

∴CD是⊙O的切线；

（2）解：过点D作DH⊥BC于H，

∵ED∥BC，

∴∠OED＝180°﹣∠ABC＝90°，

则四边形EBHD为矩形，

∴BH＝ED，DH＝BE＝7，

∵AB＝8，AE＝1，

∴OE＝3，

∴ED＝＝＝，

∵CB、CD是⊙O的切线

∴CB＝CD，

设CB＝CD＝x，则CH＝x﹣，

在Rt△DHC中，DH2+CH2＝CD2，即72+（x﹣）2＝x2，

解得：x＝4，即BC＝4，

∵ED∥BC，

∴＝，即＝，

解得：EF＝．

一十二．条形统计图（共1小题）

15．（2022•常德）2020年7月，教育部印发的《大中小学劳动教育指导纲要（试行）》中明确要求中小学劳动教育课平均每周不少于1课时，初中生平均每周劳动时间不少于3小时．某初级中学为了解学生劳动教育的情况，从本校学生中随机抽取了500名进行问卷调查．如图是根据此次调查结果得到的统计图．

请根据统计图回答下列问题：

（1）本次调查中，平均每周劳动时间符合教育部要求的人数占被调查人数的百分比为多少？

（2）若该校有2000名学生，请估计最喜欢的劳动课程为木工的有多少人．

（3）请你根据本次问卷调查的结果给同学和学校各提一条合理化建议．

【答案】（1）21%；

（2）320人；

（3））（答案不唯一，合理即可）如：建议学生积极参加学校的劳动课程，多做家务等等；建议学校增设特色劳动课程，增加劳动课的课时等．

【解答】解：（1）×100%＝21%，

∴本次调查中，平均每周劳动时间符合教育部要求的人数占被调查人数的百分比为21%；

（2）2000×（1﹣40%﹣27%﹣7%﹣10%）＝320（人），

∴若该校有2000名学生，则最喜欢的劳动课程为木工的估计有320人；

（3）（答案不唯一，合理即可）

如：建议学生积极参加学校的劳动课程，多做家务等等；建议学校增设特色劳动课程，增加劳动课的课时等．

一十三．中位数（共1小题）

16．（2023•常德）党的二十大报告指出：“我们要全方位夯实粮食安全根基，牢牢守住十八亿亩耕地红线．确保中国人的饭碗牢牢端在自己手中”．为了了解粮食生产情况，某校数学兴趣小组调查了某种粮大户2018年至2022年粮食总产量及2022年粮食分季节占比情况如下：

请根据图中信息回答下列问题：

（1）该种粮大户2022年早稻产量是 　10　吨；

（2）2018年至2022年该种粮大户粮食总产量的中位数是 　160吨　，平均数是 　174吨　；

（3）该粮食大户估计2023年的粮食总产量年增长率与2022年的相同，那么2023年该粮食大户的粮食总产量是多少吨？

【答案】（1）10；

（2）160吨；174吨；

（3）312.5吨．

【解答】解：（1）250×（1﹣75%﹣21%）＝10（吨）．

故答案为：10；

（2）将5个数据按从小到大的顺序排列后，第三个数为160，所以中位数为160吨；

＝（120+140+160+200+250）÷5＝174（吨）．

故答案为：160吨；174吨；

（3）（250﹣200）÷200×100%＝25%，

250×（1+25%）＝312.5（吨）．

即2023年该粮食大户的粮食总产量是312.5吨．