湖南省娄底市2021-2023三年中考数学真题分类汇编-03解答题（基础题）知识点分类

湖南省娄底市2021-2023三年中考数学真题分类汇编-03解答题（基础题）知识点分类

一．实数的运算（共2小题）

1．（2023•娄底）计算：（π﹣2023）0+|1﹣|+﹣tan60°．

2．（2022•娄底）计算：（2022﹣π）0+（）﹣1+|1﹣|﹣2sin60°．

二．分式的化简求值（共2小题）

3．（2022•娄底）先化简，再求值：（x+2+）÷，其中x是满足条件x≤2的合适的非负整数．

4．（2021•娄底）先化简，再求值：•（1﹣），其中x是1、2、3中的一个合适的数．

三．分母有理化（共1小题）

5．（2021•娄底）计算：（﹣π）0++（）﹣1﹣2cos45°．

四．二元一次方程组的应用（共1小题）

6．（2021•娄底）为了庆祝中国共产党建党一百周年，某校举行“礼赞百年，奋斗有我”演讲比赛，准备购买甲、乙两种纪念品奖励在活动中表现优秀的学生．已知购买1个甲种纪念品和2个乙种纪念品共需20元，购买2个甲种纪念品和5个乙种纪念品共需45元．

（1）求购买一个甲种纪念品和一个乙种纪念品各需多少元；

（2）若要购买这两种纪念品共100个，投入资金不少于766元又不多于800元，问有多少种购买方案？并求出所花资金的最小值．

五．一元一次不等式的应用（共1小题）

7．（2023•娄底）为落实“五育并举”，绿化美化环境，学校在劳动周组织学生到校园周边种植甲、乙两种树苗，已知购买甲种树苗3棵，乙种树苗2棵共需12元；购买甲种树苗1棵，乙种树苗3棵共需11元．

（1）求每棵甲、乙树苗的价格；

（2）本次活动共种植了200棵甲、乙树苗，假设所种的树苗若干年后全部长成了参天大树，并且平均每棵树的价值（含生态价值、经济价值等）均为原来树苗价的100倍，要想获得不低于5万元的价值，请问乙种树苗种植数量不得少于多少棵？

六．切线的判定与性质（共1小题）

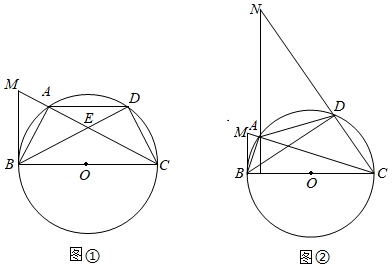
8．（2021•娄底）如图，点A在以BC为直径的⊙O上，∠ABC的角平分线与AC相交于点E，与⊙O相交于点D，延长CA至M，连结BM，使得MB＝ME，过点A作BM的平行线与CD的延长线交于点N．

（1）求证：BM与⊙O相切；

（2）试给出AC、AD、CN之间的数量关系，并予以证明．

七．解直角三角形的应用（共1小题）

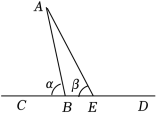
9．（2023•娄底）几位同学在老师的指导下到某景区进行户外实践活动，在登山途中发现该景区某两座山之间风景优美，但路陡难行，为了便于建议景区管理处在这两山顶间建观光索道，他们分别在两山顶上取A、B两点，并过点B架设一水平线型轨道CD（如图所示），使得∠ABC＝α，从点B出发按CD方向前进20米到达点E，即BE＝20米，测得∠AEB＝β，已知sinα＝，tanβ＝3，求A、B两点间的距离．

八．条形统计图（共3小题）

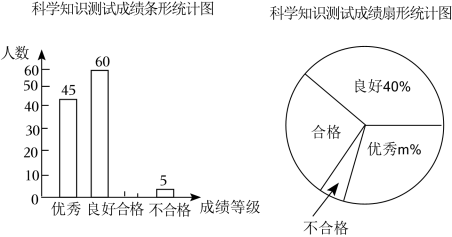
10．（2023•娄底）某区教育局为了了解某年级学生对科学知识的掌握情况，在全区范围内随机抽取若干名个学生进行科学知识测试，按照测试成绩分优秀，良好、合格与不合格四个等级，并绘制了如图所示两幅不完整统计图．

（1）参与本次测试的学生人数为 　      　，m＝　     　；

（2）请补全条形统计图；

（3）若全区该年级共有5000名学生，请估计该年级对科学知识掌握情况较好（测试成绩能达到良好及以上等级）的学生人数．

​

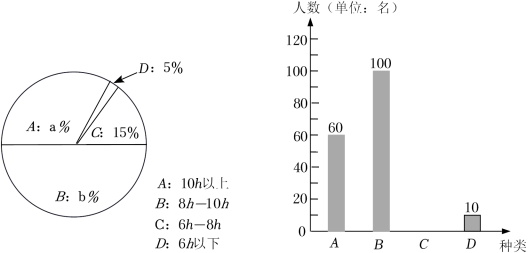
11．（2022•娄底）按国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》要求，各中小学校积极行动，取得了良好的成绩．某中学随机抽取了部分学生对他们一周的课外阅读时间（A：10h以上，B：8h～10h，C：6h～8h，D：6h以下）进行问卷调查，将所得数据进行分类，统计绘制了如下不完整的统计图．请根据图中的信息，解答下列问题：

（1）本次调查的学生共 　      　名；

（2）a＝　     　，b＝　     　；

（3）补全条形统计图．

12．（2021•娄底）“读书，点亮未来”，广泛的课外阅读是同学们搜集和汲取知识的一条重要途径．学校图书馆计划购进一批学生喜欢的图书，为了了解学生们对“A文史类、B科普类、C生活类、D其它”的喜欢程度，随机抽取了部分学生进行问卷调查（每个学生只选其中一类），将所得数据进行分类统计绘制了不完整的统计图表，请根据图中的信息，解答下列问题：

统计表：

（1）本次调查的学生共 　      　人；

（2）m＝　       　，n＝　     　；

（3）补全条形统计图．

湖南省娄底市2021-2023三年中考数学真题分类汇编-03解答题（基础题）知识点分类

参考答案与试题解析

一．实数的运算（共2小题）

1．（2023•娄底）计算：（π﹣2023）0+|1﹣|+﹣tan60°．

【答案】2．

【解答】解：原式＝1+﹣1+2﹣＝2．

2．（2022•娄底）计算：（2022﹣π）0+（）﹣1+|1﹣|﹣2sin60°．

【答案】2．

【解答】解：原式＝1+2+﹣1﹣2×

＝1+2+﹣1﹣

＝2．

二．分式的化简求值（共2小题）

3．（2022•娄底）先化简，再求值：（x+2+）÷，其中x是满足条件x≤2的合适的非负整数．

【答案】，﹣1．

【解答】解：原式＝（+）÷

＝•

＝，

∵x≠0且x﹣2≠0，

∴x≠0且x≠2，

∴x＝1，

则原式＝＝﹣1．

4．（2021•娄底）先化简，再求值：•（1﹣），其中x是1、2、3中的一个合适的数．

【答案】，．

【解答】解：原式＝•

＝•

＝，

由题意得：x≠1，x≠±3，

当x＝2时，原式＝＝．

三．分母有理化（共1小题）

5．（2021•娄底）计算：（﹣π）0++（）﹣1﹣2cos45°．

【答案】2．

【解答】解：原式＝1++2﹣2×

＝1+﹣1+2﹣

＝2．

四．二元一次方程组的应用（共1小题）

6．（2021•娄底）为了庆祝中国共产党建党一百周年，某校举行“礼赞百年，奋斗有我”演讲比赛，准备购买甲、乙两种纪念品奖励在活动中表现优秀的学生．已知购买1个甲种纪念品和2个乙种纪念品共需20元，购买2个甲种纪念品和5个乙种纪念品共需45元．

（1）求购买一个甲种纪念品和一个乙种纪念品各需多少元；

（2）若要购买这两种纪念品共100个，投入资金不少于766元又不多于800元，问有多少种购买方案？并求出所花资金的最小值．

【答案】（1）购买一个甲种纪念品需要10元，购买一个乙种纪念品需要5元；

（2）共有7种购买方案，所花资金的最小值为770元．

【解答】解：（1）设购买一个甲种纪念品需要x元，购买一个乙种纪念品需要y元，

依题意得：，

解得：．

答：购买一个甲种纪念品需要10元，购买一个乙种纪念品需要5元．

（2）设购买m个甲种纪念品，则购买（100﹣m）个乙种纪念品，

依题意得：，

解得：53≤m≤60，

又∵m为整数，

∴m可以为54，55，56，57，58，59，60，

∴共有7种购买方案．

设购买总费用为w元，则w＝10m+5（100﹣m）＝5m+500，

∵5＞0，

∴w随m的增大而增大，

∴当m＝54时，w取得最小值，最小值＝5×54+500＝770．

答：共有7种购买方案，所花资金的最小值为770元．

五．一元一次不等式的应用（共1小题）

7．（2023•娄底）为落实“五育并举”，绿化美化环境，学校在劳动周组织学生到校园周边种植甲、乙两种树苗，已知购买甲种树苗3棵，乙种树苗2棵共需12元；购买甲种树苗1棵，乙种树苗3棵共需11元．

（1）求每棵甲、乙树苗的价格；

（2）本次活动共种植了200棵甲、乙树苗，假设所种的树苗若干年后全部长成了参天大树，并且平均每棵树的价值（含生态价值、经济价值等）均为原来树苗价的100倍，要想获得不低于5万元的价值，请问乙种树苗种植数量不得少于多少棵？

【答案】见试题解答内容

【解答】解：（1）设甲种树苗的价格为x元/棵，乙种树苗的价格为y元/棵，

根据题意得：，

解得：．

答：甲种树苗的价格为2元/棵，乙种树苗的价格为3元/棵；

（2）设种植乙种树苗m棵，则种植甲种树苗（200﹣m）棵，

根据题意得：2×100（200﹣m）+3×100m≥50000，

解得：m≥100，

∴m的最小值为100．

答：乙种树苗种植数量不得少于100棵．

六．切线的判定与性质（共1小题）

8．（2021•娄底）如图，点A在以BC为直径的⊙O上，∠ABC的角平分线与AC相交于点E，与⊙O相交于点D，延长CA至M，连结BM，使得MB＝ME，过点A作BM的平行线与CD的延长线交于点N．

（1）求证：BM与⊙O相切；

（2）试给出AC、AD、CN之间的数量关系，并予以证明．

【答案】（1）证明见解析过程；

（2）AC2＝CN•AD，理由见解析过程．

【解答】证明：（1）∵BC是直径，

∴∠BAC＝90°，

∴∠ABE+∠AEB＝90°，

∵BD平分∠ABC，

∴∠ABD＝∠DBC，

∵MB＝ME，

∴∠MBE＝∠MEB，

∴∠MBE+∠EBC＝90°，

∴∠MBC＝90°，

∴MB⊥BC，

∴BM与⊙O相切；

（2）AC2＝CN•AD，

理由如下：∵∠ACD＝∠ABD，∠DBC＝∠DAC，

∴∠DCA＝∠DAC，

∴AD＝DC，

∵BC是直径，

∴∠BDC＝90°，

∴∠BCD+∠DBC＝90°，

∵AN∥BM，BM⊥BC，

∴AN⊥BC，

∴∠N+∠DCB＝90°，

∴∠N＝∠DBC，

∴∠N＝∠DBC＝∠DCA＝∠DAC，

∴△DAC∽△ANC，

∴，

∴AC2＝CN•AD．

七．解直角三角形的应用（共1小题）

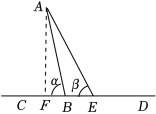
9．（2023•娄底）几位同学在老师的指导下到某景区进行户外实践活动，在登山途中发现该景区某两座山之间风景优美，但路陡难行，为了便于建议景区管理处在这两山顶间建观光索道，他们分别在两山顶上取A、B两点，并过点B架设一水平线型轨道CD（如图所示），使得∠ABC＝α，从点B出发按CD方向前进20米到达点E，即BE＝20米，测得∠AEB＝β，已知sinα＝，tanβ＝3，求A、B两点间的距离．

【答案】A、B两点间的距离为500米．

【解答】解：过点A作AF⊥CD于点F，

∴∠AFB＝90°，

在Rt△ABF中，，

∴设AF＝24x米，AB＝25x米，

则由勾股定理得米，

在Rt△AFE中，，

∵BE＝20米，

∴，

解得x＝20，

∴AB＝25x＝500米．

答：A、B两点间的距离为500米．

八．条形统计图（共3小题）

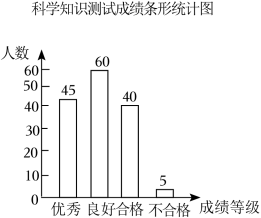
10．（2023•娄底）某区教育局为了了解某年级学生对科学知识的掌握情况，在全区范围内随机抽取若干名个学生进行科学知识测试，按照测试成绩分优秀，良好、合格与不合格四个等级，并绘制了如图所示两幅不完整统计图．

（1）参与本次测试的学生人数为 　150　，m＝　30　；

（2）请补全条形统计图；

（3）若全区该年级共有5000名学生，请估计该年级对科学知识掌握情况较好（测试成绩能达到良好及以上等级）的学生人数．

​

【答案】（1）150，30；

（2）详见解答；

（3）3500．

【解答】解：（1）60÷40%＝150（人），

45÷150×100%＝30%，即m＝30，

故答案为：150，30；

（2）样本中成绩为“合格”的学生人数为150﹣45﹣60﹣5＝40（人），补全条形统计图如下：

（3）5000×＝3500（人），

答：全区该年级5000名学生中对科学知识掌握情况较好（测试成绩能达到良好及以上等级）的学生人数大约有3500人．

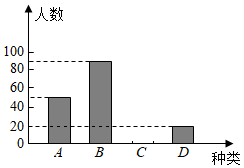
11．（2022•娄底）按国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》要求，各中小学校积极行动，取得了良好的成绩．某中学随机抽取了部分学生对他们一周的课外阅读时间（A：10h以上，B：8h～10h，C：6h～8h，D：6h以下）进行问卷调查，将所得数据进行分类，统计绘制了如下不完整的统计图．请根据图中的信息，解答下列问题：

（1）本次调查的学生共 　200　名；

（2）a＝　30　，b＝　50　；

（3）补全条形统计图．

【答案】（1）200；

（2）30，50；

（3）补全条形统计图见解析．

【解答】解：（1）本次调查的学生共：10÷5%＝200（名），

故答案为：200；

（2）a＝×100＝30，b＝×100＝50，

故答案为：30，50；

（3）C类人数为200×15%＝30，

补全条形统计图如图：

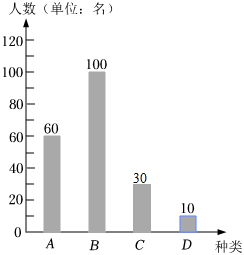
12．（2021•娄底）“读书，点亮未来”，广泛的课外阅读是同学们搜集和汲取知识的一条重要途径．学校图书馆计划购进一批学生喜欢的图书，为了了解学生们对“A文史类、B科普类、C生活类、D其它”的喜欢程度，随机抽取了部分学生进行问卷调查（每个学生只选其中一类），将所得数据进行分类统计绘制了不完整的统计图表，请根据图中的信息，解答下列问题：

统计表：

（1）本次调查的学生共 　200　人；

（2）m＝　0.25　，n＝　40　；

（3）补全条形统计图．

【答案】（1）200；（2）0.25，40；（3）见解析．

【解答】解：（1）20÷0.10＝200（人），

故答案为：200；

（2）m＝50÷200＝0.25，n＝200×0.20＝40，

故答案为：0.25，40；

（3）补全条形统计图如下，