初中数学北师大版九年级下册第三章 圆8 圆内接正多边形教课课件ppt

这是一份初中数学北师大版九年级下册第三章 圆8 圆内接正多边形教课课件ppt，共13页。PPT课件主要包含了情景引入，探索新知，圆心角，扇形的定义，想一想，例题学习，归纳总结等内容，欢迎下载使用。
在一块空旷的草地上有一根柱子，柱子上拴着一条长3m的绳子，绳子的一端拴着一只狗。（1）这只狗的最大活动区域有多大？这个区域的边缘长是多少？（2）如果这只狗拴在夹角为120°的墙角 ，那么它的最大活动区域有多大？这个区域的边缘长是多少？
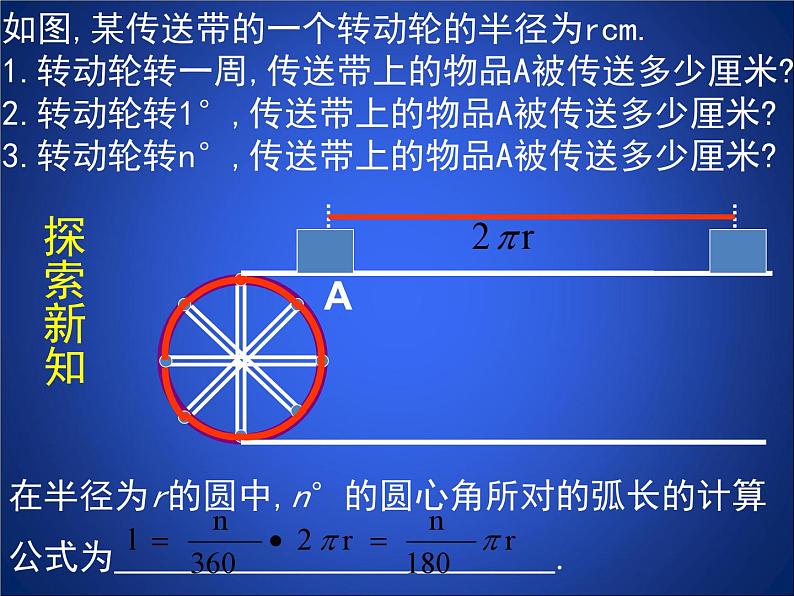
如图,某传送带的一个转动轮的半径为rcm.1.转动轮转一周,传送带上的物品A被传送多少厘米?2.转动轮转1°,传送带上的物品A被传送多少厘米?3.转动轮转n°,传送带上的物品A被传送多少厘米?
在半径为r的圆中,n°的圆心角所对的弧长的计算公式为 .
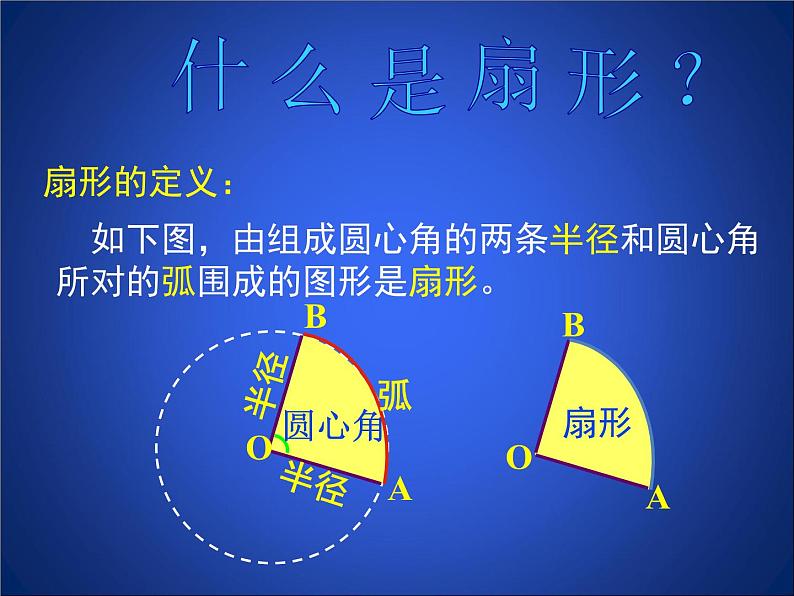
什 么 是 扇 形 ？
如下图，由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
如 何 求 扇 形 的 面 积 ？
扇形面积的大小到底和哪些因素有关呢？
（当圆半径一定时）扇形的面积随着圆心角的增大而增大。
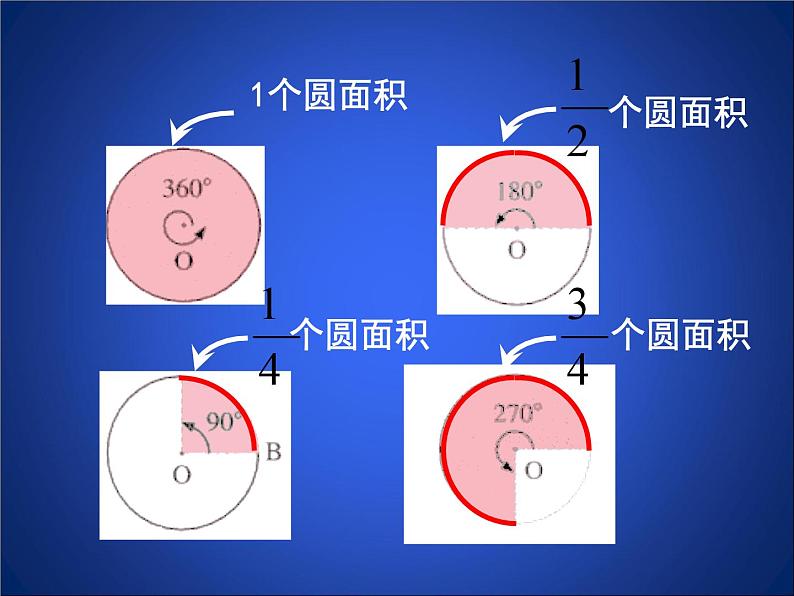
1. 圆心角是3600的扇形面积是多少？
2. 圆心角是1800的扇形面积是多少？
3. 圆心角是900的扇形面积是多少？
4. 圆心角是2700的扇形面积是多少？
圆心角是10的扇形面积是多少？
圆心角为n0的扇形面积是多少?
圆心角是n0的扇形面积是圆面积的n/360
如果用字母 S 表示扇形的面积，n表示圆心角的度数，r 表示圆半径，那么扇形面积的计算公式是：
例1 制作弯形管道时,需要先按中心计算“展开长度”再下料.试计算图所示的管道的展直长度,即弧AB的长(结果精确到0.1mm).
课本P100页 想一想
例2 扇形AOB的半径为12cm, ∠AOB=120°,求AB的长(结果精确到0.1cm)和扇形AOB的面积(结果精确到0.1cm2)。
问题1：比较扇形面积与弧长公式, 你能用弧长表示扇形面积吗？
扇形面积与弧长公式联系
弧长与圆的周长有关，扇形的面积与圆的面积有关。因此，计算弧长是 ;而计算扇形的面积时是 .