- 【小单元教案】高中数学人教A版(2019)必修第一册--5.2.2 同角三角函数的基本关系(第3课时)(课时教学设计3) 教案 2 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--5.3 诱导公式(单元教学设计) 教案 3 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--5.3.2 诱导公式的应用(第2课时)(课时教学设计) 教案 2 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--5.4 三角函数的图象与性质(单元教学设计) 教案 2 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--5.4.1 正弦函数、余弦函数的图像(第1课时)(课时教学设计) 教案 2 次下载
高中数学人教A版 (2019)必修 第一册第五章 三角函数5.3 诱导公式一等奖第1课时教学设计
展开![]() 课题:5.3.1 诱导公式(第1课时)
课题:5.3.1 诱导公式(第1课时)
(一)教学内容
诱导公式二~四(π±α,-α的正弦、余弦和正切).
(二)教学目标
1、从三角函数的定义出发,借助单位圆关于原点的对称性,能推导π+α的正弦、余弦和正切,发展直观想象、逻辑推理素养.
2、通过类比公式二的推导过程,能自主探究-α,π-α的正弦、余弦和正切,得出公式三、公式四,获得基本思想,积累基本活动经验.
3、通过建立公式一~四之间的联系,能利用公式将任意角的三角函数转化为锐角三角函数,会用公式一~四进行简单三角函数式的化简求值,发展数学运算的素养.
(三)教学重点及难点:
1、重点
利用圆的对称性探究诱导公式二~四.
2、难点
建立单位圆的对称性与π+α的正弦、余弦和正切之间的联系.
(四)教学过程设计
问题1:(1)回顾任意角三角函数的定义、公式一、同角三角函数的基本关系式,并回顾它们的研究方法.
(2)回答下列问题:
①点![]() 关于坐标原点的对称点
关于坐标原点的对称点![]() 的坐标是什么?
的坐标是什么?
②写出与点![]() 有如下对称性的点的坐标:关于原点对称的点 ,关于x轴对称的点 ,关于y轴对称的点 .
有如下对称性的点的坐标:关于原点对称的点 ,关于x轴对称的点 ,关于y轴对称的点 .
师生活动:对于(1)教师引导学生回顾任意角三角函数的定义、公式一、同角三角函数的基本关系式,并总结研究方法:借助于单位圆,利用圆的一些几何性质来研究.对于(2)学生完成,有问题及时解决.
设计意图:通过(1)回顾之前学习过的相关知识,为提出新问题做好铺垫,通过(2)检查学生对直角坐标系中具有特殊对称关系的两个点的坐标间的关系的掌握情况,为得到公式二~四做好准备.
问题2:前面我们从三角函数的定义出发,研究了终边相同的角的三角函数之间的关系,你认为接下来应该研究什么呢?
师生活动:学生可能会想到研究终边不相同的角的三角函数值之间的关系.教师追问:任意两个终边不相同的角的三角函数值之间有什么确定的关系吗?学生能够想到任意两个终边不相同的角的三角函数值之间是没有确定的关系的.教师继续追问:当两个角的终边有某些特殊的位置关系时,它们的三角函数值之间会不会就具有一定的关系了?你认为可以研究具有什么样的特殊位置关系的两个角的三角函数值之间的关系呢?学生可能会想到研究终边关于原点、x轴、y轴对称的角的三角函数值之间的关系.教师继续追问:可以想到研究三角函数值之间的关系要从定义出发,进而引出单位圆,而且圆也具有对称性,恰好与我们要研究的问题契合.进而学生可想到如下方法:
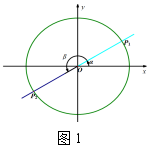
如图1,在直角坐标系内,设任意角α的终边与单位圆交于点P1,作P1关于原点的对称点P2
(1)以OP2为终边的角β与角α有什么关系?
(2)角β,α的三角函数值之间有什么关系?
 师生活动:
师生活动:
第一步,先从形上找到角之间的关系:以OP2为终边的角β都是与角π+α
终边相同的角,即β=2kπ+(π+α)(k∈Z).
第二步,建立关于原点对称的点的坐标之间的关系,将形的关系代数化:
设P1(x1,y1),P2(x2,y2).因为P2,P1关于原点对称,所以x2=-x1,y2=-y1.
第三步,等量代换数得到三角函数值之间的关系:由三角函数的定义得
sin α=y1,cos α=x1,tan α=(x1≠0);sin(π+α)=y2,cos(π+α)=x2,tan(π+α)=(x2≠0).
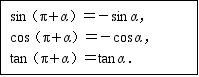 从而得 公式二:
从而得 公式二:
追问1:问题中给出的α是任意角,而我们图中的α为第一象限角,我们得到的结论适用于任意角吗?
师生活动:学生思考、讨论得出:无论α的终边在什么位置,点P1、P2关于原点对称的位置关系不变,因此坐标间的关系也不变,π+α与α的三角函数值的关系就不会改变.
追问2:归纳推导公式二的过程,你能给出主要的研究路径吗?
师生活动:学生思考、交流后得出研究路径:
单位圆的对称性→角与角的关系→对称点的坐标间的关系→三角函数值之间的关系.
设计意图:在探究过程中,引导学生从三角函数定义出发,使他们认识到可以利用圆的对称性研究三角函数的性质,感受由形到数的转化,感悟数形结合的思想方法,提升直观想象素养.带领学生梳理研究路径,进一步明确研究的方向和步骤,为后续的自主探究打下基础.
问题2:类比公式二的探究过程,借助于平面直角坐标系,你认为还需要研究点P1的哪些特殊的对称点?又能得出怎样的结论呢?
师生活动:学生可以自然地发现还需要研究点P1关于x轴、y轴对称的点.通过自主探究、小组讨论,教师巡视观察,适时引导.大多数学生可以独立完成公式三、四的推导.

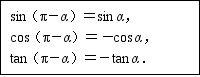
公式三: 公式四:
设计意图:将角的终边关于坐标轴对称时的三角函数关系一起让学生探究,既突出了诱导公式的整体研究架构,又检验了学生对公式二的学习效果,提升学生的逻辑推理素养.
问题3:例1 利用公式求下列三角函数值:
(1)cos 225°;(2)sin![]() ;(3)sin
;(3)sin![]() ;(4)tan(-2 040°).
;(4)tan(-2 040°).
追问1:题目中的角与哪个特殊角接近?应该选择哪个诱导公式化简求值?
师生活动:学生独立完成之后展示交流,注意展示其思考过程,教师帮助规范求解过程.
(1)cos 225°=cos(180°+45°)=-cos 45°=-![]() ;
;
(2)sin![]() =sin
=sin![]() =sin
=sin![]() =sin
=sin![]() =sin
=sin![]() =
=![]() ;
;
(3)sin![]() =-sin
=-sin![]() =-sin
=-sin![]() =
=![]() =
=![]() ;
;
(4)tan(-2 040°)=-tan 2 040° =-tan(6×360°-120°)=tan 120°=tan(180°-60°)=-tan 60°=-![]() .
.
追问2:通过上面四个题目的解答,你对公式一~公式四的作用有什么进一步的认识?你能归纳一下把任意角的三角函数转化为锐角的三角函数的步骤吗?
师生活动:先由学生阐述自己的想法,老师带领学生一起总结:
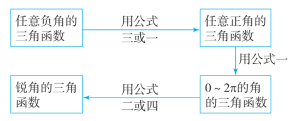
例2 化简:.
追问3:本题与例1的区别是什么?由例1总结出的求解步骤还能用吗?
师生活动:区别:例1涉及的是具体的角而例2用的是抽象的角α,求解步骤依然适用.学生独立完成,展示交流,注意展示其思考过程,教师帮助规范求解过程.
tan(-α-180°)=tan[-(180°+α)]=-tan(180°+α)=-tanα,
cos(-180°+α)=cos[-(180°-α)]=cos(180°-α)=-cos α,
所以,原式==-cos α.
设计意图:让学生在自主选择公式求解问题的过程中,体会公式一~公式四各自的作用,总结根据题目的条件选择公式的方法和步骤,形成程序化的解题步骤,体会算法思想、转化与化归的思想,发展数学运算的素养.
问题4:回忆本节课的学习内容,回答下面的问题:
(1)我们是如何发现和提出本节课所要研究的问题的?
(2)探索公式二~公式四,我们经历了怎样的过程?用了哪些方法?
(3)运用公式二~公式四将任意角的三角函数化归为锐角的三角函数的基本步骤是怎样的?
(4)你认为还有哪种对称关系值得研究?
师生活动:学生给出答案,发表看法,教师在学生回答的基础上进行适当归纳.
设计意图:(1)回顾从“角的终边相同”时三角函数的关系,到“角的终边具有特殊对称性”的三角函数的关系,进一步落实发现和提出问题的能力,帮助学生建立借助单位圆研究三角函数性质的思维习惯.
(2)通过回顾进一步明确诱导公式的研究路径和运用步骤.
(3)为接下来探究角的终边关于直角坐标系中特殊直线对称的问题留下伏笔.
目标检测设计
1、计算:(1)cos(-420°); (2)sin![]() ; (3)tan(-1 140°).
; (3)tan(-1 140°).
答案:(1)![]() ;(2)
;(2)![]() ;(3)-
;(3)-![]() .
.
2、化简:![]()
答案:![]() .
.
设计意图:检测学生恰当选择公式进行三角函数化简、求值的掌握情况.
布置作业:
1.人教A版教材必修第一册教科书P191练习1(1)(2)(3),2(4)(5)(6),3(2),4;
2.人教A版教材必修第一册教科书习题5.3第1,2,3题
人教A版 (2019)必修 第一册5.3 诱导公式教案设计: 这是一份人教A版 (2019)必修 第一册5.3 诱导公式教案设计,共18页。教案主要包含了知识点框架,例题练习,课后巩固等内容,欢迎下载使用。
【小单元教案】高中数学人教A版(2019)必修第一册--5.6.1 函数y=Asin(wx b)的图象(第1课时)(课时教学设计): 这是一份【小单元教案】高中数学人教A版(2019)必修第一册--5.6.1 函数y=Asin(wx b)的图象(第1课时)(课时教学设计),共3页。
人教A版 (2019)必修 第一册5.3 诱导公式精品第2课时教学设计: 这是一份人教A版 (2019)必修 第一册5.3 诱导公式精品第2课时教学设计,共6页。教案主要包含了六.等内容,欢迎下载使用。