八年级上册1 函数精品教案

4．1　函　数

1．掌握函数的概念以及表示方法；(重点)

2．会求函数的值，并确定自变量的取值范围．(难点)

一、情境导入

在学习与生活中，经常要研究一些数量关系，先看下面的问题．如图是某地一天内的气温变化图．

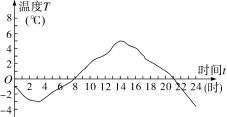
从图中我们可以看到，随着时间t(时)的变化，相应地气温T(℃)也随之变化．那么在生活中是否还有其他类似的数量关系呢？

二、合作探究

探究点一：函数的有关概念

【类型一】 函数的识别

下列关系式中哪些是函数，哪些不是？

(1)y＝x；(2)y＝x2＋z；(3)y2＝x；(4)y＝±.

解析：要判断一个关系式是不是函数，首先看这个变化过程中是否只有两个变量，其次看每一个x的值是否对应唯一确定的y值．

解：(1)此关系式只有两个变量，且每一个x值对应唯一的一个y值，故它是函数．

(2)此关系式中有三个变量，因此y不是x的函数．

(3)此关系式中虽然只有两个变量，但对于每一个确定的x值(x>0)对应的都有2个y值，如当x＝4时，y＝±2，故它不是函数．

(4)对于每个确定的x值(x>0)对应的都有2个y值，如当x＝9时，y＝±3，故它不是函数．

方法总结：由函数的定义可知在某个变化过程中，有两个变量x和y，对于每一个确定的x值，y值都有且只有一个值与之对应，当x值取不同的值时，y的值可以相等也可以不相等，但如果一个x的值对应着两个不同的y值，那么y一定不是x的函数．根据这一点，我们可以判定一个关系式是否表示函数．

【类型二】 自变量的取值范围

函数y＝的自变量x的取值范围是(　　)

A．x≠1  B．x≥－1

C．x>－1  D．一切实数

解析：要使y＝有意义，则必须满足x＋1≥0，∴x≥－1.故选B.

方法总结：求自变量的取值范围应从两个方面考虑：一是必须使含自变量的代数式有意义，二是满足实际问题．

探究点二：函数的关系式及函数值

【类型一】 函数的三种表示方法

近年来，我国西南部分省市遭遇了严重干旱．某水库的蓄水量随着时间的增加而减小，干旱持续时间t(天)与蓄水量V(万立方米)的变化情况如图所示，根据图象回答问题．

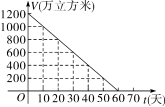
(1)这个图象反映了哪两个变量之间的关系？

(2)根据图象填表：

(3)当t取0至60天之间的任一值时，对应几个V值？

(4)V可以看成t的函数吗？如果是，试写出用自变量表示函数的式子．

解析：(1)通过读图可知，横坐标表示干旱持续时间，纵坐标表示蓄水量，因此它表示的是干旱持续时间与水库蓄水量之间的关系；

(2)根据图象信息确定每个特殊点的坐标即可；

(3)观察图象可得；

(4)可根据函数的定义来判断．

解：(1)图象反映了干旱持续时间与水库蓄水量之间的关系；

(2)如下表：

　　(3)当t取0至60天之间的任一值时，对应着一个V值；

(4)V是t的函数．

根据图象可知，该水库初始蓄水量为1200万立方米，干旱每持续10天，蓄水量减少200万立方米，由此写出的式子为：V＝1200－t＝－20t＋1200(0≤t≤60)．

方法总结：三种函数表示方法之间有互补性，是可以相互转化的．

【类型二】 求函数值

求当x＝－4时的函数值．

(1)y＝；(2)y＝.

解析：利用已知x的值，代入关系式求出即可．

解：(1)代入x＝－4，得y＝＝－；

(2)代入x＝－4，得y＝＝－.

方法总结：利用函数值的定义，正确代入自变量的取值求解是解题的关键．

探究点三：函数的图象

洗衣机在洗涤衣服时，每浆洗一遍都经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水)．在这三个过程中，洗衣机内的水量y(升)与浆洗一遍的时间x(分)之间函数关系的图象大致为(　　)

解析：∵洗衣机工作前洗衣机内无水，∴A，B两选项不正确，淘汰；又∵洗衣机最后排完水，∴D选项不正确，淘汰，所以选项C正确，故选C.

方法总结：本题考查了对函数图象的理解能力，看函数图象要理解两个变量的变化情况．

三、板书设计

函数

在教学过程中，注意通过对以前学过的“变量之间的关系”的回顾与思考，力求提供生动有趣的问题情境，激发学生的学习兴趣，并通过层层深入的问题设计，引导学生进行观察、操作、交流、归纳等数学活动．在活动中归纳、概括出函数的概念，并通过师生交流、生生交流、辨析识别等加深学生对函数概念的理解．