








初中数学湘教版九年级上册2.1 一元二次方程精品教学ppt课件
展开2.1 一元二次方程
湘教版数学九年级上册
会分析实际问题中的数量关系并建立一元二次方程模型,体会建模思想.(难点)
1
2
3
通过实例,理解一元二次方程的概念.
会把一元二次方程化成一般形式,能写出一般形式的各项系数. (重点)
学习目标
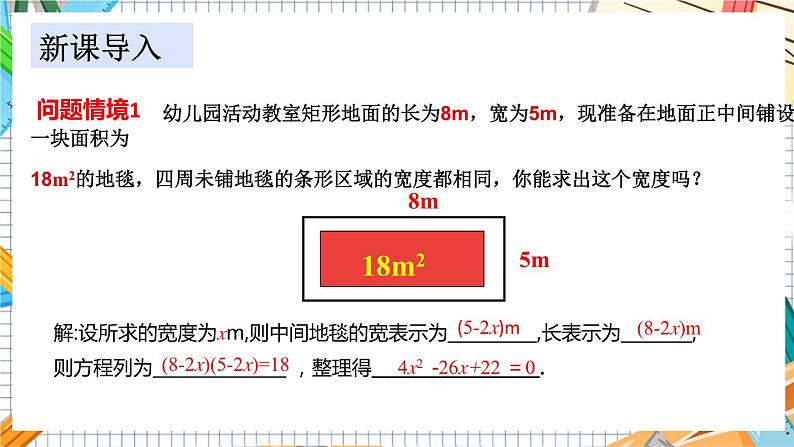
18m2
幼儿园活动教室矩形地面的长为8m,宽为5m,现准备在地面正中间铺设一块面积为18m2的地毯,四周未铺地毯的条形区域的宽度都相同,你能求出这个宽度吗?
8m
问题情境1
解:设所求的宽度为xm,则中间地毯的宽表示为__________,长表示为________,则方程列为_______________ ,整理得_________________.
(5-2x)m
(8-2x)m
(8-2x)(5-2x)=18
4x2 -26x+22 =0
5m
新课导入
桌上有一张矩形纸片,长25cm,宽15cm,在它的四角各剪去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的无盖方盒的底面积为300cm2,那么纸片各角应剪去的正方形边长为多少厘米?
变式:
15㎝
25㎝
(25-2x)(15-2x )= 300,
300cm2
4x2 -8x+75 =0.
解:设剪去的正方形边长为x cm,则无盖方盒的底面的长为(25-2x) cm ,宽为( 15-2x ) cm ,根据题意,可列方程为
整理得
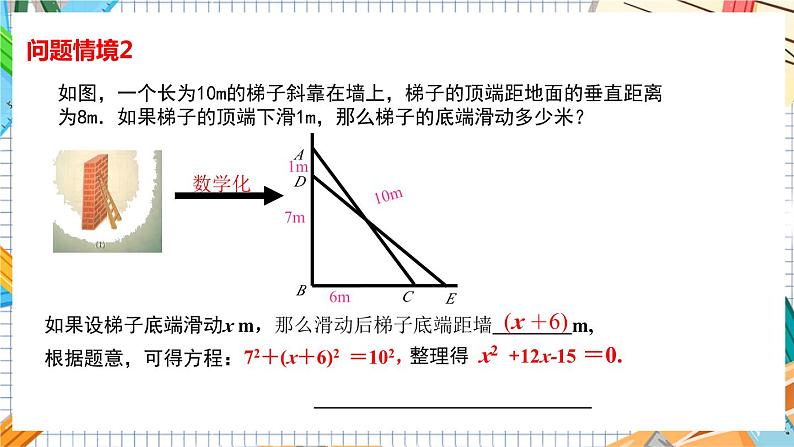
7m
如果设梯子底端滑动x m,那么滑动后梯子底端距墙 m,
根据题意,可得方程:
72+(x+6)2 =102,
(x +6)
如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
10m
问题情境2
A
B
C
1m
D
E
整理得 x2 +12x-15 =0.
6m
要组织一次排球邀请赛,参赛的每两队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参加比赛?
分析:
全部比赛共
4×7=28场.
设应邀请x个队参赛,每个队要与其他 个队各赛1场,
由于甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛,所以全部比赛共 场.
即
(x-1)
问题情境3
思考探究
这四个方程都不是一元一次方程.那么这两个方程与一元一次方程的区别在哪里?它们有什么共同特点呢?
特点:
①都是整式方程(方程两边的分母中不能含有未知数);
②只含一个未知数;
③未知数的最高次数是2.
4x2 -26x+22 =0
4x2 -8x+75 =0
x2 +12x-15 =0
★ 一元二次方程的概念
如果一个方程通过整理可以使右边为0,而左边是只含有一个未知数的二次多项式,这样的方程叫做一元二次方程.
(1) 只含一个未知数;
(2) 是二次多项式
满足的条件:
知识讲解
★ 一元二次方程的一般形式
想一想
为什么要限制a ≠0 , b, c可以为零吗?
a x 2 + b x + c = 0
(a ≠ 0)
二次项系数
一次项系数
常数项
二次项
一次项
当 a = 0 时
bx+c = 0
当 a ≠ 0 , b = 0时
ax2+c = 0
当 a ≠ 0 , c = 0时
ax2+bx = 0
当 a ≠ 0 ,b = c =0时
ax2 = 0
总结:若ax2+bx+c=0是一元二次方程只要满足a ≠ 0 ,b , c 可以为任意实数.
为什么一般形式ax2+bx+c=0中要限制a≠0,b、c 可以为零呢?
当b ≠ 0时,为一元一次方程
一元二次方程
下列方程中哪些是一元二次方程?
是分式
(8) =0
(7)4 - 7x2=0
(6)x2+2x-3=1+x2
例1
(1)ax2-x=2x2;
(2)(a-1)x ∣ a ∣ +1 -2x-7=0.
解:(1)将方程转化为一般形式,得(a-2)x2-x=0,所以当a-2≠0,即a≠2时,原方程是一元二次方程. (2)由∣a ∣+1 =2,且a-1 ≠0知,当a=-1时,原方程是一元二次方程.
总结:用一元二次方程的定义求字母的值的方法:根据未知数的最高次数等于2,列出关于某个字母的方程,再排除使二次项系数等于0的字母的值.
解:去括号,得
3x2-3x=5x+10.
移项、合并同类项,得一元二次方程的一般形式为
3x2-8x-10=0.
其中二次项是3x2,系数是3;一次项是-8x,系数是-8;常数项是-10.
注意:(1)一元二次方程的二次项、二次项系数、一次项、一次项系数、常数项等都是针对一般形式而言的;(2)系数和项均包含前面的符号.
1.判断下列是否为一元二次方程?(1)3x²-x=2 ( ) (2)2(x-1)²=3y ( )(3)3x²-2x+5 ( ) ( )(5)(m²+5)x²+7x-1=0 ( )
√
√
×
×
×
随堂训练
2.方程(2a-4)x2 -2bx+a=0, 在什么条件下此方程为一元二次方程?在什么条件下此方程为一元一次方程?
解: 若(2a-4)x2 -2bx+a=0是一元二次方程,则二次项系数不为零,∴2a-4 ≠0,解得a≠2,即当a≠2时, (2a-4)x2 -2bx+a=0是一元二次方程;若(2a-4)x2 -2bx+a=0是一元一次方程,则二次项系数为零,一次项系数不为零,∴2a-4 =0且-2b ≠0,解得a=2,b≠0,即当a=2,b≠0时, (2a-4)x2 -2bx+a=0是一元一次方程.
3.将下列一元二次方程化成一般形式,并指出它们的二次项系数、一次项系数、常数项分别是多少:
(1) 2x2=3x-1;(2)(x+2)(x-2)-2x(x-1)=0.
解:(1) 2x2=3x-1化为一般形式为 2x2-3x+1=0,∴ 二次项系数、一次项系数、常数项分别是2,-3,1.
(2)(x+2)(x-2)-2x(x-1)=0化为一般形式为 -x2+2x-4=0, ∴ 二次项系数、一次项系数、常数项分别是-1,2,-4.
4.(只列方程)三个连续整数两两相乘,再求和,结果为242,这三个数分别是多少?
解:设第一个数为x,则另两个数分别为x+1, x+2,依题意得方程:
x (x +1) + x(x +2) + (x +1) (x +2) =242.
x2 +2x-80=0.
整理得
一元二次方程
概念
只含一个未知数;是二次多项式;
一般形式
对于ax2+bx+c=0 (a ≠0),其中(a≠0)是一元二次方程的必要条件;确定一元二次方程的二次项系数、一次项系数及常数项要先化为一般式
课堂小结
数学九年级上册4.2 正切获奖教学课件ppt: 这是一份数学九年级上册4.2 正切获奖教学课件ppt,文件包含教学课件九上·湘教·42正切pptx、数学九上·湘教·42正切教案docx等2份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
湘教版九年级上册3.3 相似图形精品教学课件ppt: 这是一份湘教版九年级上册3.3 相似图形精品教学课件ppt,文件包含教学课件九上·湘教·33相似图形pptx、数学九上·湘教·33相似图形教案docx等2份课件配套教学资源,其中PPT共37页, 欢迎下载使用。
初中湘教版3.1 比例线段完美版教学课件ppt: 这是一份初中湘教版3.1 比例线段完美版教学课件ppt,文件包含教学课件九上·湘教·312成比例线段pptx、数学九上·湘教·312成比例线段教案docx等2份课件配套教学资源,其中PPT共24页, 欢迎下载使用。













