





七年级下册第八章 二元一次方程组8.4 三元一次方程组的解法同步训练题
展开![]() 第19课 三元一次方程组
第19课 三元一次方程组
![]()
课程标准 |
1.理解三元一次方程(或组)的含义; 2.会解简单的三元一次方程组; 3. 会列三元一次方程组解决有关实际问题. |
![]()
知识点01 三元一次方程及三元一次方程组的概念
1.三元一次方程的定义:
含有 个未知数,并且含有未知数的项的次数都是 的 方程.如x+y-z=1,2a-3b+4c=5等都是三元一次方程.
注意:
(1)三元一次方程的条件:
①是 方程;
②含有 个未知数;
③含未知数的项的最高次数是 次.
(2)三元一次方程的一般形式:ax+by+cz+d=0,其中a、b、c .
2.三元一次方程组的定义:
一般地,由几个一次方程组成,并且含有三个未知数的方程组,叫做三元一次方程组.
注意:
(1)三个方程中不一定每一个方程中都含有三个未知数,只要三个方程共含有三个未知量即可.
(2)在实际问题中含有三个未知数,当这三个未知数同时满足三个相等关系时,可以建立三元一次方程组求解.
知识点02 三元一次方程组的解法
解三元一次方程组的一般步骤
(1)利用代入法或加减法,把方程组中一个方程与另两个方程分别组成两组,消去两组中的同一个未知数,得到关于另外两个未知数的二元一次方程组;
(2)解这个二元一次方程组,求出两个未知数的值;
(3)将求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个一元一次方程;
(4)解这个一元一次方程,求出最后一个未知数的值;
(5)将求得的三个未知数的值用“{”合写在一起.
注意:
(1)解三元一次方程组的基本思路是:通过“代入”或“加减”消元,把“三元”化为“二元”.使解三元一次方程组转化为解二元一次方程组,进而转化为解一元一次方程.其思想方法是:
![]()
(2)有些特殊的方程组可用特殊的消元法,解题时要根据各方程特点寻求其较简单的解法.
知识点03 三元一次方程组的应用
列三元一次方程组解应用题的一般步骤:
1.弄清题意和题目中的数量关系,用字母(如x,y,z)表示题目中的两个(或三个)未知数;
2.找出能够表达应用题全部含义的相等关系;
3.根据这些相等关系列出需要的代数式,从而列出方程并组成方程组;
4.解这个方程组,求出未知数的值;
5.写出答案(包括单位名称).
注意:
(1)解实际应用题必须写“答”,而且在写答案前要根据应用题的实际意义,检查求得的结果是否合理,不符合题意的应该舍去.
(2)“设”、“答”两步,都要写清单位名称,应注意单位是否统一.
(3)一般来说,设几个未知数,就应列出几个方程并组成方程组.
![]()
考法01 三元一次方程及三元一次方程组的概念
【典例1】下列方程组不是三元一次方程组的是( ).
A. B.
B. C.
C. D.
D.
考法02 三元一次方程组的解法
【典例2】若x:y:z=2:7:5,x﹣2y+3z=6,求![]() 的值.
的值.
【即学即练】解方程组
【典例3】已知方程组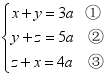 的解使得代数式x-2y+3z的值等于-10,求a的值.
的解使得代数式x-2y+3z的值等于-10,求a的值.
【即学即练】若 ![]() ,则x:y:z= .
,则x:y:z= .
考法03 三元一次方程组的应用
【典例4】小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入2400元;
营业员B:月销售件数300件,月总收入2700元;
假设营业员的月基本工资为x元,销售每件服装奖励y元.
(1)求x、y的值;
(2)若某营业员的月总收入不低于3100元,那么他当月至少要卖服装多少件?
(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需350元;如果购买甲1件,乙2件,丙3件共需370元.某顾客想购买甲、乙、丙各一件共需多少元?
【即学即练】有铅笔、练习本、圆珠笔三种学习用品,若购铅笔3支,练习本7本,圆珠笔1支共需3.15元;若购铅笔4支,练习本8本,圆珠笔2支共需4.2元,那么,购铅笔、练习本、圆珠笔各1件共需( )
A.1.2元 B.1.05元 C.0.95元 D.0.9元
![]()
题组A 基础过关练
1.下列方程组中是三元一次方程组的是( )
A. B.
B. C.
C. D.
D.
2.下列四组数中,是方程组 的解是( )
的解是( )
A. B.
B.![]() C.
C. D.
D.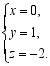
3.三元一次方程组 的解是
的解是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.观察方程组 的系数特征,若要使求解简便,消元的方法应选取( )
的系数特征,若要使求解简便,消元的方法应选取( )
A.先消去![]() B.先消去
B.先消去![]() C.先消去
C.先消去![]() D.以上说法都不对
D.以上说法都不对
5.设![]() ,则
,则![]() 的值为
的值为![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知方程组![]() (xyz≠0),则x:y:z等于( )
(xyz≠0),则x:y:z等于( )
A.2:1:3 B.3:2:1 C.1:2:3 D.3:1:2
8.甲、乙、丙三种商品,若购买甲3件、乙2件、丙1件,共需315元钱,购甲1件、乙2件、丙3件共需285元钱,那么购甲、乙、丙三种商品各一件共需多少钱( )
A.128元 B.130元 C.150 元 D.160元
9.若关于![]() 的方程组
的方程组![]() 的解也是二元一次方程
的解也是二元一次方程![]() 的解,则
的解,则![]() 的值为( )
的值为( )
A.1 B.3 C.![]() D.2
D.2
10.某一长方体纸盒的表面展开图如图所示,根据图中数据可得该长方体纸盒的容积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.某班元旦晚会需要购买甲、乙、丙三种装饰品,若购买甲3件,乙5件,丙1件,共需62元,若购甲4件,乙7件,丙1件共需77元.现在购买甲、乙、丙各一件,共需( )元.A.31 B.32 C.33 D.34
|
|
|
题组B 能力提升练
12.若![]() 是一个三元一次方程,那么
是一个三元一次方程,那么![]() _______,
_______,![]() ________.
________.
13.方程组 的解是_____.
的解是_____.
14.已知|x﹣z+4|+|z﹣2y+1|+|x+y﹣z+1|=0,则x+y+z=________.
15.有甲、乙、丙三种货物,若购买甲3件、乙7件、丙1件,共315元;若购买甲4件、乙10件、丙1件,共420元,现在购买甲、乙、丙各1件,共需_____元.
16.若关于x,y的二元一次方程组![]() 的解也是二元一次方程x+2y=8的解,则k的值为____.
的解也是二元一次方程x+2y=8的解,则k的值为____.
17.重庆市某中学举行全校文艺汇报演出,部分班级需要参与准备工作.这些班级平均每班有36名同学参加,其中参加人数低于30人的班级平均每班有28人参加,参加人数不低于30人的班级平均每班有42人参加.正式开始后,由于工作比较复杂,参与准备工作的班级每个班增加了5人,此时参加人数低于30人的班级平均每班有29人参加,参加人数不低于30人的班级平均每班有45人参加.已知参加的班级个数不低于25,且不高于35,那么参加准备工作的班级共有______个.
18.有一片牧场,草每天都在匀速地生长(即草每天增长的量相等),如果放牧24头牛,则6天吃完牧草;如果放牧21头牛,则8天吃完牧草.设每头牛每天吃草的量是相等的,如果放牧16头牛,则__________天可以吃完牧草.
题组C 培优拔尖练
19.解三元一次方程组 .
.
20.解下列方程组:
(1)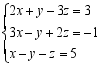 ; (2)
; (2) .
.
21.水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部水果都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
22.阅读材料:
(一)对于方程组 ,每个未知数的系数呈循环对称形式出现,则用以下方法巧解方程组.
,每个未知数的系数呈循环对称形式出现,则用以下方法巧解方程组.
解:将①+②+③,得:![]() ,则
,则![]() …④
…④
用①-④,②-④,③-④,得:![]()
(二)对于方程组![]() 且x,y,z均为正数,因为x,y,z均不为0,则原方程组可改写为
且x,y,z均为正数,因为x,y,z均不为0,则原方程组可改写为 ,每个未知数的次数也是呈循环对称形式出现,则用以下方法巧解方程组.解:将①
,每个未知数的次数也是呈循环对称形式出现,则用以下方法巧解方程组.解:将①![]() ②
②![]() ③,得:
③,得:![]() ,且x,y,z均为正数,则
,且x,y,z均为正数,则![]() ④,
④,
用④![]() ①,④
①,④![]() ②,④
②,④![]() ③,得:
③,得:
利用以上材料,解方程组:
(1) ;
;
(2) ,且a,b,c均为正数.
,且a,b,c均为正数.
23.先阅读材料再回答问题.
对三个数x,y,z,规定![]() ;
;![]() 表示x,y,z这三个数中最小的数,如
表示x,y,z这三个数中最小的数,如![]() ,
,![]()
请用以上材料解决下列问题:
(1)若![]() ,求x的取值范围;
,求x的取值范围;
(2)①若![]() ,求x的值;
,求x的值;
②猜想:若![]() ,那么a,b,c大小关系如何?请直接写出结论;
,那么a,b,c大小关系如何?请直接写出结论;
③问:是否存在非负整数a,b,c使![]() 等式成立?若存在,请求出a,b,c的值;若不存在,请说明理由.
等式成立?若存在,请求出a,b,c的值;若不存在,请说明理由.
初中人教版10.2 直方图精品练习: 这是一份初中人教版10.2 直方图精品练习,文件包含人教版七年级数学下册讲测练第29课直方图教师版doc、人教版七年级数学下册讲测练第29课直方图原卷版doc等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
人教版七年级下册第十章 数据的收集、整理与描述10.1 统计调查优秀同步达标检测题: 这是一份人教版七年级下册第十章 数据的收集、整理与描述10.1 统计调查优秀同步达标检测题,文件包含人教版七年级数学下册讲测练第28课统计调查教师版doc、人教版七年级数学下册讲测练第28课统计调查原卷版doc等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
初中数学人教版七年级下册6.3 实数精品课时训练: 这是一份初中数学人教版七年级下册6.3 实数精品课时训练,文件包含人教版七年级数学下册讲测练第11课实数单元检测教师版doc、人教版七年级数学下册讲测练第11课实数单元检测原卷版doc等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。













