人教版七年级数学下册讲测练 第22课 不等式及其性质（2份打包，原卷版+教师版）
展开
第22课 不等式及其性质
课程标准 |
1．了解不等式的意义，认识不等式和等式都可以用来刻画现实世界中的数量关系. 2. 知道不等式解集的概念并会在数轴上表示解集. 3. 理解不等式的三条基本性质，并会简单应用. |
知识点01 不等式的概念
一般地，用“＜”、 “＞”、“≤”或“≥”表示大小关系的式子，叫做不等式．用“ ”表示不等关系的式子也是不等式．
注意：
(1)不等号“＜”或“＞”表示不等关系，它们具有方向性，不等号的开口所对的数较大．
(2)五种不等号的读法及其意义：
符号 | 读法 | 意义 |
“≠” | 读作“ ” | 它说明两个量之间的关系是不相等的，但不能确定哪个大，哪个小 |
“＜” | 读作“ ” | 表示左边的量比右边的量小 |
“＞” | 读作“ ” | 表示左边的量比右边的量大 |
“≤” | 读作“ ” | 即“不大于”，表示左边的量不大于右边的量 |
“≥” | 读作“ ” | 即“不小于”，表示左边的量不小于右边的量 |
(3)有些不等式中不含未知数，如3＜4，-1＞-2；有些不等式中含有未知数，如2x＞5中，x表示未知数，对于含有未知数的不等式，当未知数取某些值时，不等式的左、右两边符合不等号所表示的大小关系，我们说不等式成立，否则，不等式不成立．
知识点02 不等式的解及解集
1.不等式的解：
能使 的未知数的值，叫做不等式的解。
2.不等式的解集：
对于一个含有未知数的不等式，它的所有解组成这个不等式的 ．
注意：
不等式的解 | 是 的未知数的值，不是一个范围 |
不等式的解集 | 是一个集合，是一个 ．其含义： ①解集中的每一个数值都能使不等式成立； ②能够使不等式成立的所有数值都在解集中 |
3.不等式的解集的表示方法
（1）用最简的不等式表示:一般地，一个含有未知数的不等式有 个解，其解集是一个范围，这个范围可用最简单的不等式来表示．如：不等式x-2≤6的解集为x≤8．
(2)用数轴表示:不等式的解集可以在数轴上直观地表示出来，形象地表明不等式的无限个解．如图所示：
注意：
借助数轴可以将不等式的解集直观地表示出来，在应用数轴表示不等式的解集时，要注意两个“确定”：
一是确定“边界点”，若边界点是不等式的解，则用 ，若边界点不是不等式的解，则用 ；二是确定方向，对边界点a而言，x＞a或x≥a向 画；对边界点a而言，x＜a或x≤a向 画．
注意：在表示a的点上画空心圆圈，表示不包括这一点．
知识点03 不等式的基本性质
不等式的基本性质1：不等式两边加(或减) (或 )，不等号的方向 ．
用式子表示：如果a＞b，那么 ．
不等式的基本性质2：不等式两边都乘(或除以) 数，不等号的方向 ．
用式子表示：如果a＞b，c＞0，那么 (或 )．
不等式的基本性质3：不等式两边乘(或除以) ，不等号的方向 ．
用式子表示：如果a＞b，c＜0，那么 (或 )．
注意：
不等式的基本性质的掌握应注意以下几点：
(1)不等式的基本性质是对不等式变形的重要依据，是学习不等式的基础，它与等式的两条性质既有联系，又有区别，注意总结、比较、体会．
(2)运用不等式的性质对不等式进行变形时，要特别注意性质2和性质3的区别，在乘(或除以)同一个数时，必须先弄清这个数是正数还是负数，如果是负数，不等号的方向要改变．
考法01 不等式的概念
【典例1】有数颗等重的糖果和数个大、小砝码，其中大砝码皆为5克、小砝码皆为1克，且下图是将糖果与砝码放在等臂天平上的两种情形．判断下列正确的情形是 ( )
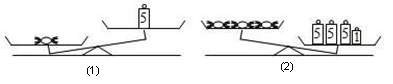
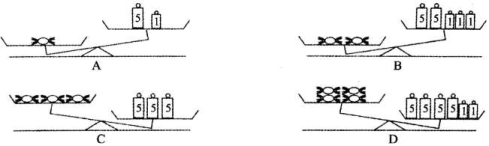
考法02 不等式的解及解集
【典例2】若关于
的不等式x≤a只有三个正整数解，求
的取值范围.
【典例3】如图所示，图中阴影部分表示x的取值范围，则下列表示中正确的是( )
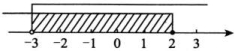
A．-3≤x＜2 B．-3＜x≤2 C．-3≤x≤2 D．-3＜x＜2
【即学即练】根据如图所示的程序计算，若输入x的值为1，则输出y的值为________．
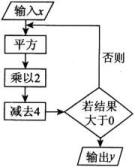
考法03 不等式的基本性质
【典例4】若关于x、y的二元一次方程组
的解满足x+y＜2，则a的取值范围是________．
【即学即练】若关于x的不等式（1﹣a）x＞3可化为
，则a的取值范围是 ．
【即学即练】a、b是有理数，下列各式中成立的是( )．
A．若a＞b，则a2＞b2； B．若a2＞b2，则a＞b
C．若a≠b，则｜a｜≠|b| D．若｜a｜≠|b|，则a≠b
题组A 基础过关练
1．式子：①2＞0；②4x＋y≤1；③x＋3＝0；④y－7；⑤m－2.5＞3.其中不等式有( )
A．1个 B．2个 C．3个 D．4个
2．若m＞n，则下列不等式正确的是（ ）
A．m﹣2＜n﹣2 B．
C．6m＜6n D．﹣8m＞﹣8n
3．下面列出的不等式中，正确的是（ ）
A．“m不是正数”表示为m＜0
B．“m不大于3”表示为m＜3
C．“n与4的差是负数”表示为n﹣4＜0
D．“n不等于6”表示为n＞6
4．若
是关于x的一元一次不等式，则m的值为( )
A．±1 B．1 C．－1 D．0
5．下列不等式变形正确的是（ ）
A．由
，得
B．由，得
C．由，得
D．由，得
6．下列数值中不是不等式5x≥2x＋9的解的是( )
A．5 B．4 C．3 D．2
7．不等式x＜－2的解集在数轴上表示为( )
A．
B．
C．
D．
8．若不等式
的解集是
，则
必满足（ ）
A．
B．
C．
D．
9．用不等式表示图中的解集，其中正确的是（ ）
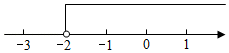
A．x≥﹣2 B．x≤﹣2 C．x＜﹣2 D．x＞﹣2
10．如果(m+3)x＞2m+6的解集为x＜2，则m的取值范围是( )
A．
B．
C．
D．m是任意实数
题组B 能力提升练
11．“x的3倍与2的差不大于-1”所对应的不等式是___________.
12．“5与m的2倍的和是负数”可以用不等式表示为_____．
13．用不等式表示下列各语句所描述的不等关系：
（1）
是正数：_____________________；
（2）
是负数：_____________________；
（3）
不小于4：_____________________；
（4）
是非负数：_____________________；
（5）的2倍比9大：_____________________；
（6）
的一半与8的和是负数：_____________________；
（7）
的3倍与5的和大于的
：_____________________；
（8）
相反数是非正数：_____________________；
14．一种药品的说明书上写着：“每日用量60~120mg，分4次服用”，一次服用这种药量x(mg)范围为_________．
15．如图所示的不等式的解集是________．
16．若5x3m-2-2＞7是一元一次不等式，则m=_____．
17．如果不等式(a－3)x＜b的解集是x>
，那么a的取值范围是________.
18．对于一个数，我们用
表示小于的最大整数 ，例如：
，
，如果
，则的取值范围为__________．
题组C 培优拔尖练
19．在数轴上表示下列不等式的解集：
(1)x＞3
(2)x≥－2
(3)x≤4
(4)x＜－
20．用适当的不等式表示下列不等关系：
（1）x减去6大于12；
（2）x的2倍与5的差是负数；
（3）x的3倍与4的和是非负数；
（4）y的5倍与9的差不大于
；
21．用不等式表示
（1）a的
与一1的差是非正数．
（2）a的平方减去b的立方大于a与b的和．
（3）a的
减去4的差不小于-6．
（4）x的2倍与y的和不大于5．
（5）长方形的长与宽分别为4、
，它的周长大于20．
22．不等式的解集中是否一定有无限多个数？
不等式|x|≤0、x2＜0的解集是什么？
不等式x2＞0和x2+4＞0的解集分别又是什么？
