




初中数学华师大版九年级下册第26章 二次函数26.1 二次函数作业课件ppt
展开一、选择题1. [2021吉林长春期中]将抛物线y=2x2向上平移3个单位,再向右平移2个单位,所得到的抛物线为( ) A.y=2(x+2)2+3B.y=2(x-2)2+3C.y=2(x-2)2-3D.y=2(x+2)2-3
2. [2021辽宁沈阳二模]已知抛物线y=-x2+bx+4经过(-2,n)和(4,n)两点,则n的值为 ( )A.-2B.-4C.2D.4
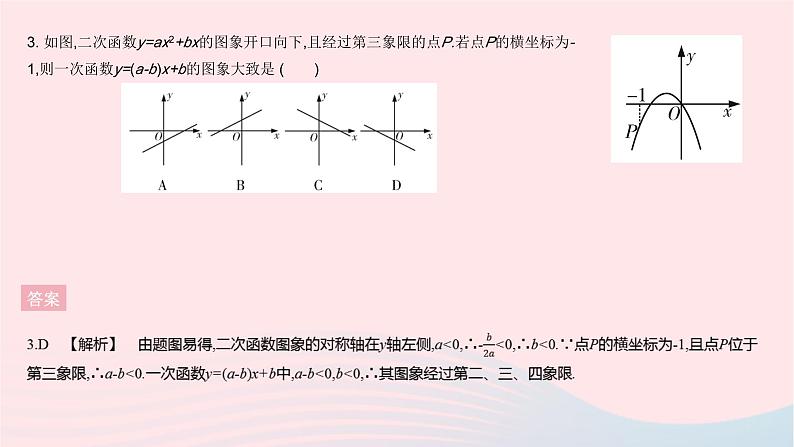
3. 如图,二次函数y=ax2+bx的图象开口向下,且经过第三象限的点P.若点P的横坐标为-1,则一次函数y=(a-b)x+b的图象大致是 ( )
4. 已知二次函数y=ax2+2ax+a+2a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且当-2≤x≤1时,y的最大值为9,则a的值为 ( )A.-1B.1C.-2D.2
4.B 【解析】 ∵二次函数y=ax2+2ax+a+2a2+3=a(x+1)2+2a2+3(其中x是自变量),∴该函数的图象的对称轴为直线x=-1.∵当x≥2时,y随x的增大而增大,∴a>0.∵当-2≤x≤1时,y的最大值为9,∴x=1时,y=9,∴9=a(1+1)2+2a2+3,解得a1=-3(舍去),a2=1.综上可得,a的值是1.
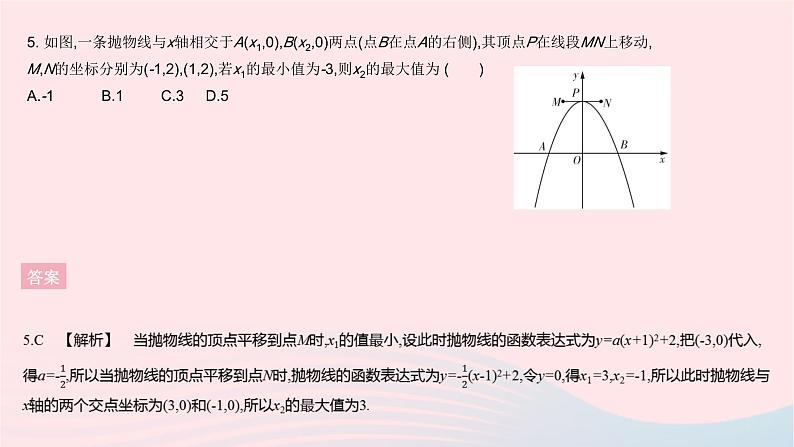
5. 如图,一条抛物线与x轴相交于A(x1,0),B(x2,0)两点(点B在点A的右侧),其顶点P在线段MN上移动,M,N的坐标分别为(-1,2),(1,2),若x1的最小值为-3,则x2的最大值为 ( )A.-1 B.1 C.3D.5
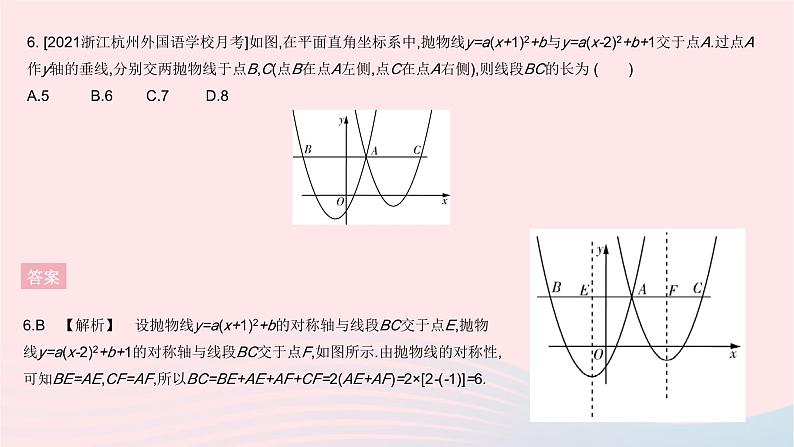
6. [2021浙江杭州外国语学校月考]如图,在平面直角坐标系中,抛物线y=a(x+1)2+b与y=a(x-2)2+b+1交于点A.过点A作y轴的垂线,分别交两抛物线于点B,C(点B在点A左侧,点C在点A右侧),则线段BC的长为 ( )A.5 B.6C.7D.8
6.B 【解析】 设抛物线y=a(x+1)2+b的对称轴与线段BC交于点E,抛物线y=a(x-2)2+b+1的对称轴与线段BC交于点F,如图所示.由抛物线的对称性,可知BE=AE,CF=AF,所以BC=BE+AE+AF+CF=2(AE+AF)=2×[2-(-1)]=6.
8. [2020四川泸州中考]已知二次函数y=x2-2bx+2b2-4c(其中x是自变量)的图象经过不同两点A(1-b,m),B(2b+c,m),且该二次函数的图象与x轴有公共点,则b+c的值为 ( )A.-1B.2C.3D.4
10. 已知抛物线y=ax2+bx+c(a,b,c为常数,a≠0)经过点(-1,0),(0,3),其对称轴在y轴右侧,给出下列结论:①抛物线经过点(1,0);②方程ax2+bx+c=2有两个不相等的实数根;③-3
14. 某班数学兴趣小组对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下: 其中,m= . (2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.(3)观察函数图象,写出两条函数的性质.(4)进一步探究函数图象发现:①函数图象与x轴有 个交点,所以对应的方程x2-2|x|=0有 个实数根; ②方程x2-2|x|=2有 个实数根; ③关于x的方程x2-2|x|=a有4个实数根时,a的取值范围是 .
14. 【解析】 (1)0(2)如图所示.(3)函数的最小值为-1,函数图象关于y轴对称.(可从函数的最值、增减性、图象的对称性等方面阐述.答案不唯一,合理即可)(4)①3 3;②2;③-1
16. 如图,已知抛物线y1=x2+mx与抛物线y2=ax2+bx+c的形状相同,开口方向相反,且相交于点A(-3,-6)和点B(1,6).抛物线y2与x轴的正半轴交于点C,P为抛物线y2上A,B两点间的一动点,过点P作PQ∥y轴,与y1交于点Q,与x轴交于点G.(1)求抛物线y1与抛物线y2的函数表达式.(2)四边形APBQ的面积为S,求S的最大值,并写出此时点P的坐标.(3)y2的对称轴为直线l,l与PC交于点E,与x轴交于点M,在(2)的条件下,直线l上是否存在一点T,使得以T,E,C为顶点的三角形与△APQ相似?如果存在,求出点T的坐标;如果不存在,请说明理由.
人教版九年级下册29.1 投影作业课件ppt: 这是一份人教版九年级下册29.1 投影作业课件ppt,共12页。PPT课件主要包含了易错分析等内容,欢迎下载使用。
华师大版九年级下册26.1 二次函数作业ppt课件: 这是一份华师大版九年级下册26.1 二次函数作业ppt课件,共11页。
华师大版九年级上册24.4 解直角三角形作业ppt课件: 这是一份华师大版九年级上册24.4 解直角三角形作业ppt课件,共28页。













