华师大版九年级下册26.1 二次函数精品教学课件ppt

这是一份华师大版九年级下册26.1 二次函数精品教学课件ppt，文件包含261二次函数课件ppt、261二次函数教学设计doc等2份课件配套教学资源，其中PPT共23页， 欢迎下载使用。

请同学们欣赏下面的图片
这些图形有什么共同特点呢？
1、亲爱的同学们，回想一下，什么是函数？2、我们学过哪些函数，函数的解析式还记得吗？
在某变化过程中的两个变量x、y，当变量x在某个范围内取一个 确定的值，另一个变量y总有唯一的值与它对应。 这样的两个变量之间的关系我们把它叫做函数关系。
一次函数y=kx+b (k≠0)
正比例函数y=kx(k≠0)
2、我们学过哪些函数，函数的解析式还记得吗？
要用总长为20米的铁栏杆，一面靠墙，围成一个矩形的花圃。怎样围法，才能使围成的面积最大？
活动探究：思考以下问题，动手做一做。（小组讨论，3min）
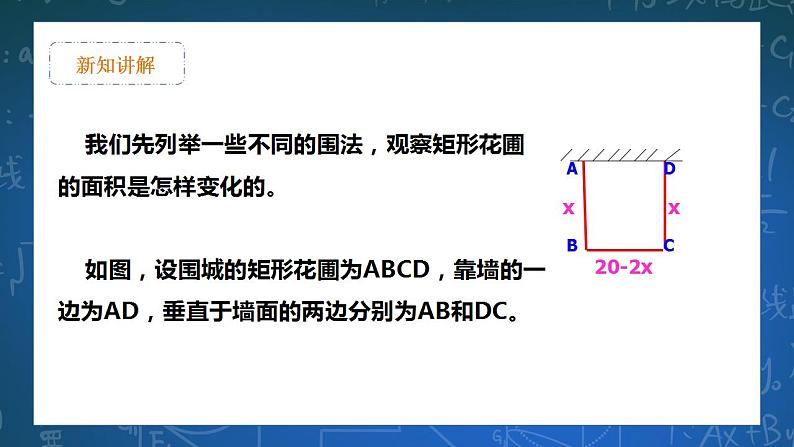
我们先列举一些不同的围法，观察矩形花圃的面积是怎样变化的。 如图，设围城的矩形花圃为ABCD，靠墙的一边为AD，垂直于墙面的两边分别为AB和DC。
从所填的表格中，你能发现什么？能做出怎样的猜想？
给出矩形一边AB长的一些值（0＜AB＜10），可以求出BC的长，从而可得矩形的面积。试将计算结果填入下表的空白处：
分析：我们看到，对于一边AB长的每一个确定值（0＜AB＜10），矩形的面积有唯一确定的值与它对应。也就是说，面积是一边AB长的函数。
当变量AB的长取何值时，矩形面积的值最大？为此，先求出这个函数关系式。设AB的长为xm，矩形的面积为ym2，y是x的函数。试写出这个函数关系式。
y=x(20-2x) (0﹤x﹤10)即： y=-2x2+20x (0﹤x﹤10)
某商店将每商品进价为8元的商品按每10元出售，一天可售出100件。该店想通过降低售价、增加销售量的办法来提高利润。经市场调查，发现这种商品单价每降低0.1元，其销售量可增加约10件。将这种商品的售价降低多少时，能使销售利润最大？
销售利润=（售价-进价）×销售量
分析 在这个问题中，销售商品的利润与其降价的数量有关。设每件商品降低x元（0≤x≤2），销售该商品每天的利润为y元，则y是x的函数。
为什么要限定0≤x≤2 ？
当x取何值时，函数取得最大值？ 为此，我们先求出这个函数关系式。
由上面两个问题的分析，我们可以得到：问题1中的函数关系式为 y=x(20-2x) (0﹤x﹤10)即： y=-2x2+20x (0﹤x﹤10)问题2中的函数关系式为y=(10-x-8)(100+100x) ( 0≤x≤2)即: y=-100x2+100x+200 ( 0≤x≤2)
探索 观察所得的两个函数关系式，它们有什么共同特点？
定义：形如y=ax2+bx+c (a,b,c是常数，a≠0)的函数叫做x的二次函数。 a为二次项系数，b为一次项系数，c为常数项
注意 1、 y=ax2+bx+c 等式右边关于自变量x的代数式一定是整式。 （a,b,c为常数，且a≠0，b,c可为0） (1)y=ax² --------- (a≠0,b=0,c=0,). (2)y=ax²+c ------ (a≠0,b=0,c≠0). (3)y=ax²+bx ---- (a≠0,b≠0,c=0).2 、等式的右边自变量x最高次数为2，可以没有一次项和常数项，但不能没有二次项。3、抛开实际问题，自变量x的取值是全体实数。
下列函数中,哪些是二次函数？
(1）y=6(x-2)²+3
(3)y=(x+5)²-x²
判断一个函数是否是二次函数的关键是： 1、二次项的系数(a)是否为0. 2、自变量的最高次数为2. 3、函数关系式的一般式是否为整式.
2、如果函数y=(m-5) +mx+4是二次函数,则m的值一定是______
1、如果函数y= +mx+4 是二次函数,则m的值一定是______
解：由题意得 m2-5m+2=2 解得，m=0或5
解：由题意得 m2-5m+2=2且m-5≠0 ∴ m=0
形如y=ax2+bx+c (a,b,c是常数，a≠0)的函数叫做x的二次函数。
二次项系数不能为0,自变量x的最高次数是二次, ax²+bx+c是整式。
26.1 二次函数1、二次函数的定义2、定义的实质及运用