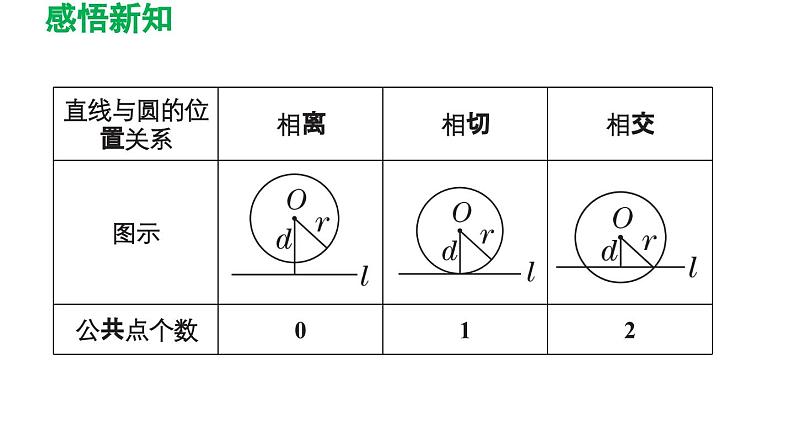
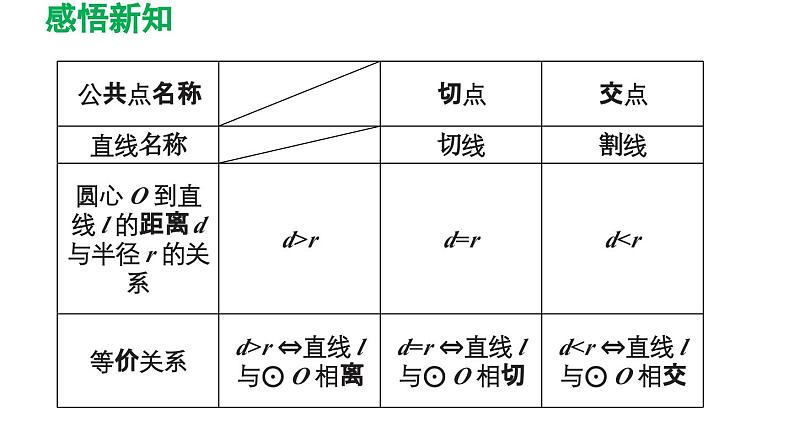
人教版九年级上册24.2.2 直线和圆的位置关系说课ppt课件

这是一份人教版九年级上册24.2.2 直线和圆的位置关系说课ppt课件，共60页。PPT课件主要包含了逐点学练，本节小结，作业提升，学习目标，本节要点，学习流程，感悟新知，知识点，直线与圆的位置关系，－2m2等内容，欢迎下载使用。

直线与圆的位置关系切线的判定切线的性质切线长定理三角形的内切圆
要点提醒如果一条直线满足下列三个条件中的任意两个，那么第三个也成立：1.过圆心；2.过切点；3.垂直于切线 .
如图 24.2-12，在 Rt △ ABC 中，∠ C=90°， AC=6 cm，BC=8 cm，则直线 AB 和以点 C 为圆心， r 为半径的圆有何位置关系？为什么？(1) r=4 cm；(2) r = 4.8 cm；(3) r = 7 cm.
解题秘方：求出点 C 到 AB 的距离，再将其与圆的半径的大小进行比较 .
解：如图24.2-12，过点C作CD⊥ AB于点D.在 Rt △ ABC 中，∠ ACB=90°， AC=6 cm，BC=8 cm，则 AB=10 cm.又∵ AB· CD=AC· BC，∴ CD=4.8 cm.(1)当 r =4 cm 时， CD ﹥ r，直线 AB 和⊙ C 相离；(2)当 r =4.8 cm 时， CD=r，直线 AB 和⊙ C 相切；(3)当 r =7 cm 时， CD < r，直线 AB 和⊙ C 相交 .
1-1. [ 中考·嘉兴 ] 已知平面内有⊙ O和点A， B，若⊙ O半径为2cm，线段OA=3 cm， OB=2 cm，则直线 AB 与⊙ O 的位置关系为( )A. 相离 B. 相交C. 相切 D. 相交或相切
如图 24.2－ 13， 在 △ ABC 中， ∠ C=90 °，∠ A=30°， O 是 AB 上的一点， OB=m ( m>0 ) ，⊙ O 的半径 r 为 12 ，当 m 分别在什么范围内取值时，直线 BC 与⊙ O相离、相切、相交？
解题秘方：利用直线与圆的位置关系的性质建立方程(或不等式)求 m 的取值范围 .
解：如图 24. 2 － 13，作 OD ⊥ BC 于点 D.∵∠ A=30°，∠ C=90°，∴∠ B=60° .∴∠ DOB=30° .
2-1.已知直线 l 与半径为 2 的 ⊙ O 的位置关系是相离，则点 O 到直线 l 的距离的取值范围在数轴上表示正确的是( )
2-2. (易错题)在平面直角坐标系中，⊙ M 的圆心坐标为( m， 4) ， 半径是2，如果⊙ M 与y 轴相切 , 那么 m=_______ ；如果 ⊙ M 与 y轴相交 , 那么 m的取 值范围是__________ .
1.判定定理 经过半径的外端并且垂直于这条半径的直线是圆的切线 .
特别提醒 切线必须同时具备两个条件：1.直线过半径的外端；2.直线垂直于这条半径.
2. 判定方法 (1)定义法： 与圆有唯一公共点的直线是圆的切线；(2)数量法： 圆心到直线的距离等于半径的直线是圆的切线；(3)判定定理法： 经过半径的外端并且垂直于这条半径的直线是圆的切线 .
解题秘方：利用“有切点，连半径，证垂直”判定圆的切线 .
3-1.如图，点 C 是⊙ O上 的 一 点， AB 是 ⊙ O的直径，∠ CAB=∠ DCB，那么 CD 与⊙ O 的位置关系是( )A. 相交 B. 相离C. 相切 D. 相交或相切
如图 24.2－15，在 Rt △ ABC 中，∠ B=90°， ∠ BAC的平分线交 BC 于点 D，以点 D 为圆心， DB 长为半径作⊙ D.求证： AC 与⊙ D 相切 .
证明： 如图 24.2－15，过点 D 作 DF ⊥ AC 于点 F.∵∠ B=90°，∴ DB ⊥ AB.又∵ AD 平分∠ BAC，∴ DF=DB.∴ AC 与⊙ D 相切 .
解题秘方：利用“无切点，作垂线，证半径”判定圆的切线 .
4-1.如图，点 D 是∠ AOB的 平分线 OC 上任意 一点，过点 D 作 DE ⊥ OB于点 E，以 DE 为半径作⊙ D. 求证： OA 是 ⊙ D的切线．
证明：过点D作DF⊥OA于点F.∵点D是∠AOB的平分线OC上任意一点，DE⊥OB，∴DF＝DE，即点D到直线OA的距离等于⊙D的半径DE.∴OA是⊙D的切线．
1.性质定理 圆的切线垂直于过切点的半径 .
2. 切线的性质 (1)切线和圆只有一个公共点 ；(2)圆心到切线的距离等于半径 ；(3)圆的切线垂直于过切点的半径 ；(4)经过圆心且垂直于切线的直线必过切点(找切点用) ；(5)经过切点且垂直于切线的直线必过圆心(找圆心用) .
特别提醒切线的判定定理与性质定理的区别：切线的判定定理是在未知相切而要证明相切的情况下使用；切线的性质定理是在已知相切而要推得其他的结论时使用.它们是一个互逆的过程，不要混淆.
如图 24.2-16， AB 为⊙ O 的直径， PD 切⊙ O 于点 C，交 AB 的延长线于点 D，且∠ D=2 ∠ CAD.
解题秘方：(1)利用“等半径”得等腰三角形；(2)利用“切线垂直于过切点的半径”构造直角三角形，再结合相关性质求解 .
(1)求∠ D 的度数 .
解：如图 24.2-16，连接 OC.∵ AO=CO，∴∠ OAC= ∠ ACO.∴∠ COD=2 ∠ CAD.又∵∠ D=2 ∠ CAD，∴∠ D= ∠ COD.∵ PD 切⊙ O 于点 C，∴ OC ⊥ PD，即∠ OCD=90° . ∴∠ D=45° .
(2)若 CD=2，求 BD 的长 .
[ 中考·泰安 ] 如图 ，在△ ABC 中， AB=6，以点A 为圆心，3 为半径的圆与边 BC 相切于点 D, 与 AC， AB 分别交于点 E， G，点 F 是优弧 GE 上一点，∠ CDE=18° ，则∠ GFE 的度数是( )A. 50° B. 48° C. 45° D. 36°
[ 中考·湖州 ]如图 24.2-17，已知 BC 是⊙ O 的直径，AC 切⊙ O 于点 C， AB 交⊙ O 于点 D， E 为 AC 的中点，连接 DE.
解题秘方：(1)构造直径所对的圆周角，利用直径所对的圆周角是直角求解；(2)利用“连半径，证垂直”求解 .
(1)若 AD=DB， OC=5，求切线 AC 的长；
解：如图 24.2-17，连接 CD.∵ BC 是⊙ O 的直径，∴∠ BDC=90°，即 CD ⊥ AB.∵ AD=DB，∴ AC=BC=2OC=10.
(2)求证： DE 是⊙ O 的切线 .
6-1. [ 中考·雅安 ] 如图，已知 AB 是⊙ O 的直径，AC， BC 是⊙ O 的弦，OE∥ AC交BC于点E，过点 B 作⊙ O 的切线交OE 的延长线于点 D，连接 DC 并 延 长 交 BA的延长线于点 F．(1)求证： DC 是⊙ O的切线；
证明：连接OC.∵AB是⊙O的直径，∴∠ACB＝90°.∵OE∥AC，∴∠OEB＝∠ACB＝90°.∴OD⊥BC. ∴OD垂直平分BC.∴DB＝DC. ∴∠DBE＝∠DCE.又∵OC＝OB，∴∠OBE＝∠OCE. ∴∠DBO＝∠OCD.
∵DB为⊙O的切线，OB是半径，∴DB⊥OB.∴∠OCD＝∠DBO＝90°.∴OC⊥DC.又∵OC是⊙O的半径，∴DC是⊙O的切线．
(2)若∠ ABC=30°，AB=8，求线段CF 的长.
1.切线长定义 经过圆外一点作圆的切线，这点和切点之间的线段的长，叫作这点到圆的切线长 .
切线是直线，不可度量；切线长是切线上切点与切点外另一点之间的线段的长，可以度量 .
2. 切线长定理从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角 .
特别提醒经过圆上一点作圆的切线，有且只有一条，过切点的半径垂直于这条切线；经过圆外一点作圆的切线，有两条，这点和两个切点所连的两条线段相等.
3. 示例 如图 24.2 － 18 是切线长定理的一个基本图形 , 可以直接得到结论：(1) PO ⊥ AB； (2) AO ⊥ AP， BO ⊥ BP；(3) AP=BP； (4) ∠ 1= ∠ 2= ∠ 3= ∠ 4；(5) AD=BD； (6) AC = BC等 .
如图 24. 2－19， PA， PB， DE 分别切⊙ O 于点 A， B， C，点 D 在 PA 上，点 E 在 PB 上 .
解题秘方：根据切线长的定义，判断出 切线长，再利用切线长定理，找到相等关系 .
(1)若 PA=10，求△ PDE 的周长；
解：∵ PA， PB， DE 分别切⊙ O 于点 A， B， C，∴ PA=PB， DA=DC， EC=EB.∴PD+DE+PE=PD+DA+EB+PE=PA+PB=10+10=20.∴△ PDE 的周长为 20.
(2)若∠ P=50°，求∠ DOE 的度数 .
7-1. (易错题)如图，直线 AB， AD 分别与⊙ O 相切于点 B， D，C 为 ⊙ O 上一点， 且∠ BCD=130°，则∠ A的度数是( )A.70° B.85°C.80° D.100°
如图 24.2－20， PA， PB 是⊙ O 的切线，切点分别为 A，B， BC 为⊙ O 的直径，连接 AB， AC， OP.
解题秘方：活用切线长定理中角的关系结合相关性质求解 .
求证：(1) ∠ APB = 2 ∠ ABC；
证明：∵ BC 是⊙ O 的直径，∴∠ BAC=90°，即 AC ⊥ AB.由(1)知 OP ⊥ AB，∴ AC ∥ OP.
(2) AC ∥ OP.
8-1.如图 ， AB ，BC， CD 分别与⊙ O 相切于点E，F，G， 若∠ BOC=90°，求证： AB ∥ CD.
证明：∵∠BOC＝90°，∴∠OBC＋∠OCB＝90°.又∵BE与BF为⊙O的切线，∴BO为∠EBF的平分线．∴∠OBE＝∠OBC. 同理可得∠OCB＝∠OCG，∴∠OBE＋∠OCG＝∠OBC＋∠OCB＝90°.∴∠OBC＋∠OCB＋∠OBE＋∠OCG＝180°，即∠ABF＋∠DCF＝180°. ∴AB∥CD.
1. 三角形的内切圆 与三角形各边都相切的圆叫作三角形的内切圆，这个三角形叫作圆的外切三角形 .
要点解读●一个三角形有且只有一个内切圆，而一个圆有无数个外切三角形 .●三角形的内心在三角形的内部.
2. 三角形的内心 三角形的内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心.3. 三角形内心的性质 三角形的内心到三角形三条边的距离相等，且等于其内切圆的半径.
王奶奶有一块三角形的布料 ABC，∠ ACB=90°，她要裁剪一个圆片，已知 AC=60 cm， BC=80 cm. 为了充分地利用这块布料，使裁剪下来的圆片的直径尽量大些，她应该怎样裁剪？这个圆片的半径是多少？
解题秘方：在三角形中裁剪下的最大圆就是这个三角形的内切圆 .
解： 如图 24.2-21，设△ ABC 的内切圆⊙ O 的半径为 r cm，⊙ O 分别切 AB， BC， AC 于点 D， E， F，连接 OE， OF，则四边形 OECF 为正方形 .
直角三角形内切圆的半径等于两直角边的和减去斜边之差的一半.
9-1.如图， ⊙ O 是△ ABC 的内切圆，切点分别为 D， E， F.(1)若 AB=9， BC=14， AC=13， 求 AD，BE， CF 的长；(2)若 BA=BC=13，AC=24， 求 △ ABC 的内切圆的半径 .
解：(1)设AD＝x，BE＝y，CF＝z，由切线长定理可得 AD＝AF＝x，BD＝BE＝y，CE＝CF＝z.∴x＋y＝9，y＋z＝14，x＋z＝13，解得x＝4，y＝5，z＝9.即AD＝4，BE＝5，CF＝9.
如图 24.2 － 22， 在 △ ABC 中， ∠ A=70 °， 点 O 是△ ABC 的内心，求∠ BOC 的度数 .
解题秘方：三角形的内心是三角形三个内角的平分线的交点 .
10-1. [ 中考· 湖州 ] 如图， 已知 △ ABC 的内切圆 ⊙ O 与 BC 边 相切于点 D， 连接 OB，OD. 若 ∠ ABC=40°，则 ∠ BOD 的度数是_______．